Adaptive Consensus Gradients Aggregation for Scaled Distributed Training

Distributed machine learning has recently become a critical paradigm for training large models on vast datasets. We examine the stochastic optimization problem for deep learning within synchronous parallel computing environments under communication constraints. While averaging distributed gradients is the most widely used method for gradient estimation, whether this is the optimal strategy remains an open question. In this work, we analyze the distributed gradient aggregation process through the lens of subspace optimization. By formulating the aggregation problem as an objective-aware subspace optimization problem, we derive an efficient weighting scheme for gradients, guided by subspace coefficients. We further introduce subspace momentum to accelerate convergence while maintaining statistical unbiasedness in the aggregation. Our method demonstrates improved performance over the ubiquitous gradient averaging on multiple MLPerf tasks while remaining extremely efficient in both communicational and computational complexity.

Accelerating Error Correction Code Transformers

Error correction codes (ECC) are crucial for ensuring reliable information transmission in communication systems. Choukroun & Wolf (2022b) recently introduced the Error Correction Code Transformer (ECCT), which has demonstrated promising performance across various transmission channels and families of codes. However, its high computational and memory demands limit its practical applications compared to traditional decoding algorithms. Achieving effective quantization of the ECCT presents significant challenges due to its inherently small architecture, since existing, very low-precision quantization techniques often lead to performance degradation in compact neural networks. In this paper, we introduce a novel acceleration method for transformer-based decoders. We first propose a ternary weight quantization method specifically designed for the ECCT, inducing a decoder with multiplication-free linear layers. We present an optimized self-attention mechanism to reduce computational complexity via codeaware multi-heads processing. Finally, we provide positional encoding via the Tanner graph eigendecomposition, enabling a richer representation of the graph connectivity. The approach not only matches or surpasses ECCT's performance but also significantly reduces energy consumption, memory footprint, and computational complexity. Our method brings transformer-based error correction closer to practical implementation in resource-constrained environments, achieving a 90% compression ratio and reducing arithmetic operation energy consumption by at least 224 times on modern hardware.

Factor Graph Optimization of Error-Correcting Codes for Belief Propagation Decoding

The design of optimal linear block codes capable of being efficiently decoded is of major concern, especially for short block lengths. As near capacity-approaching codes, Low-Density Parity-Check (LDPC) codes possess several advantages over other families of codes, the most notable being its efficient decoding via Belief Propagation. While many LDPC code design methods exist, the development of efficient sparse codes that meet the constraints of modern short code lengths and accommodate new channel models remains a challenge. In this work, we propose for the first time a data-driven approach for the design of sparse codes. We develop locally optimal codes with respect to Belief Propagation decoding via the learning on the Factor graph (also called the Tanner graph) under channel noise simulations. This is performed via a novel tensor representation of the Belief Propagation algorithm, optimized over finite fields via backpropagation coupled with an efficient line-search method. The proposed approach is shown to outperform the decoding performance of existing popular codes by orders of magnitude and demonstrates the power of data-driven approaches for code design.

Learning Linear Block Error Correction Codes

Error correction codes are a crucial part of the physical communication layer, ensuring the reliable transfer of data over noisy channels. The design of optimal linear block codes capable of being efficiently decoded is of major concern, especially for short block lengths. While neural decoders have recently demonstrated their advantage over classical decoding techniques, the neural design of the codes remains a challenge. In this work, we propose for the first time a unified encoder-decoder training of binary linear block codes. To this end, we adapt the coding setting to support efficient and differentiable training of the code for end-to-end optimization over the order two Galois field. We also propose a novel Transformer model in which the self-attention masking is performed in a differentiable fashion for the efficient backpropagation of the code gradient. Our results show that (i) the proposed decoder outperforms existing neural decoding on conventional codes, (ii) the suggested framework generates codes that outperform the {analogous} conventional codes, and (iii) the codes we developed not only excel with our decoder but also show enhanced performance with traditional decoding techniques.

Reconstructing the Hemodynamic Response Function via a Bimodal Transformer

The relationship between blood flow and neuronal activity is widely recognized, with blood flow frequently serving as a surrogate for neuronal activity in fMRI studies. At the microscopic level, neuronal activity has been shown to influence blood flow in nearby blood vessels. This study introduces the first predictive model that addresses this issue directly at the explicit neuronal population level. Using in vivo recordings in awake mice, we employ a novel spatiotemporal bimodal transformer architecture to infer current blood flow based on both historical blood flow and ongoing spontaneous neuronal activity. Our findings indicate that incorporating neuronal activity significantly enhances the model's ability to predict blood flow values. Through analysis of the model's behavior, we propose hypotheses regarding the largely unexplored nature of the hemodynamic response to neuronal activity.

Deep Quantum Error Correction

Quantum error correction codes (QECC) are a key component for realizing the potential of quantum computing. QECC, as its classical counterpart (ECC), enables the reduction of error rates, by distributing quantum logical information across redundant physical qubits, such that errors can be detected and corrected. In this work, we efficiently train novel deep quantum error decoders. We resolve the quantum measurement collapse by augmenting syndrome decoding to predict an initial estimate of the system noise, which is then refined iteratively through a deep neural network. The logical error rates calculated over finite fields are directly optimized via a differentiable objective, enabling efficient decoding under the constraints imposed by the code. Finally, our architecture is extended to support faulty syndrome measurement, to allow efficient decoding over repeated syndrome sampling. The proposed method demonstrates the power of neural decoders for QECC by achieving state-of-the-art accuracy, outperforming, for a broad range of topological codes, the existing neural and classical decoders, which are often computationally prohibitive.

Denoising Diffusion Error Correction Codes

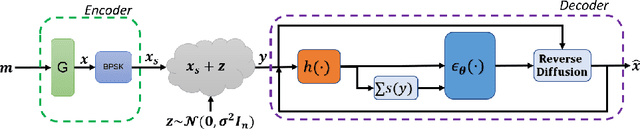
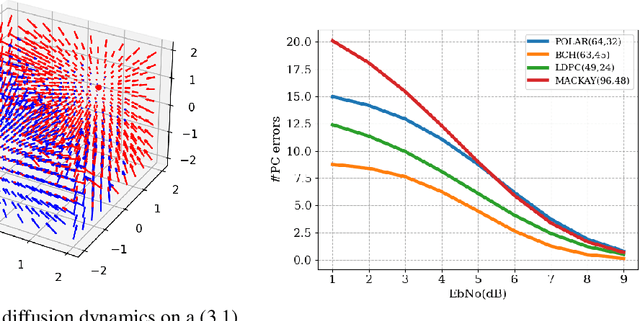
Error correction code (ECC) is an integral part of the physical communication layer, ensuring reliable data transfer over noisy channels. Recently, neural decoders have demonstrated their advantage over classical decoding techniques. However, recent state-of-the-art neural decoders suffer from high complexity and lack the important iterative scheme characteristic of many legacy decoders. In this work, we propose to employ denoising diffusion models for the soft decoding of linear codes at arbitrary block lengths. Our framework models the forward channel corruption as a series of diffusion steps that can be reversed iteratively. Three contributions are made: (i) a diffusion process suitable for the decoding setting is introduced, (ii) the neural diffusion decoder is conditioned on the number of parity errors, which indicates the level of corruption at a given step, (iii) a line search procedure based on the code's syndrome obtains the optimal reverse diffusion step size. The proposed approach demonstrates the power of diffusion models for ECC and is able to achieve state of the art accuracy, outperforming the other neural decoders by sizable margins, even for a single reverse diffusion step.

Error Correction Code Transformer

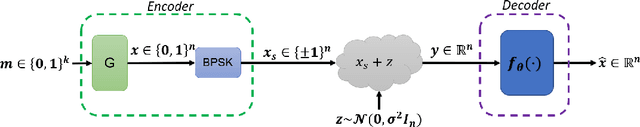
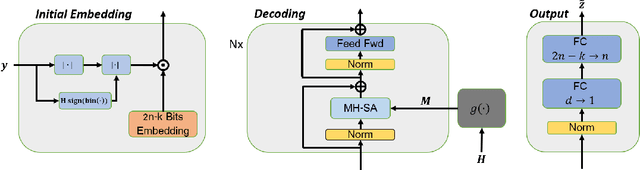
Error correction code is a major part of the communication physical layer, ensuring the reliable transfer of data over noisy channels. Recently, neural decoders were shown to outperform classical decoding techniques. However, the existing neural approaches present strong overfitting due to the exponential training complexity, or a restrictive inductive bias due to reliance on Belief Propagation. Recently, Transformers have become methods of choice in many applications thanks to their ability to represent complex interactions between elements. In this work, we propose to extend for the first time the Transformer architecture to the soft decoding of linear codes at arbitrary block lengths. We encode each channel's output dimension to high dimension for better representation of the bits information to be processed separately. The element-wise processing allows the analysis of the channel output reliability, while the algebraic code and the interaction between the bits are inserted into the model via an adapted masked self-attention module. The proposed approach demonstrates the extreme power and flexibility of Transformers and outperforms existing state-of-the-art neural decoders by large margins at a fraction of their time complexity.

Meta Subspace Optimization

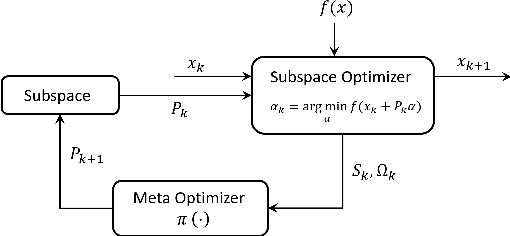
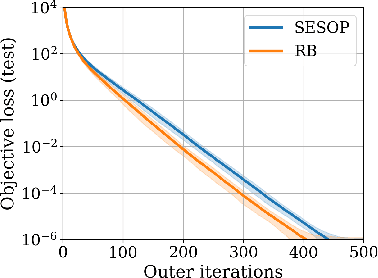
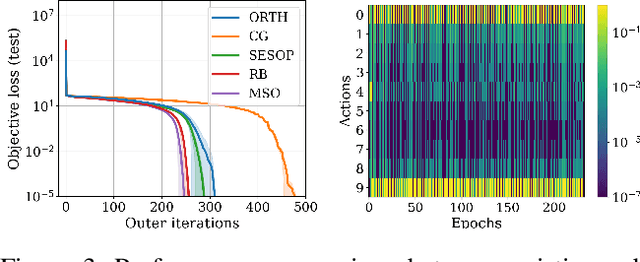
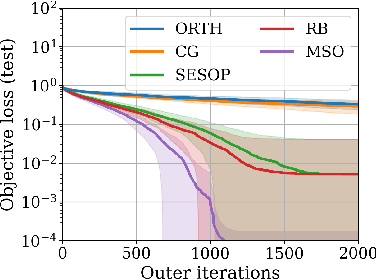
Subspace optimization methods have the attractive property of reducing large-scale optimization problems to a sequence of low-dimensional subspace optimization problems. However, existing subspace optimization frameworks adopt a fixed update policy of the subspace, and therefore, appear to be sub-optimal. In this paper we propose a new \emph{Meta Subspace Optimization} (MSO) framework for large-scale optimization problems, which allows to determine the subspace matrix at each optimization iteration. In order to remain invariant to the optimization problem's dimension, we design an efficient meta optimizer based on very low-dimensional subspace optimization coefficients, inducing a rule-based agent that can significantly improve performance. Finally, we design and analyze a reinforcement learning procedure based on the subspace optimization dynamics whose learnt policies outperform existing subspace optimization methods.

Geometric Transformer for End-to-End Molecule Properties Prediction

Transformers have become methods of choice in many applications thanks to their ability to represent complex interaction between elements. However, extending the Transformer architecture to non-sequential data such as molecules and enabling its training on small datasets remain a challenge. In this work, we introduce a Transformer-based architecture for molecule property prediction, which is able to capture the geometry of the molecule. We modify the classical positional encoder by an initial encoding of the molecule geometry, as well as a learned gated self-attention mechanism. We further suggest an augmentation scheme for molecular data capable of avoiding the overfitting induced by the overparameterized architecture. The proposed framework outperforms the state-of-the-art methods while being based on pure machine learning solely, i.e. the method does not incorporate domain knowledge from quantum chemistry and does not use extended geometric inputs beside the pairwise atomic distances.