Adaptive Consensus Gradients Aggregation for Scaled Distributed Training

Distributed machine learning has recently become a critical paradigm for training large models on vast datasets. We examine the stochastic optimization problem for deep learning within synchronous parallel computing environments under communication constraints. While averaging distributed gradients is the most widely used method for gradient estimation, whether this is the optimal strategy remains an open question. In this work, we analyze the distributed gradient aggregation process through the lens of subspace optimization. By formulating the aggregation problem as an objective-aware subspace optimization problem, we derive an efficient weighting scheme for gradients, guided by subspace coefficients. We further introduce subspace momentum to accelerate convergence while maintaining statistical unbiasedness in the aggregation. Our method demonstrates improved performance over the ubiquitous gradient averaging on multiple MLPerf tasks while remaining extremely efficient in both communicational and computational complexity.

Primal-Dual Sequential Subspace Optimization for Saddle-point Problems

We introduce a new sequential subspace optimization method for large-scale saddle-point problems. It solves iteratively a sequence of auxiliary saddle-point problems in low-dimensional subspaces, spanned by directions derived from first-order information over the primal \emph{and} dual variables. Proximal regularization is further deployed to stabilize the optimization process. Experimental results demonstrate significantly better convergence relative to popular first-order methods. We analyze the influence of the subspace on the convergence of the algorithm, and assess its performance in various deterministic optimization scenarios, such as bi-linear games, ADMM-based constrained optimization and generative adversarial networks.

Low-bit Quantization of Neural Networks for Efficient Inference

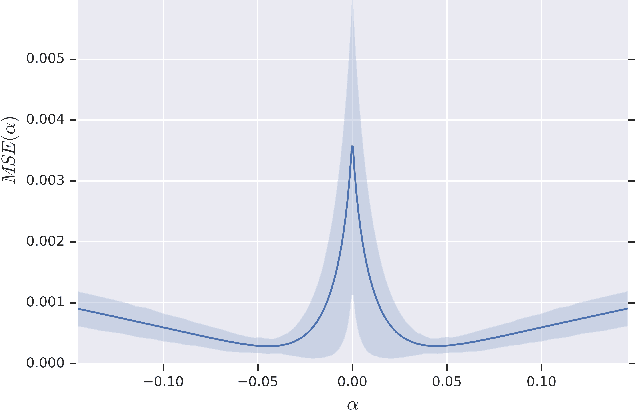
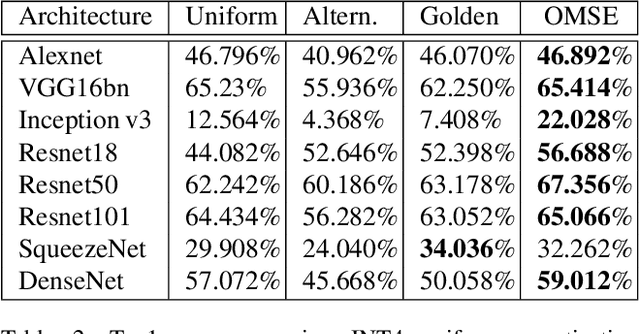
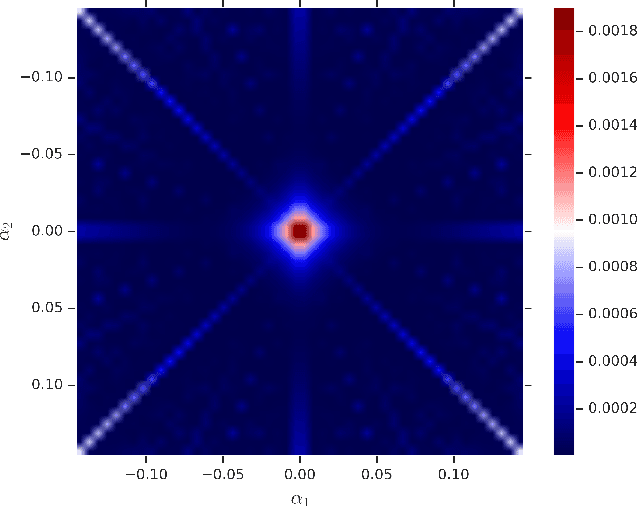
Recent machine learning methods use increasingly large deep neural networks to achieve state of the art results in various tasks. The gains in performance come at the cost of a substantial increase in computation and storage requirements. This makes real-time implementations on limited resources hardware a challenging task. One popular approach to address this challenge is to perform low-bit precision computations via neural network quantization. However, aggressive quantization generally entails a severe penalty in terms of accuracy, and often requires retraining of the network, or resorting to higher bit precision quantization. In this paper, we formalize the linear quantization task as a Minimum Mean Squared Error (MMSE) problem for both weights and activations, allowing low-bit precision inference without the need for full network retraining. The main contributions of our approach are the optimizations of the constrained MSE problem at each layer of the network, the hardware aware partitioning of the network parameters, and the use of multiple low precision quantized tensors for poorly approximated layers. The proposed approach allows 4 bits integer (INT4) quantization for deployment of pretrained models on limited hardware resources. Multiple experiments on various network architectures show that the suggested method yields state of the art results with minimal loss of tasks accuracy.

Deep Learning for Decoding of Linear Codes - A Syndrome-Based Approach

We present a novel framework for applying deep neural networks (DNN) to soft decoding of linear codes at arbitrary block lengths. Unlike other approaches, our framework allows unconstrained DNN design, enabling the free application of powerful designs that were developed in other contexts. Our method is robust to overfitting that inhibits many competing methods, which follows from the exponentially large number of codewords required for their training. We achieve this by transforming the channel output before feeding it to the network, extracting only the syndrome of the hard decisions and the channel output reliabilities. We prove analytically that this approach does not involve any intrinsic performance penalty, and guarantees the generalization of performance obtained during training. Our best results are obtained using a recurrent neural network (RNN) architecture combined with simple preprocessing by permutation. We provide simulation results that demonstrate performance that sometimes approaches that of the ordered statistics decoding (OSD) algorithm.