Low-bit Quantization of Neural Networks for Efficient Inference
Paper and Code
Mar 25, 2019
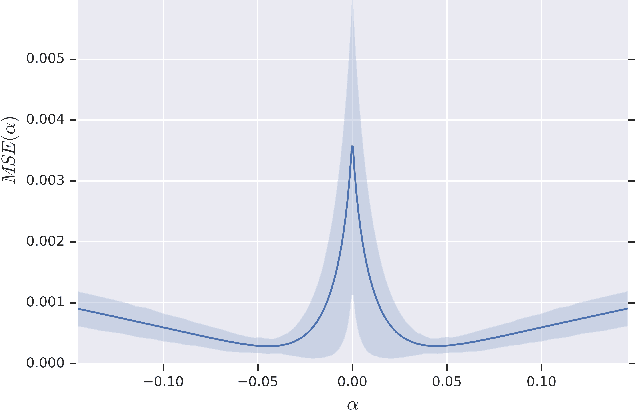
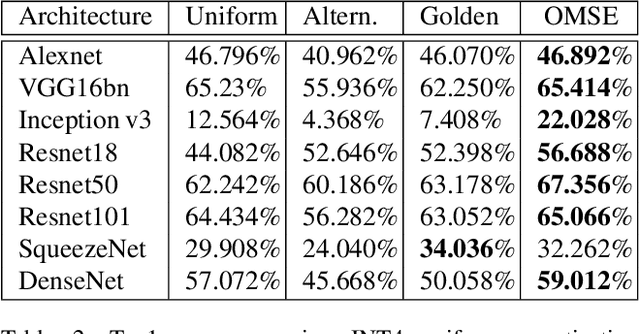
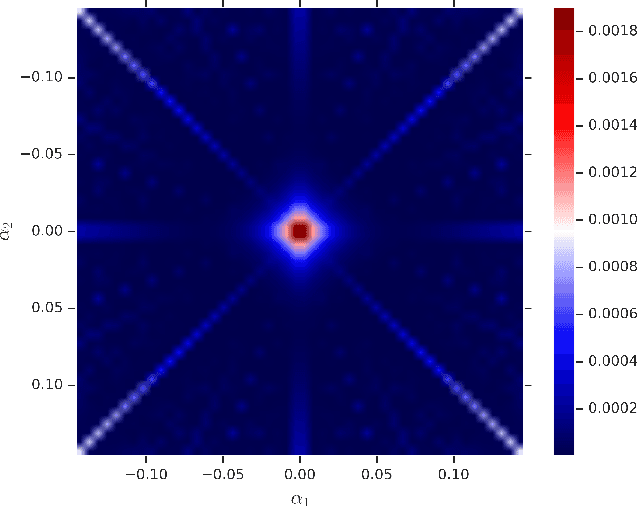
Recent machine learning methods use increasingly large deep neural networks to achieve state of the art results in various tasks. The gains in performance come at the cost of a substantial increase in computation and storage requirements. This makes real-time implementations on limited resources hardware a challenging task. One popular approach to address this challenge is to perform low-bit precision computations via neural network quantization. However, aggressive quantization generally entails a severe penalty in terms of accuracy, and often requires retraining of the network, or resorting to higher bit precision quantization. In this paper, we formalize the linear quantization task as a Minimum Mean Squared Error (MMSE) problem for both weights and activations, allowing low-bit precision inference without the need for full network retraining. The main contributions of our approach are the optimizations of the constrained MSE problem at each layer of the network, the hardware aware partitioning of the network parameters, and the use of multiple low precision quantized tensors for poorly approximated layers. The proposed approach allows 4 bits integer (INT4) quantization for deployment of pretrained models on limited hardware resources. Multiple experiments on various network architectures show that the suggested method yields state of the art results with minimal loss of tasks accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge