Learning Invariant Representations Of Planar Curves
Paper and Code
Feb 16, 2017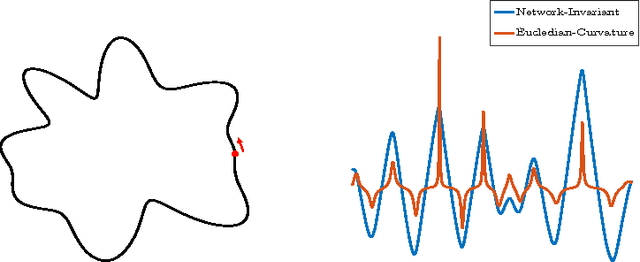
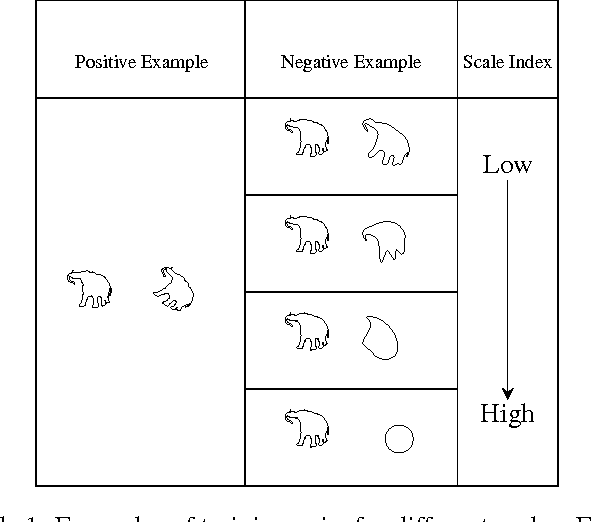
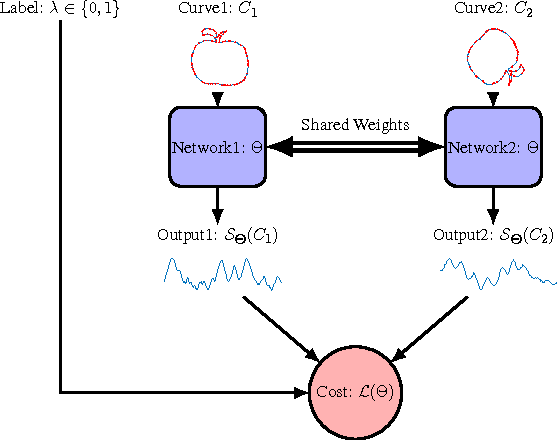
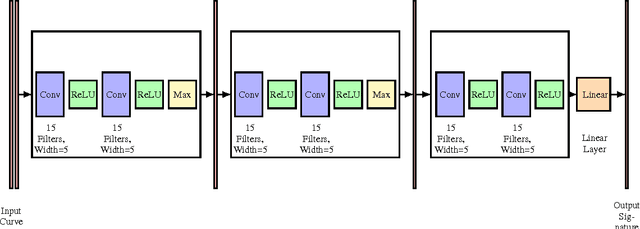
We propose a metric learning framework for the construction of invariant geometric functions of planar curves for the Eucledian and Similarity group of transformations. We leverage on the representational power of convolutional neural networks to compute these geometric quantities. In comparison with axiomatic constructions, we show that the invariants approximated by the learning architectures have better numerical qualities such as robustness to noise, resiliency to sampling, as well as the ability to adapt to occlusion and partiality. Finally, we develop a novel multi-scale representation in a similarity metric learning paradigm.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge