StarNet: towards weakly supervised few-shot detection and explainable few-shot classification

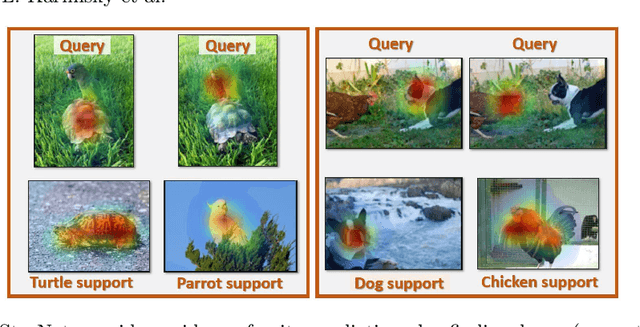
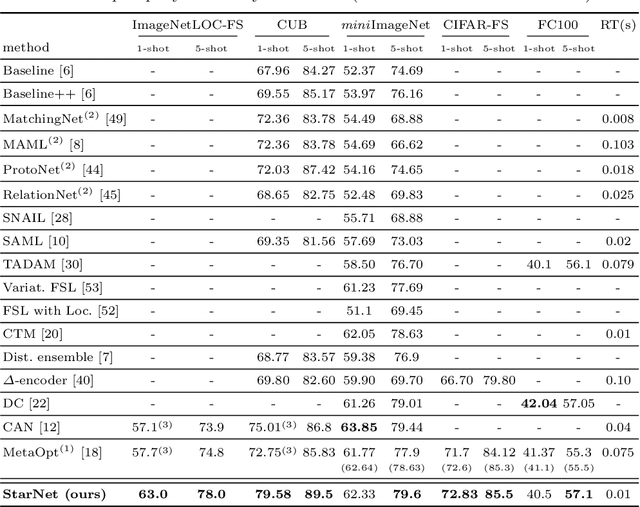
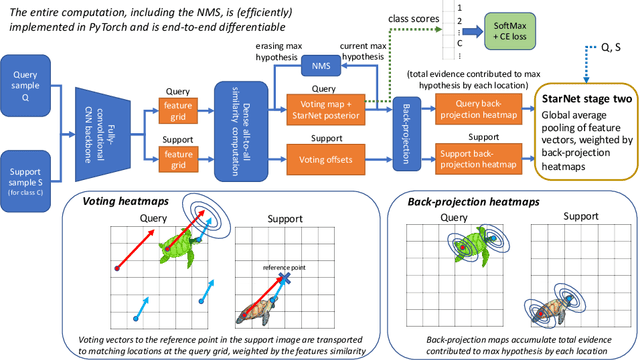
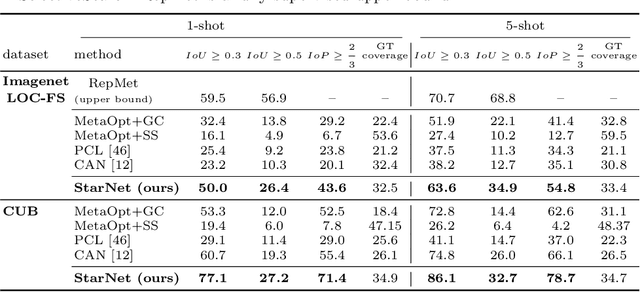
In this paper, we propose a new few-shot learning method called StarNet, which is an end-to-end trainable non-parametric star-model few-shot classifier. While being meta-trained using only image-level class labels, StarNet learns not only to predict the class labels for each query image of a few-shot task, but also to localize (via a heatmap) what it believes to be the key image regions supporting its prediction, thus effectively detecting the instances of the novel categories. The localization is enabled by the StarNet's ability to find large, arbitrarily shaped, semantically matching regions between all pairs of support and query images of a few-shot task. We evaluate StarNet on multiple few-shot classification benchmarks attaining significant state-of-the-art improvement on the CUB and ImageNetLOC-FS, and smaller improvements on other benchmarks. At the same time, in many cases, StarNet provides plausible explanations for its class label predictions, by highlighting the correctly paired novel category instances on the query and on its best matching support (for the predicted class). In addition, we test the proposed approach on the previously unexplored and challenging task of Weakly Supervised Few-Shot Object Detection (WS-FSOD), obtaining significant improvements over the baselines.

TAFSSL: Task-Adaptive Feature Sub-Space Learning for few-shot classification

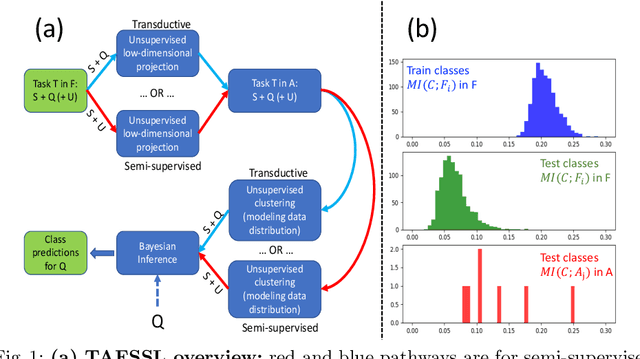
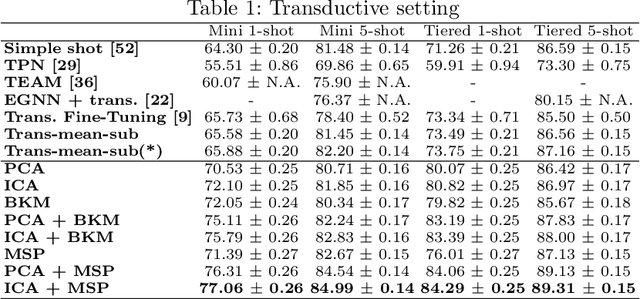
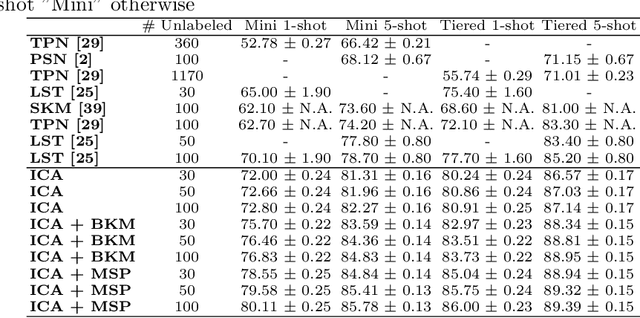
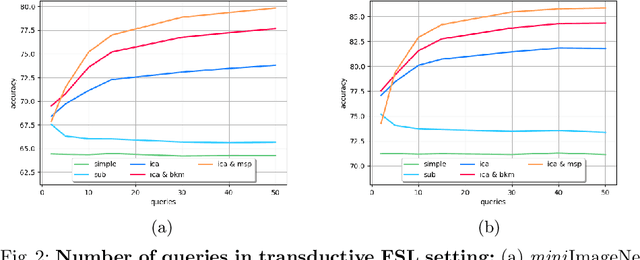
The field of Few-Shot Learning (FSL), or learning from very few (typically $1$ or $5$) examples per novel class (unseen during training), has received a lot of attention and significant performance advances in the recent literature. While number of techniques have been proposed for FSL, several factors have emerged as most important for FSL performance, awarding SOTA even to the simplest of techniques. These are: the backbone architecture (bigger is better), type of pre-training on the base classes (meta-training vs regular multi-class, currently regular wins), quantity and diversity of the base classes set (the more the merrier, resulting in richer and better adaptive features), and the use of self-supervised tasks during pre-training (serving as a proxy for increasing the diversity of the base set). In this paper we propose yet another simple technique that is important for the few shot learning performance - a search for a compact feature sub-space that is discriminative for a given few-shot test task. We show that the Task-Adaptive Feature Sub-Space Learning (TAFSSL) can significantly boost the performance in FSL scenarios when some additional unlabeled data accompanies the novel few-shot task, be it either the set of unlabeled queries (transductive FSL) or some additional set of unlabeled data samples (semi-supervised FSL). Specifically, we show that on the challenging miniImageNet and tieredImageNet benchmarks, TAFSSL can improve the current state-of-the-art in both transductive and semi-supervised FSL settings by more than $5\%$, while increasing the benefit of using unlabeled data in FSL to above $10\%$ performance gain.

Deep Eikonal Solvers

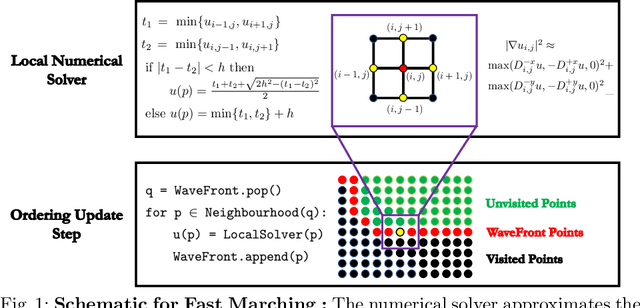
A deep learning approach to numerically approximate the solution to the Eikonal equation is introduced. The proposed method is built on the fast marching scheme which comprises of two components: a local numerical solver and an update scheme. We replace the formulaic local numerical solver with a trained neural network to provide highly accurate estimates of local distances for a variety of different geometries and sampling conditions. Our learning approach generalizes not only to flat Euclidean domains but also to curved surfaces enabled by the incorporation of certain invariant features in the neural network architecture. We show a considerable gain in performance, validated by smaller errors and higher orders of accuracy for the numerical solutions of the Eikonal equation computed on different surfaces The proposed approach leverages the approximation power of neural networks to enhance the performance of numerical algorithms, thereby, connecting the somewhat disparate themes of numerical geometry and learning.