Why you should learn functional basis
Paper and Code
Dec 14, 2021
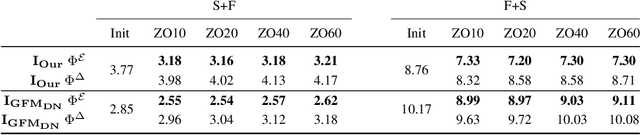
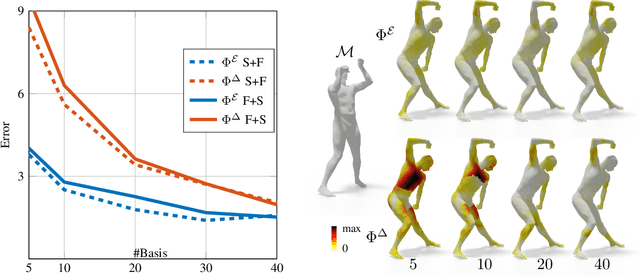
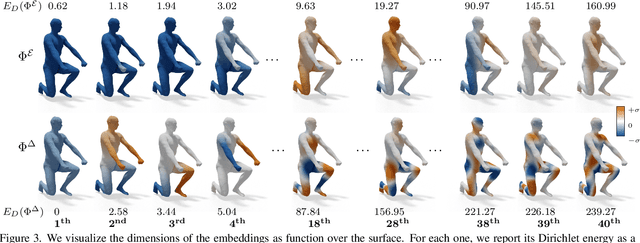
Efficient and practical representation of geometric data is a ubiquitous problem for several applications in geometry processing. A widely used choice is to encode the 3D objects through their spectral embedding, associating to each surface point the values assumed at that point by a truncated subset of the eigenfunctions of a differential operator (typically the Laplacian). Several attempts to define new, preferable embeddings for different applications have seen the light during the last decade. Still, the standard Laplacian eigenfunctions remain solidly at the top of the available solutions, despite their limitations, such as being limited to near-isometries for shape matching. Recently, a new trend shows advantages in learning substitutes for the Laplacian eigenfunctions. At the same time, many research questions remain unsolved: are the new bases better than the LBO eigenfunctions, and how do they relate to them? How do they act in the functional perspective? And how to exploit these bases in new configurations in conjunction with additional features and descriptors? In this study, we properly pose these questions to improve our understanding of this emerging research direction. We show their applicative relevance in different contexts revealing some of their insights and exciting future directions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge