Denoising Functional Maps: Diffusion Models for Shape Correspondence

Estimating correspondences between pairs of deformable shapes remains a challenging problem. Despite substantial progress, existing methods lack broad generalization capabilities and require category-specific training data. To address these limitations, we propose a fundamentally new approach to shape correspondence based on denoising diffusion models. In our method, a diffusion model learns to directly predict the functional map, a low-dimensional representation of a point-wise map between shapes. We use a large dataset of synthetic human meshes for training and employ two steps to reduce the number of functional maps that need to be learned. First, the maps refer to a template rather than shape pairs. Second, the functional map is defined in a basis of eigenvectors of the Laplacian, which is not unique due to sign ambiguity. Therefore, we introduce an unsupervised approach to select a specific basis by correcting the signs of eigenvectors based on surface features. Our approach achieves competitive performance on standard human datasets, meshes with anisotropic connectivity, non-isometric humanoid shapes, as well as animals compared to existing descriptor-based and large-scale shape deformation methods.

Laplace-Beltrami Operator for Gaussian Splatting

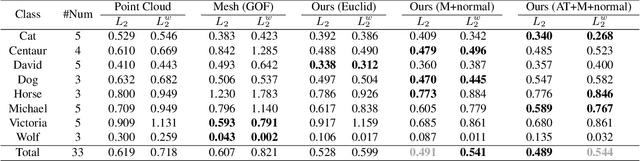
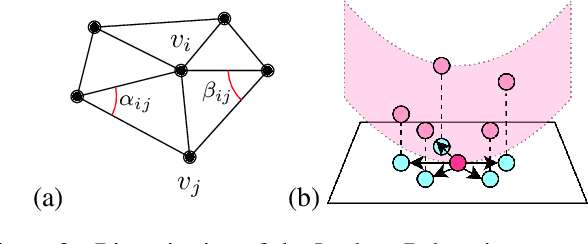
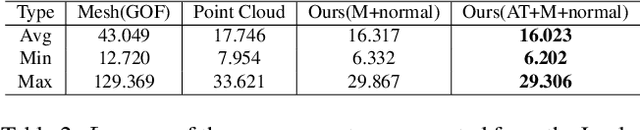
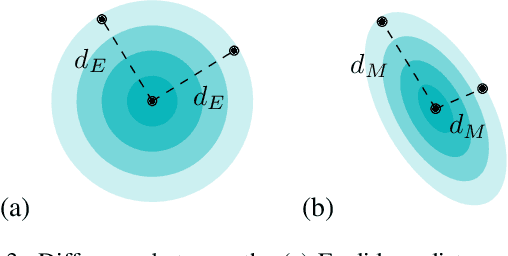
With the rising popularity of 3D Gaussian splatting and the expanse of applications from rendering to 3D reconstruction, there comes also a need for geometry processing applications directly on this new representation. While considering the centers of Gaussians as a point cloud or meshing them is an option that allows to apply existing algorithms, this might ignore information present in the data or be unnecessarily expensive. Additionally, Gaussian splatting tends to contain a large number of outliers which do not affect the rendering quality but need to be handled correctly in order not to produce noisy results in geometry processing applications. In this work, we propose a formulation to compute the Laplace-Beltrami operator, a widely used tool in geometry processing, directly on Gaussian splatting using the Mahalanobis distance. While conceptually similar to a point cloud Laplacian, our experiments show superior accuracy on the point clouds encoded in the Gaussian splatting centers and, additionally, the operator can be used to evaluate the quality of the output during optimization.

Beyond Complete Shapes: A quantitative Evaluation of 3D Shape Matching Algorithms

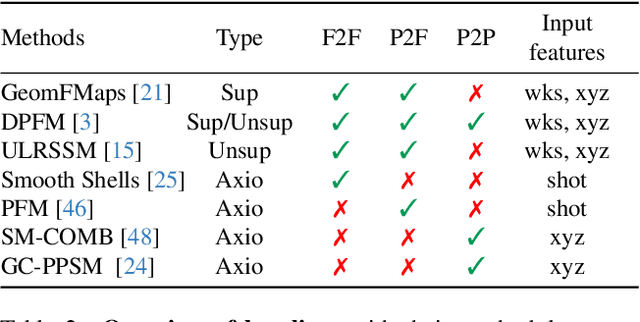
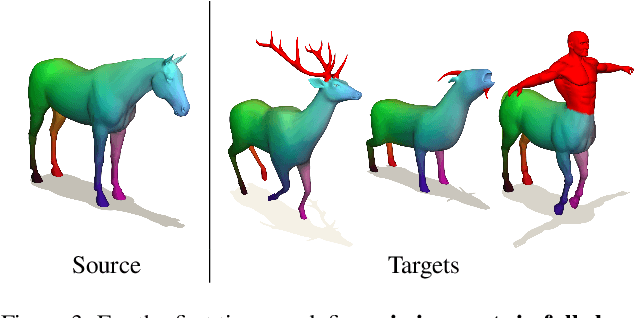
Finding correspondences between 3D shapes is an important and long-standing problem in computer vision, graphics and beyond. While approaches based on machine learning dominate modern 3D shape matching, almost all existing (learning-based) methods require that at least one of the involved shapes is complete. In contrast, the most challenging and arguably most practically relevant setting of matching partially observed shapes, is currently underexplored. One important factor is that existing datasets contain only a small number of shapes (typically below 100), which are unable to serve data-hungry machine learning approaches, particularly in the unsupervised regime. In addition, the type of partiality present in existing datasets is often artificial and far from realistic. To address these limitations and to encourage research on these relevant settings, we provide a generic and flexible framework for the procedural generation of challenging partial shape matching scenarios. Our framework allows for a virtually infinite generation of partial shape matching instances from a finite set of shapes with complete geometry. Further, we manually create cross-dataset correspondences between seven existing (complete geometry) shape matching datasets, leading to a total of 2543 shapes. Based on this, we propose several challenging partial benchmark settings, for which we evaluate respective state-of-the-art methods as baselines.

3D Shape Completion with Test-Time Training

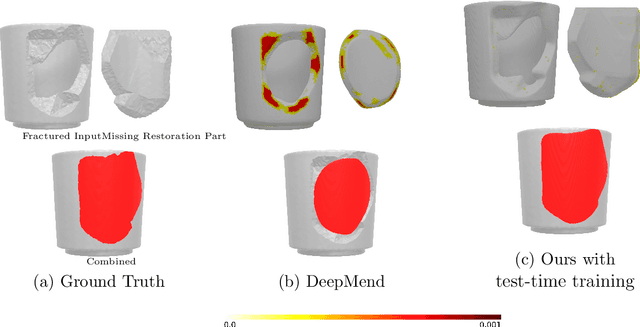
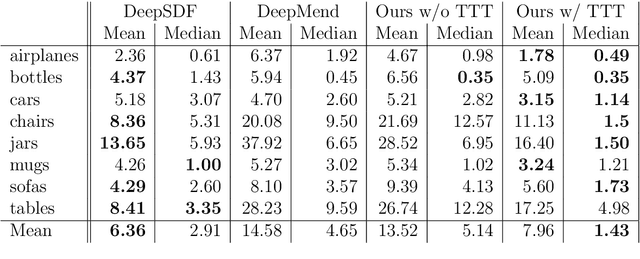
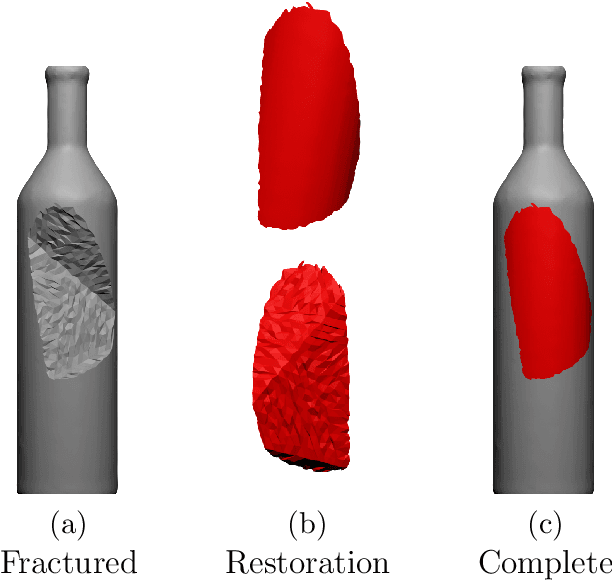
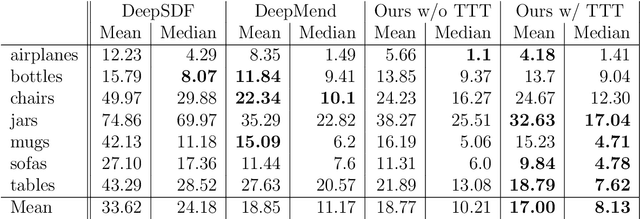
This work addresses the problem of \textit{shape completion}, i.e., the task of restoring incomplete shapes by predicting their missing parts. While previous works have often predicted the fractured and restored shape in one step, we approach the task by separately predicting the fractured and newly restored parts, but ensuring these predictions are interconnected. We use a decoder network motivated by related work on the prediction of signed distance functions (DeepSDF). In particular, our representation allows us to consider test-time-training, i.e., finetuning network parameters to match the given incomplete shape more accurately during inference. While previous works often have difficulties with artifacts around the fracture boundary, we demonstrate that our overfitting to the fractured parts leads to significant improvements in the restoration of eight different shape categories of the ShapeNet data set in terms of their chamfer distances.

Implicit-ARAP: Efficient Handle-Guided Deformation of High-Resolution Meshes and Neural Fields via Local Patch Meshing

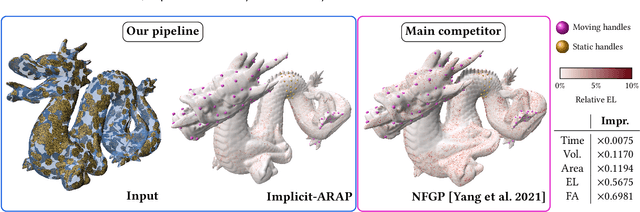
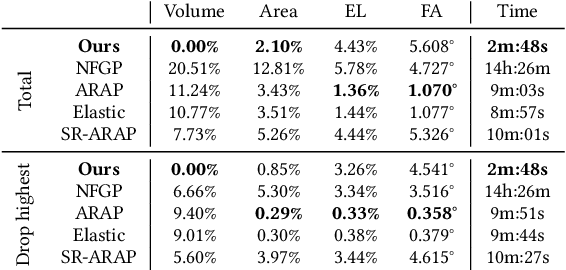
In this work, we present the local patch mesh representation for neural signed distance fields. This technique allows to discretize local regions of the level sets of an input SDF by projecting and deforming flat patch meshes onto the level set surface, using exclusively the SDF information and its gradient. Our analysis reveals this method to be more accurate than the standard marching cubes algorithm for approximating the implicit surface. Then, we apply this representation in the setting of handle-guided deformation: we introduce two distinct pipelines, which make use of 3D neural fields to compute As-Rigid-As-Possible deformations of both high-resolution meshes and neural fields under a given set of constraints. We run a comprehensive evaluation of our method and various baselines for neural field and mesh deformation which show both pipelines achieve impressive efficiency and notable improvements in terms of quality of results and robustness. With our novel pipeline, we introduce a scalable approach to solve a well-established geometry processing problem on high-resolution meshes, and pave the way for extending other geometric tasks to the domain of implicit surfaces via local patch meshing.

Hybrid Functional Maps for Crease-Aware Non-Isometric Shape Matching

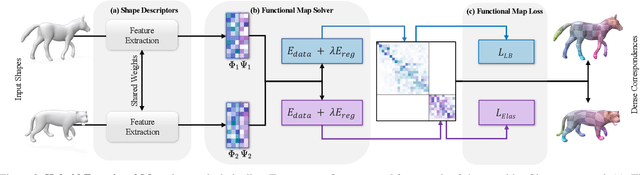
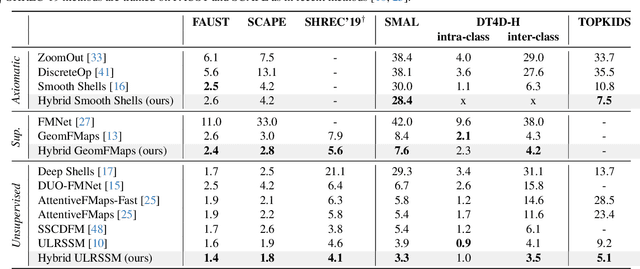
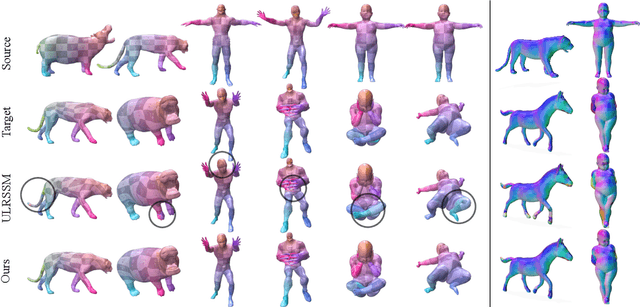
Non-isometric shape correspondence remains a fundamental challenge in computer vision. Traditional methods using Laplace-Beltrami operator (LBO) eigenmodes face limitations in characterizing high-frequency extrinsic shape changes like bending and creases. We propose a novel approach of combining the non-orthogonal extrinsic basis of eigenfunctions of the elastic thin-shell hessian with the intrinsic ones of the LBO, creating a hybrid spectral space in which we construct functional maps. To this end, we present a theoretical framework to effectively integrate non-orthogonal basis functions into descriptor- and learning-based functional map methods. Our approach can be incorporated easily into existing functional map pipelines across varying applications and is able to handle complex deformations beyond isometries. We show extensive evaluations across various supervised and unsupervised settings and demonstrate significant improvements. Notably, our approach achieves up to 15% better mean geodesic error for non-isometric correspondence settings and up to 45% improvement in scenarios with topological noise.

Kissing to Find a Match: Efficient Low-Rank Permutation Representation

Permutation matrices play a key role in matching and assignment problems across the fields, especially in computer vision and robotics. However, memory for explicitly representing permutation matrices grows quadratically with the size of the problem, prohibiting large problem instances. In this work, we propose to tackle the curse of dimensionality of large permutation matrices by approximating them using low-rank matrix factorization, followed by a nonlinearity. To this end, we rely on the Kissing number theory to infer the minimal rank required for representing a permutation matrix of a given size, which is significantly smaller than the problem size. This leads to a drastic reduction in computation and memory costs, e.g., up to $3$ orders of magnitude less memory for a problem of size $n=20000$, represented using $8.4\times10^5$ elements in two small matrices instead of using a single huge matrix with $4\times 10^8$ elements. The proposed representation allows for accurate representations of large permutation matrices, which in turn enables handling large problems that would have been infeasible otherwise. We demonstrate the applicability and merits of the proposed approach through a series of experiments on a range of problems that involve predicting permutation matrices, from linear and quadratic assignment to shape matching problems.

SIGMA: Scale-Invariant Global Sparse Shape Matching

We propose a novel mixed-integer programming (MIP) formulation for generating precise sparse correspondences for highly non-rigid shapes. To this end, we introduce a projected Laplace-Beltrami operator (PLBO) which combines intrinsic and extrinsic geometric information to measure the deformation quality induced by predicted correspondences. We integrate the PLBO, together with an orientation-aware regulariser, into a novel MIP formulation that can be solved to global optimality for many practical problems. In contrast to previous methods, our approach is provably invariant to rigid transformations and global scaling, initialisation-free, has optimality guarantees, and scales to high resolution meshes with (empirically observed) linear time. We show state-of-the-art results for sparse non-rigid matching on several challenging 3D datasets, including data with inconsistent meshing, as well as applications in mesh-to-point-cloud matching.

CCuantuMM: Cycle-Consistent Quantum-Hybrid Matching of Multiple Shapes

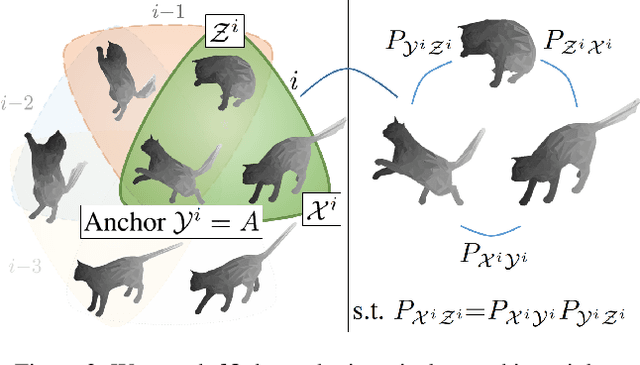
Jointly matching multiple, non-rigidly deformed 3D shapes is a challenging, $\mathcal{NP}$-hard problem. A perfect matching is necessarily cycle-consistent: Following the pairwise point correspondences along several shapes must end up at the starting vertex of the original shape. Unfortunately, existing quantum shape-matching methods do not support multiple shapes and even less cycle consistency. This paper addresses the open challenges and introduces the first quantum-hybrid approach for 3D shape multi-matching; in addition, it is also cycle-consistent. Its iterative formulation is admissible to modern adiabatic quantum hardware and scales linearly with the total number of input shapes. Both these characteristics are achieved by reducing the $N$-shape case to a sequence of three-shape matchings, the derivation of which is our main technical contribution. Thanks to quantum annealing, high-quality solutions with low energy are retrieved for the intermediate $\mathcal{NP}$-hard objectives. On benchmark datasets, the proposed approach significantly outperforms extensions to multi-shape matching of a previous quantum-hybrid two-shape matching method and is on-par with classical multi-matching methods.

Conjugate Product Graphs for Globally Optimal 2D-3D Shape Matching

We consider the problem of finding a continuous and non-rigid matching between a 2D contour and a 3D mesh. While such problems can be solved to global optimality by finding a shortest path in the product graph between both shapes, existing solutions heavily rely on unrealistic prior assumptions to avoid degenerate solutions (e.g. knowledge to which region of the 3D shape each point of the 2D contour is matched). To address this, we propose a novel 2D-3D shape matching formalism based on the conjugate product graph between the 2D contour and the 3D shape. Doing so allows us for the first time to consider higher-order costs, i.e. defined for edge chains, as opposed to costs defined for single edges. This offers substantially more flexibility, which we utilise to incorporate a local rigidity prior. By doing so, we effectively circumvent degenerate solutions and thereby obtain smoother and more realistic matchings, even when using only a one-dimensional feature descriptor. Overall, our method finds globally optimal and continuous 2D-3D matchings, has the same asymptotic complexity as previous solutions, produces state-of-the-art results for shape matching and is even capable of matching partial shapes.