Symmetry Informative and Agnostic Feature Disentanglement for 3D Shapes

Shape descriptors, i.e., per-vertex features of 3D meshes or point clouds, are fundamental to shape analysis. Historically, various handcrafted geometry-aware descriptors and feature refinement techniques have been proposed. Recently, several studies have initiated a new research direction by leveraging features from image foundation models to create semantics-aware descriptors, demonstrating advantages across tasks like shape matching, editing, and segmentation. Symmetry, another key concept in shape analysis, has also attracted increasing attention. Consequently, constructing symmetry-aware shape descriptors is a natural progression. Although the recent method $χ$ (Wang et al., 2025) successfully extracted symmetry-informative features from semantic-aware descriptors, its features are only one-dimensional, neglecting other valuable semantic information. Furthermore, the extracted symmetry-informative feature is usually noisy and yields small misclassified patches. To address these gaps, we propose a feature disentanglement approach which is simultaneously symmetry informative and symmetry agnostic. Further, we propose a feature refinement technique to improve the robustness of predicted symmetry informative features. Extensive experiments, including intrinsic symmetry detection, left/right classification, and shape matching, demonstrate the effectiveness of our proposed framework compared to various state-of-the-art methods, both qualitatively and quantitatively.

Symmetry Understanding of 3D Shapes via Chirality Disentanglement

Chirality information (i.e. information that allows distinguishing left from right) is ubiquitous for various data modes in computer vision, including images, videos, point clouds, and meshes. While chirality has been extensively studied in the image domain, its exploration in shape analysis (such as point clouds and meshes) remains underdeveloped. Although many shape vertex descriptors have shown appealing properties (e.g. robustness to rigid-body transformations), they are often not able to disambiguate between left and right symmetric parts. Considering the ubiquity of chirality information in different shape analysis problems and the lack of chirality-aware features within current shape descriptors, developing a chirality feature extractor becomes necessary and urgent. Based on the recent Diff3F framework, we propose an unsupervised chirality feature extraction pipeline to decorate shape vertices with chirality-aware information, extracted from 2D foundation models. We evaluated the extracted chirality features through quantitative and qualitative experiments across diverse datasets. Results from downstream tasks including left-right disentanglement, shape matching, and part segmentation demonstrate their effectiveness and practical utility. Project page: https://wei-kang-wang.github.io/chirality/

Beyond Complete Shapes: A quantitative Evaluation of 3D Shape Matching Algorithms

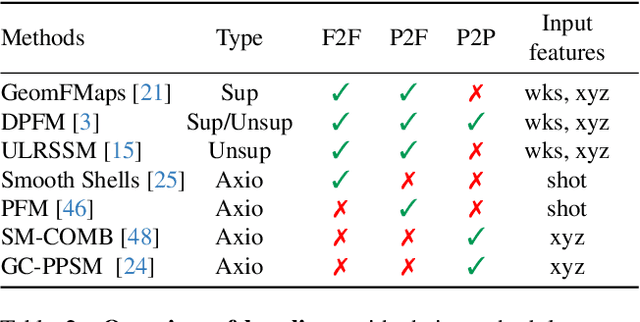
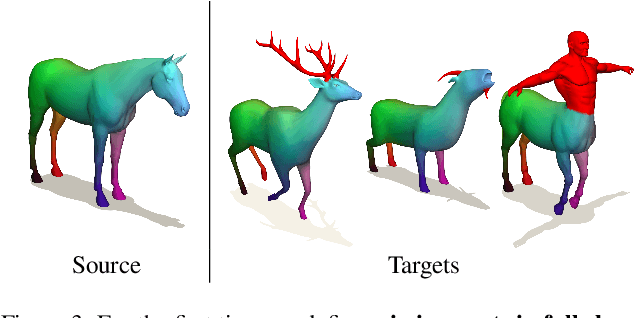
Finding correspondences between 3D shapes is an important and long-standing problem in computer vision, graphics and beyond. While approaches based on machine learning dominate modern 3D shape matching, almost all existing (learning-based) methods require that at least one of the involved shapes is complete. In contrast, the most challenging and arguably most practically relevant setting of matching partially observed shapes, is currently underexplored. One important factor is that existing datasets contain only a small number of shapes (typically below 100), which are unable to serve data-hungry machine learning approaches, particularly in the unsupervised regime. In addition, the type of partiality present in existing datasets is often artificial and far from realistic. To address these limitations and to encourage research on these relevant settings, we provide a generic and flexible framework for the procedural generation of challenging partial shape matching scenarios. Our framework allows for a virtually infinite generation of partial shape matching instances from a finite set of shapes with complete geometry. Further, we manually create cross-dataset correspondences between seven existing (complete geometry) shape matching datasets, leading to a total of 2543 shapes. Based on this, we propose several challenging partial benchmark settings, for which we evaluate respective state-of-the-art methods as baselines.

Spectral Meets Spatial: Harmonising 3D Shape Matching and Interpolation

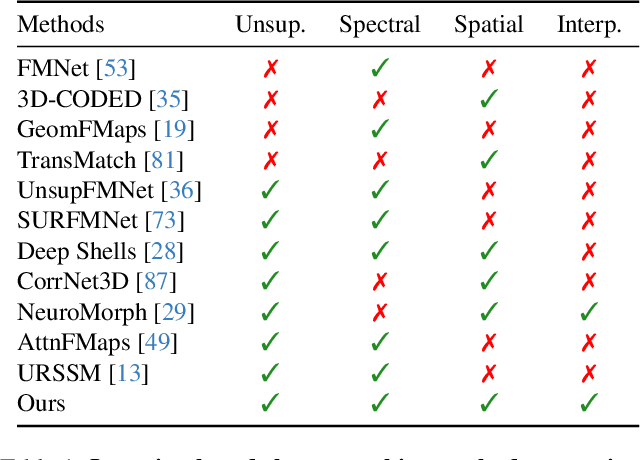
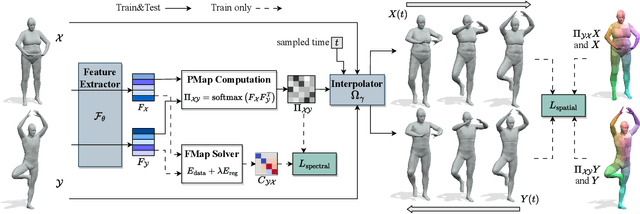
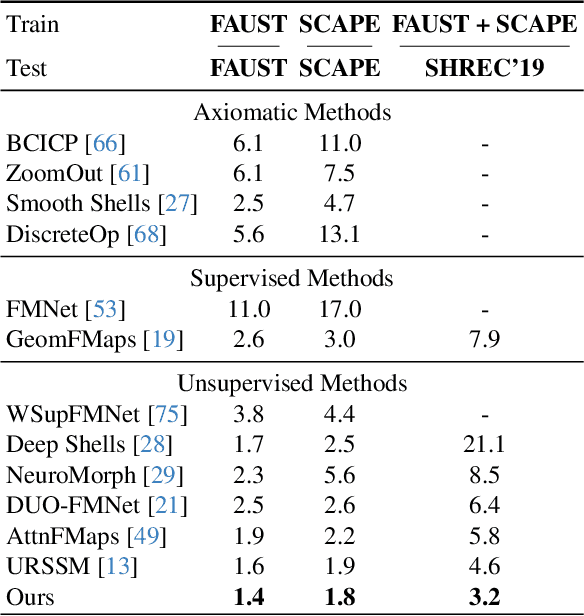
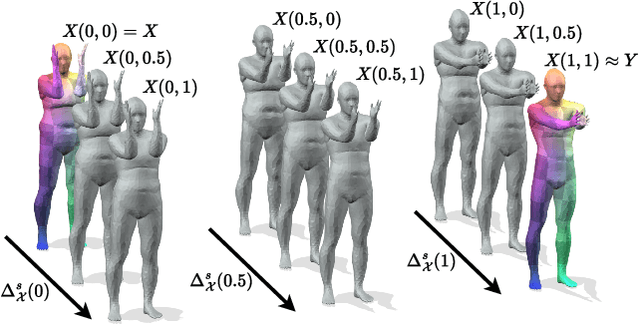
Although 3D shape matching and interpolation are highly interrelated, they are often studied separately and applied sequentially to relate different 3D shapes, thus resulting in sub-optimal performance. In this work we present a unified framework to predict both point-wise correspondences and shape interpolation between 3D shapes. To this end, we combine the deep functional map framework with classical surface deformation models to map shapes in both spectral and spatial domains. On the one hand, by incorporating spatial maps, our method obtains more accurate and smooth point-wise correspondences compared to previous functional map methods for shape matching. On the other hand, by introducing spectral maps, our method gets rid of commonly used but computationally expensive geodesic distance constraints that are only valid for near-isometric shape deformations. Furthermore, we propose a novel test-time adaptation scheme to capture both pose-dominant and shape-dominant deformations. Using different challenging datasets, we demonstrate that our method outperforms previous state-of-the-art methods for both shape matching and interpolation, even compared to supervised approaches.