TwoSquared: 4D Generation from 2D Image Pairs

Despite the astonishing progress in generative AI, 4D dynamic object generation remains an open challenge. With limited high-quality training data and heavy computing requirements, the combination of hallucinating unseen geometry together with unseen movement poses great challenges to generative models. In this work, we propose TwoSquared as a method to obtain a 4D physically plausible sequence starting from only two 2D RGB images corresponding to the beginning and end of the action. Instead of directly solving the 4D generation problem, TwoSquared decomposes the problem into two steps: 1) an image-to-3D module generation based on the existing generative model trained on high-quality 3D assets, and 2) a physically inspired deformation module to predict intermediate movements. To this end, our method does not require templates or object-class-specific prior knowledge and can take in-the-wild images as input. In our experiments, we demonstrate that TwoSquared is capable of producing texture-consistent and geometry-consistent 4D sequences only given 2D images.

PRISM: Probabilistic Representation for Integrated Shape Modeling and Generation

Despite the advancements in 3D full-shape generation, accurately modeling complex geometries and semantics of shape parts remains a significant challenge, particularly for shapes with varying numbers of parts. Current methods struggle to effectively integrate the contextual and structural information of 3D shapes into their generative processes. We address these limitations with PRISM, a novel compositional approach for 3D shape generation that integrates categorical diffusion models with Statistical Shape Models (SSM) and Gaussian Mixture Models (GMM). Our method employs compositional SSMs to capture part-level geometric variations and uses GMM to represent part semantics in a continuous space. This integration enables both high fidelity and diversity in generated shapes while preserving structural coherence. Through extensive experiments on shape generation and manipulation tasks, we demonstrate that our approach significantly outperforms previous methods in both quality and controllability of part-level operations. Our code will be made publicly available.

4Deform: Neural Surface Deformation for Robust Shape Interpolation

Generating realistic intermediate shapes between non-rigidly deformed shapes is a challenging task in computer vision, especially with unstructured data (e.g., point clouds) where temporal consistency across frames is lacking, and topologies are changing. Most interpolation methods are designed for structured data (i.e., meshes) and do not apply to real-world point clouds. In contrast, our approach, 4Deform, leverages neural implicit representation (NIR) to enable free topology changing shape deformation. Unlike previous mesh-based methods that learn vertex-based deformation fields, our method learns a continuous velocity field in Euclidean space. Thus, it is suitable for less structured data such as point clouds. Additionally, our method does not require intermediate-shape supervision during training; instead, we incorporate physical and geometrical constraints to regularize the velocity field. We reconstruct intermediate surfaces using a modified level-set equation, directly linking our NIR with the velocity field. Experiments show that our method significantly outperforms previous NIR approaches across various scenarios (e.g., noisy, partial, topology-changing, non-isometric shapes) and, for the first time, enables new applications like 4D Kinect sequence upsampling and real-world high-resolution mesh deformation.

Implicit Neural Surface Deformation with Explicit Velocity Fields

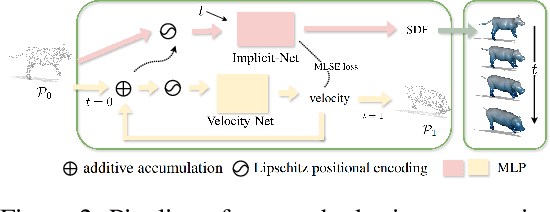
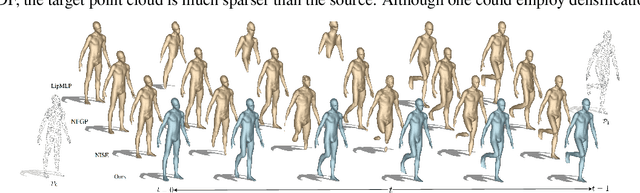
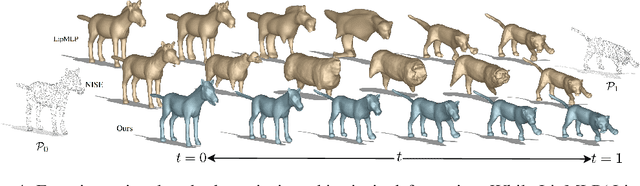
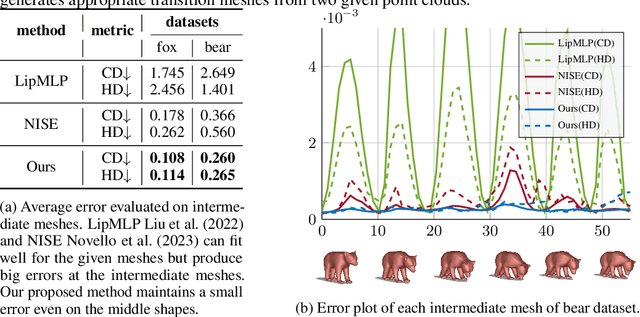
In this work, we introduce the first unsupervised method that simultaneously predicts time-varying neural implicit surfaces and deformations between pairs of point clouds. We propose to model the point movement using an explicit velocity field and directly deform a time-varying implicit field using the modified level-set equation. This equation utilizes an iso-surface evolution with Eikonal constraints in a compact formulation, ensuring the integrity of the signed distance field. By applying a smooth, volume-preserving constraint to the velocity field, our method successfully recovers physically plausible intermediate shapes. Our method is able to handle both rigid and non-rigid deformations without any intermediate shape supervision. Our experimental results demonstrate that our method significantly outperforms existing works, delivering superior results in both quality and efficiency.

Beyond Complete Shapes: A quantitative Evaluation of 3D Shape Matching Algorithms

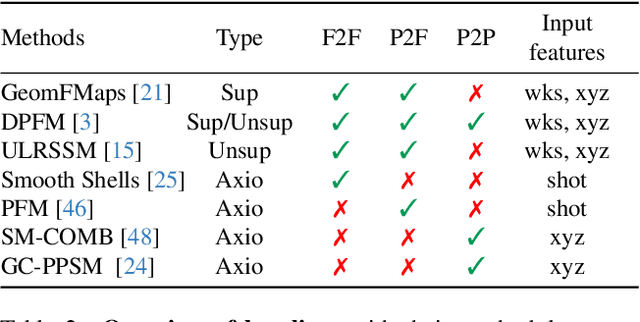
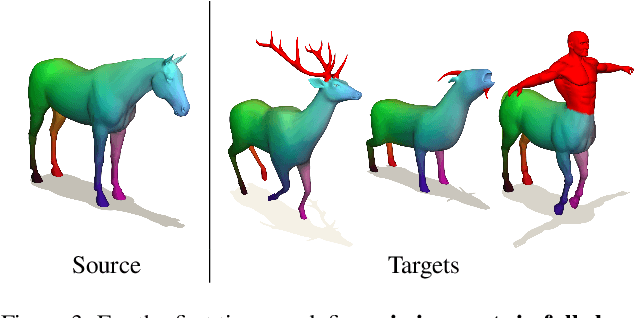
Finding correspondences between 3D shapes is an important and long-standing problem in computer vision, graphics and beyond. While approaches based on machine learning dominate modern 3D shape matching, almost all existing (learning-based) methods require that at least one of the involved shapes is complete. In contrast, the most challenging and arguably most practically relevant setting of matching partially observed shapes, is currently underexplored. One important factor is that existing datasets contain only a small number of shapes (typically below 100), which are unable to serve data-hungry machine learning approaches, particularly in the unsupervised regime. In addition, the type of partiality present in existing datasets is often artificial and far from realistic. To address these limitations and to encourage research on these relevant settings, we provide a generic and flexible framework for the procedural generation of challenging partial shape matching scenarios. Our framework allows for a virtually infinite generation of partial shape matching instances from a finite set of shapes with complete geometry. Further, we manually create cross-dataset correspondences between seven existing (complete geometry) shape matching datasets, leading to a total of 2543 shapes. Based on this, we propose several challenging partial benchmark settings, for which we evaluate respective state-of-the-art methods as baselines.

DiffCD: A Symmetric Differentiable Chamfer Distance for Neural Implicit Surface Fitting

Neural implicit surfaces can be used to recover accurate 3D geometry from imperfect point clouds. In this work, we show that state-of-the-art techniques work by minimizing an approximation of a one-sided Chamfer distance. This shape metric is not symmetric, as it only ensures that the point cloud is near the surface but not vice versa. As a consequence, existing methods can produce inaccurate reconstructions with spurious surfaces. Although one approach against spurious surfaces has been widely used in the literature, we theoretically and experimentally show that it is equivalent to regularizing the surface area, resulting in over-smoothing. As a more appealing alternative, we propose DiffCD, a novel loss function corresponding to the symmetric Chamfer distance. In contrast to previous work, DiffCD also assures that the surface is near the point cloud, which eliminates spurious surfaces without the need for additional regularization. We experimentally show that DiffCD reliably recovers a high degree of shape detail, substantially outperforming existing work across varying surface complexity and noise levels. Project code is available at https://github.com/linusnie/diffcd.

Erasing the Ephemeral: Joint Camera Refinement and Transient Object Removal for Street View Synthesis

Synthesizing novel views for urban environments is crucial for tasks like autonomous driving and virtual tours. Compared to object-level or indoor situations, outdoor settings present unique challenges, such as inconsistency across frames due to moving vehicles and camera pose drift over lengthy sequences. In this paper, we introduce a method that tackles these challenges on view synthesis for outdoor scenarios. We employ a neural point light field scene representation and strategically detect and mask out dynamic objects to reconstruct novel scenes without artifacts. Moreover, we simultaneously optimize camera pose along with the view synthesis process, and thus, we simultaneously refine both elements. Through validation on real-world urban datasets, we demonstrate state-of-the-art results in synthesizing novel views of urban scenes.

Coloring the Past: Neural Historical Buildings Reconstruction from Archival Photography

Historical buildings are a treasure and milestone of human cultural heritage. Reconstructing the 3D models of these building hold significant value. The rapid development of neural rendering methods makes it possible to recover the 3D shape only based on archival photographs. However, this task presents considerable challenges due to the limitations of such datasets. Historical photographs are often limited in number and the scenes in these photos might have altered over time. The radiometric quality of these images is also often sub-optimal. To address these challenges, we introduce an approach to reconstruct the geometry of historical buildings, employing volumetric rendering techniques. We leverage dense point clouds as a geometric prior and introduce a color appearance embedding loss to recover the color of the building given limited available color images. We aim for our work to spark increased interest and focus on preserving historical buildings. Thus, we also introduce a new historical dataset of the Hungarian National Theater, providing a new benchmark for the reconstruction method.

Weight-Aware Implicit Geometry Reconstruction with Curvature-Guided Sampling

Neural surface implicit representations offer numerous advantages, including the ability to easily modify topology and surface resolution. However, reconstructing implicit geometry representation with only limited known data is challenging. In this paper, we present an approach that effectively interpolates and extrapolates within training points, generating additional training data to reconstruct a surface with superior qualitative and quantitative results. We also introduce a technique that efficiently calculates differentiable geometric properties, i.e., mean and Gaussian curvatures, to enhance the sampling process during training. Additionally, we propose a weight-aware implicit neural representation that not only streamlines surface extraction but also extend to non-closed surfaces by depicting non-closed areas as locally degenerated patches, thereby mitigating the drawbacks of the previous assumption in implicit neural representations.

Gradient-SDF: A Semi-Implicit Surface Representation for 3D Reconstruction

We present Gradient-SDF, a novel representation for 3D geometry that combines the advantages of implict and explicit representations. By storing at every voxel both the signed distance field as well as its gradient vector field, we enhance the capability of implicit representations with approaches originally formulated for explicit surfaces. As concrete examples, we show that (1) the Gradient-SDF allows us to perform direct SDF tracking from depth images, using efficient storage schemes like hash maps, and that (2) the Gradient-SDF representation enables us to perform photometric bundle adjustment directly in a voxel representation (without transforming into a point cloud or mesh), naturally a fully implicit optimization of geometry and camera poses and easy geometry upsampling. Experimental results confirm that this leads to significantly sharper reconstructions. Since the overall SDF voxel structure is still respected, the proposed Gradient-SDF is equally suited for (GPU) parallelization as related approaches.