Gradient-SDF: A Semi-Implicit Surface Representation for 3D Reconstruction

We present Gradient-SDF, a novel representation for 3D geometry that combines the advantages of implict and explicit representations. By storing at every voxel both the signed distance field as well as its gradient vector field, we enhance the capability of implicit representations with approaches originally formulated for explicit surfaces. As concrete examples, we show that (1) the Gradient-SDF allows us to perform direct SDF tracking from depth images, using efficient storage schemes like hash maps, and that (2) the Gradient-SDF representation enables us to perform photometric bundle adjustment directly in a voxel representation (without transforming into a point cloud or mesh), naturally a fully implicit optimization of geometry and camera poses and easy geometry upsampling. Experimental results confirm that this leads to significantly sharper reconstructions. Since the overall SDF voxel structure is still respected, the proposed Gradient-SDF is equally suited for (GPU) parallelization as related approaches.

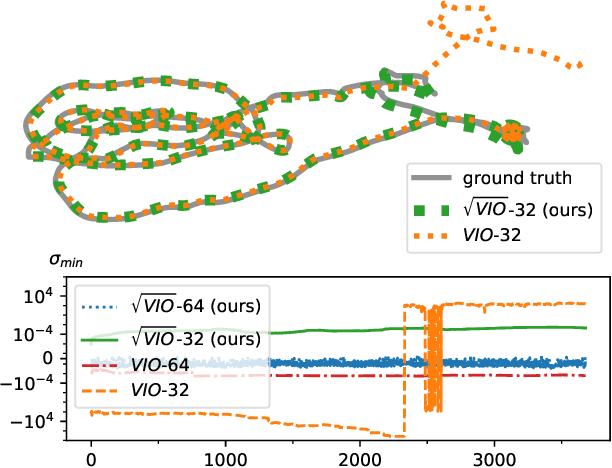
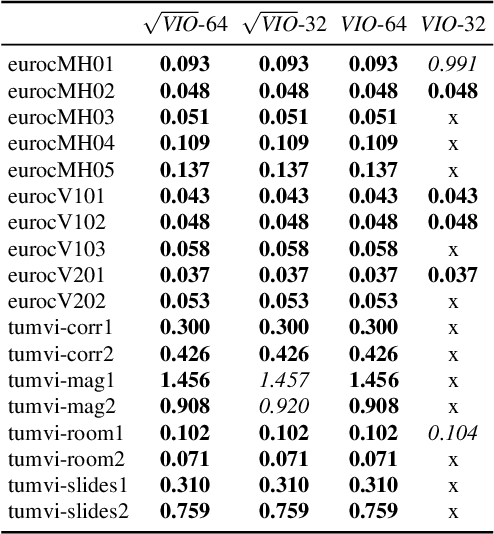
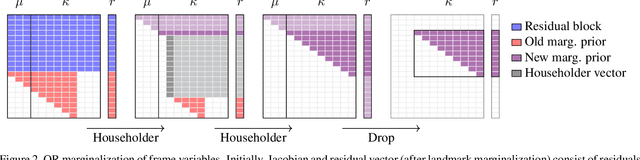
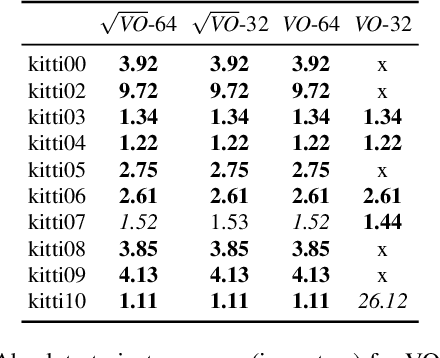
Square Root Marginalization for Sliding-Window Bundle Adjustment

In this paper we propose a novel square root sliding-window bundle adjustment suitable for real-time odometry applications. The square root formulation pervades three major aspects of our optimization-based sliding-window estimator: for bundle adjustment we eliminate landmark variables with nullspace projection; to store the marginalization prior we employ a matrix square root of the Hessian; and when marginalizing old poses we avoid forming normal equations and update the square root prior directly with a specialized QR decomposition. We show that the proposed square root marginalization is algebraically equivalent to the conventional use of Schur complement (SC) on the Hessian. Moreover, it elegantly deals with rank-deficient Jacobians producing a prior equivalent to SC with Moore-Penrose inverse. Our evaluation of visual and visual-inertial odometry on real-world datasets demonstrates that the proposed estimator is 36% faster than the baseline. It furthermore shows that in single precision, conventional Hessian-based marginalization leads to numeric failures and reduced accuracy. We analyse numeric properties of the marginalization prior to explain why our square root form does not suffer from the same effect and therefore entails superior performance.

Square Root Bundle Adjustment for Large-Scale Reconstruction

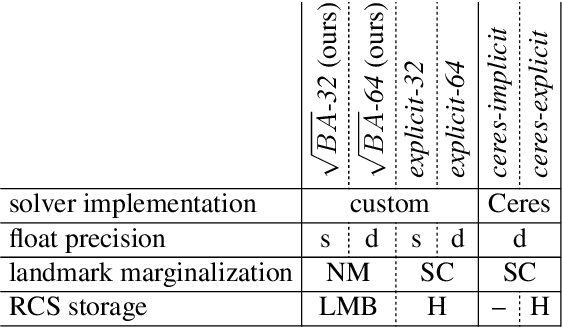
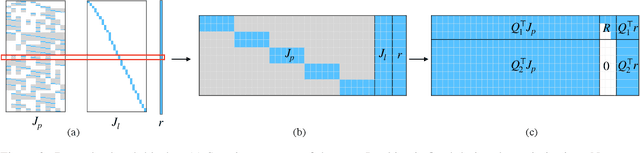
We propose a new formulation for the bundle adjustment problem which relies on nullspace marginalization of landmark variables by QR decomposition. Our approach, which we call square root bundle adjustment, is algebraically equivalent to the commonly used Schur complement trick, improves the numeric stability of computations, and allows for solving large-scale bundle adjustment problems with single-precision floating-point numbers. We show in real-world experiments with the BAL datasets that even in single precision the proposed solver achieves on average equally accurate solutions compared to Schur complement solvers using double precision. It runs significantly faster, but can require larger amounts of memory on dense problems. The proposed formulation relies on simple linear algebra operations and opens the way for efficient implementations of bundle adjustment on hardware platforms optimized for single-precision linear algebra processing.

PrimiTect: Fast Continuous Hough Voting for Primitive Detection

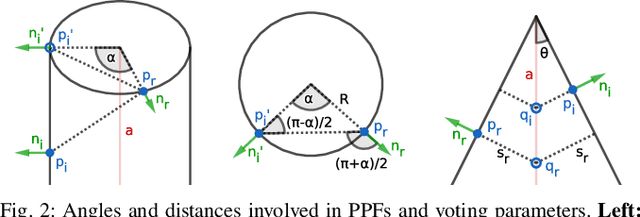
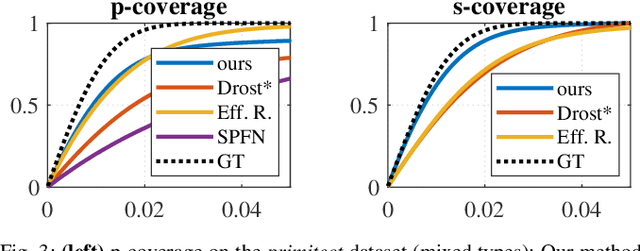
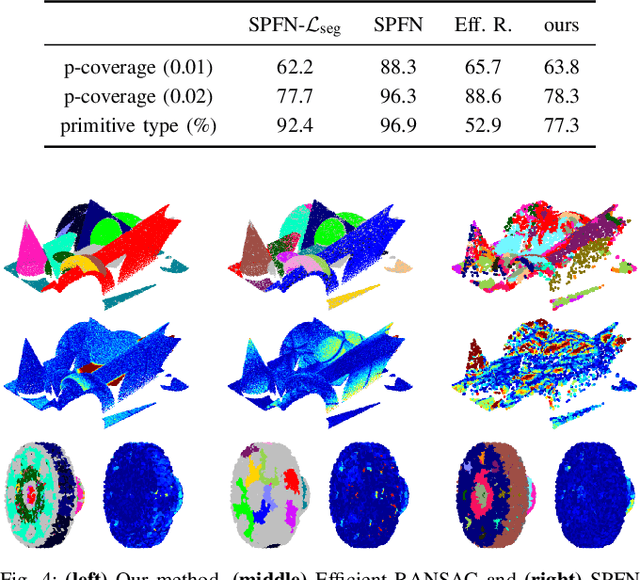
This paper tackles the problem of data abstraction in the context of 3D point sets. Our method classifies points into different geometric primitives, such as planes and cones, leading to a compact representation of the data. Being based on a semi-global Hough voting scheme, the method does not need initialization and is robust, accurate, and efficient. We use a local, low-dimensional parameterization of primitives to determine type, shape and pose of the object that a point belongs to. This makes our algorithm suitable to run on devices with low computational power, as often required in robotics applications. The evaluation shows that our method outperforms state-of-the-art methods both in terms of accuracy and robustness.

From Planes to Corners: Multi-Purpose Primitive Detection in Unorganized 3D Point Clouds

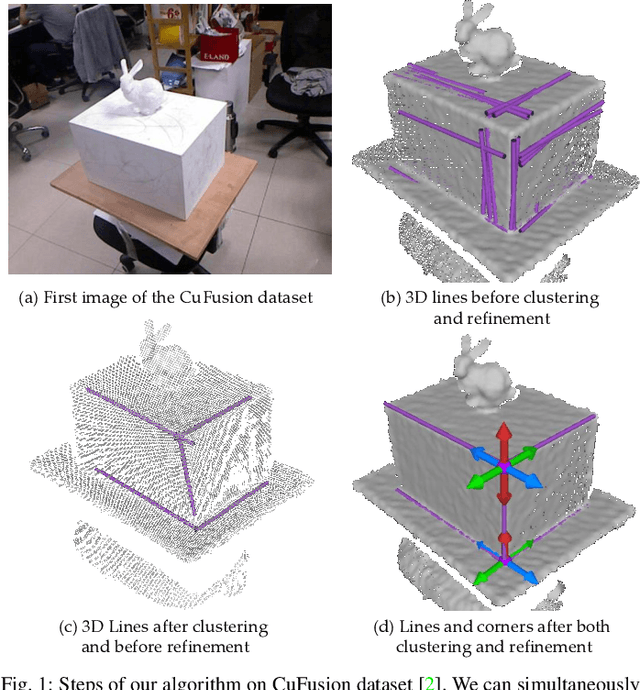
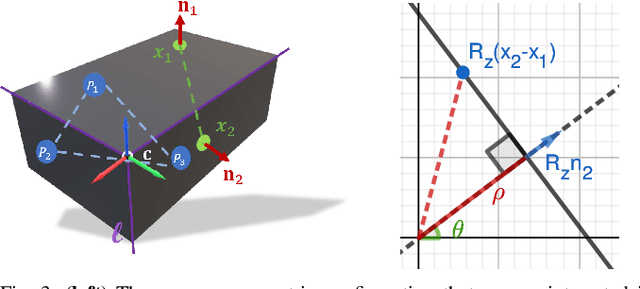
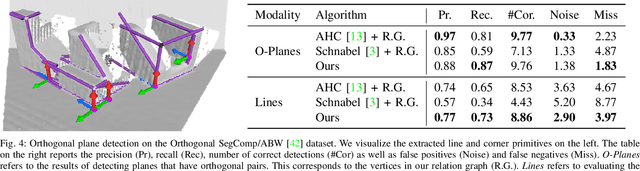
We propose a new method for segmentation-free joint estimation of orthogonal planes, their intersection lines, relationship graph and corners lying at the intersection of three orthogonal planes. Such unified scene exploration under orthogonality allows for multitudes of applications such as semantic plane detection or local and global scan alignment, which in turn can aid robot localization or grasping tasks. Our two-stage pipeline involves a rough yet joint estimation of orthogonal planes followed by a subsequent joint refinement of plane parameters respecting their orthogonality relations. We form a graph of these primitives, paving the way to the extraction of further reliable features: lines and corners. Our experiments demonstrate the validity of our approach in numerous scenarios from wall detection to 6D tracking, both on synthetic and real data.

Efficient Derivative Computation for Cumulative B-Splines on Lie Groups

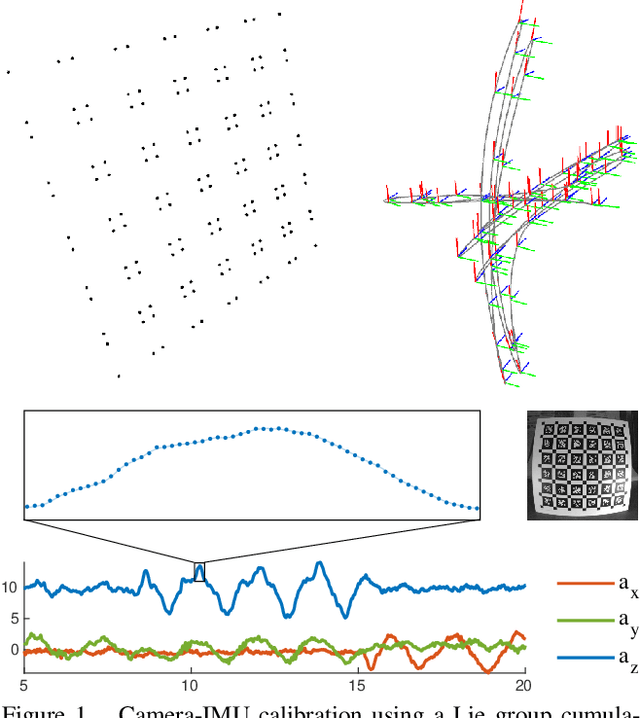
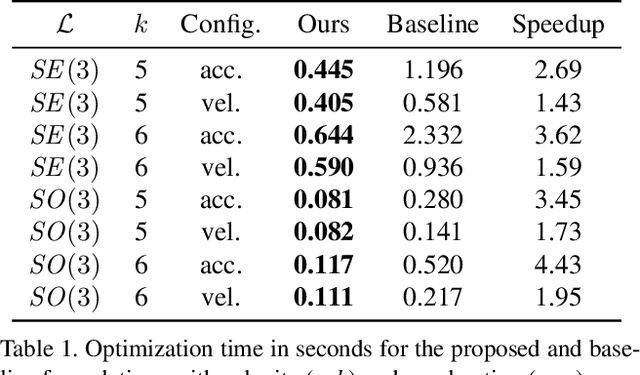
Continuous-time trajectory representation has recently gained popularity for tasks where the fusion of high-frame-rate sensors and multiple unsynchronized devices is required. Lie group cumulative B-splines are a popular way of representing continuous trajectories without singularities. They have been used in near real-time SLAM and odometry systems with IMU, LiDAR, regular, RGB-D and event cameras, as well as for offline calibration. These applications require efficient computation of time derivatives (velocity, acceleration), but all prior works rely on a computationally suboptimal formulation. In this work we present an alternative derivation of time derivatives based on recurrence relations that needs $\mathcal{O}(k)$ instead of $\mathcal{O}(k^2)$ matrix operations (for a spline of order $k$) and results in simple and elegant expressions. While producing the same result, the proposed approach significantly speeds up the trajectory optimization and allows for computing simple analytic derivatives with respect to spline knots. The results presented in this paper pave the way for incorporating continuous-time trajectory representations into more applications where real-time performance is required.