Yumin Sun
PrimiTect: Fast Continuous Hough Voting for Primitive Detection
May 15, 2020
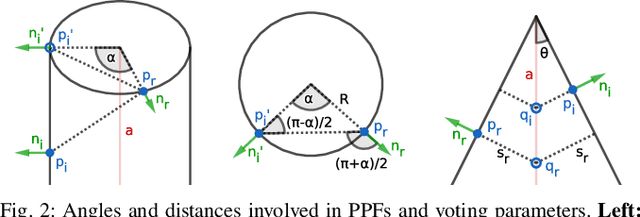
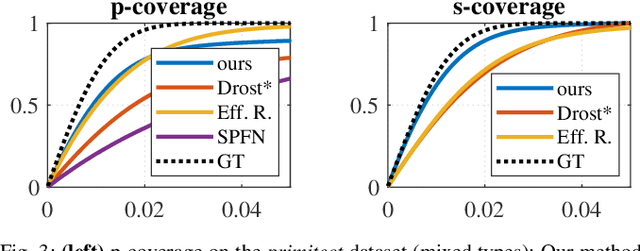
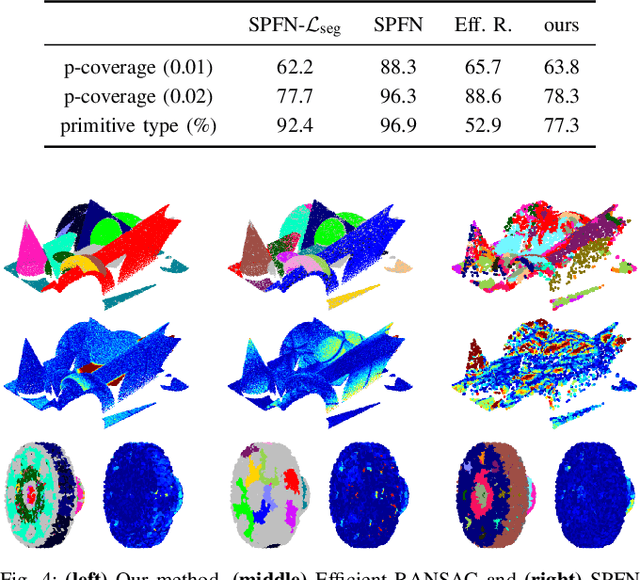
Abstract:This paper tackles the problem of data abstraction in the context of 3D point sets. Our method classifies points into different geometric primitives, such as planes and cones, leading to a compact representation of the data. Being based on a semi-global Hough voting scheme, the method does not need initialization and is robust, accurate, and efficient. We use a local, low-dimensional parameterization of primitives to determine type, shape and pose of the object that a point belongs to. This makes our algorithm suitable to run on devices with low computational power, as often required in robotics applications. The evaluation shows that our method outperforms state-of-the-art methods both in terms of accuracy and robustness.
From Planes to Corners: Multi-Purpose Primitive Detection in Unorganized 3D Point Clouds
Jan 21, 2020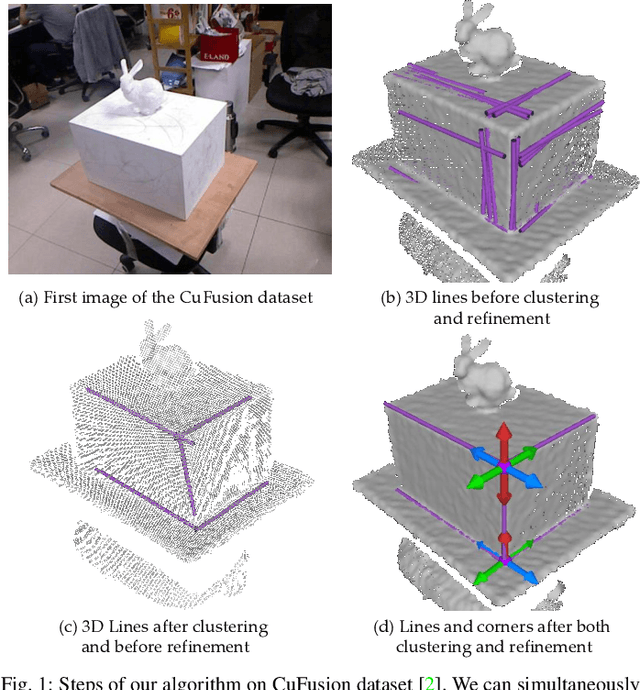

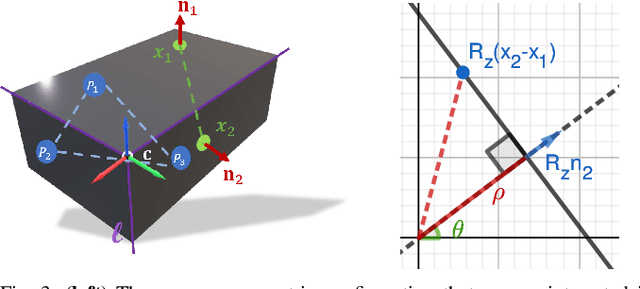
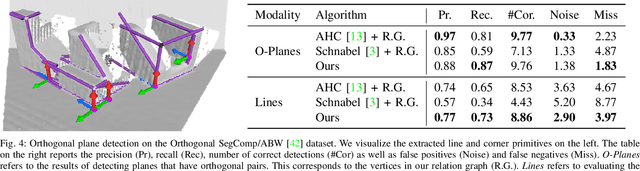
Abstract:We propose a new method for segmentation-free joint estimation of orthogonal planes, their intersection lines, relationship graph and corners lying at the intersection of three orthogonal planes. Such unified scene exploration under orthogonality allows for multitudes of applications such as semantic plane detection or local and global scan alignment, which in turn can aid robot localization or grasping tasks. Our two-stage pipeline involves a rough yet joint estimation of orthogonal planes followed by a subsequent joint refinement of plane parameters respecting their orthogonality relations. We form a graph of these primitives, paving the way to the extraction of further reliable features: lines and corners. Our experiments demonstrate the validity of our approach in numerous scenarios from wall detection to 6D tracking, both on synthetic and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge