DeepShapeMatchingKit: Accelerated Functional Map Solver and Shape Matching Pipelines Revisited

Deep functional maps, leveraging learned feature extractors and spectral correspondence solvers, are fundamental to non-rigid 3D shape matching. Based on an analysis of open-source implementations, we find that standard functional map implementations solve k independent linear systems serially, which is a computational bottleneck at higher spectral resolution. We thus propose a vectorized reformulation that solves all systems in a single kernel call, achieving up to a 33x speedup while preserving the exact solution. Furthermore, we identify and document a previously unnoticed implementation divergence in the spatial gradient features of the mainstay DiffusionNet: two variants that parameterize distinct families of tangent-plane transformations, and present experiments analyzing their respective behaviors across diverse benchmarks. We additionally revisit overlap prediction evaluation for partial-to-partial matching and show that balanced accuracy provides a useful complementary metric under varying overlap ratios. To share these advancements with the wider community, we present an open-source codebase, DeepShapeMatchingKit, that incorporates these improvements and standardizes training, evaluation, and data pipelines for common deep shape matching methods. The codebase is available at: https://github.com/xieyizheng/DeepShapeMatchingKit

Beyond Complete Shapes: A quantitative Evaluation of 3D Shape Matching Algorithms

Finding correspondences between 3D shapes is an important and long-standing problem in computer vision, graphics and beyond. While approaches based on machine learning dominate modern 3D shape matching, almost all existing (learning-based) methods require that at least one of the involved shapes is complete. In contrast, the most challenging and arguably most practically relevant setting of matching partially observed shapes, is currently underexplored. One important factor is that existing datasets contain only a small number of shapes (typically below 100), which are unable to serve data-hungry machine learning approaches, particularly in the unsupervised regime. In addition, the type of partiality present in existing datasets is often artificial and far from realistic. To address these limitations and to encourage research on these relevant settings, we provide a generic and flexible framework for the procedural generation of challenging partial shape matching scenarios. Our framework allows for a virtually infinite generation of partial shape matching instances from a finite set of shapes with complete geometry. Further, we manually create cross-dataset correspondences between seven existing (complete geometry) shape matching datasets, leading to a total of 2543 shapes. Based on this, we propose several challenging partial benchmark settings, for which we evaluate respective state-of-the-art methods as baselines.

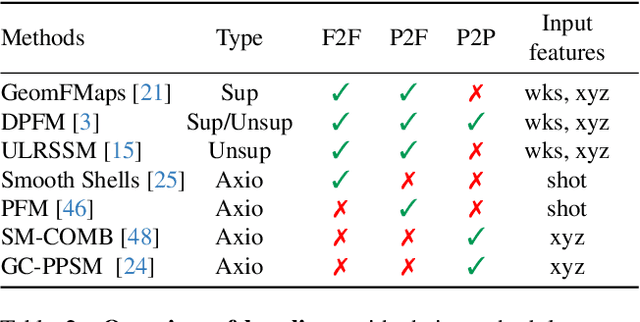
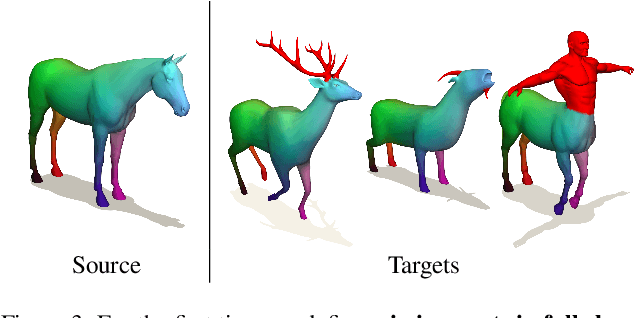
Hybrid Functional Maps for Crease-Aware Non-Isometric Shape Matching

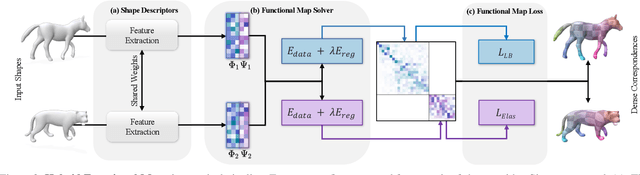
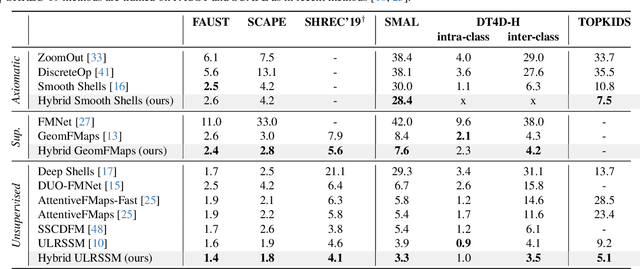
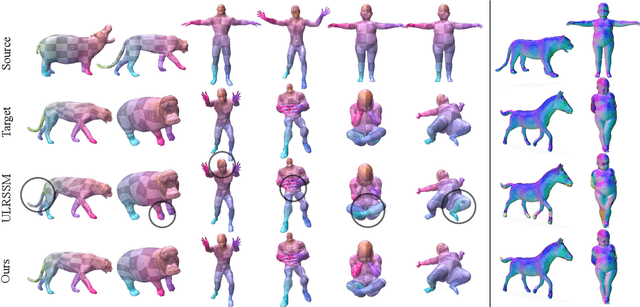
Non-isometric shape correspondence remains a fundamental challenge in computer vision. Traditional methods using Laplace-Beltrami operator (LBO) eigenmodes face limitations in characterizing high-frequency extrinsic shape changes like bending and creases. We propose a novel approach of combining the non-orthogonal extrinsic basis of eigenfunctions of the elastic thin-shell hessian with the intrinsic ones of the LBO, creating a hybrid spectral space in which we construct functional maps. To this end, we present a theoretical framework to effectively integrate non-orthogonal basis functions into descriptor- and learning-based functional map methods. Our approach can be incorporated easily into existing functional map pipelines across varying applications and is able to handle complex deformations beyond isometries. We show extensive evaluations across various supervised and unsupervised settings and demonstrate significant improvements. Notably, our approach achieves up to 15% better mean geodesic error for non-isometric correspondence settings and up to 45% improvement in scenarios with topological noise.