Beyond Complete Shapes: A quantitative Evaluation of 3D Shape Matching Algorithms

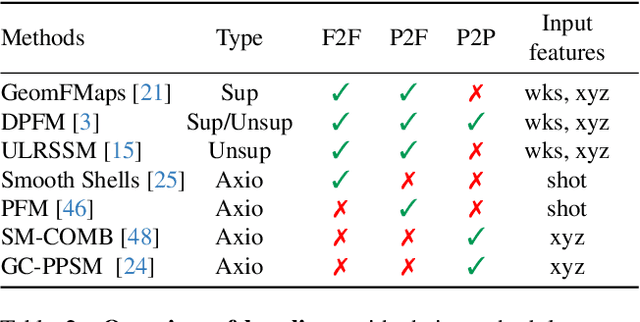
Finding correspondences between 3D shapes is an important and long-standing problem in computer vision, graphics and beyond. While approaches based on machine learning dominate modern 3D shape matching, almost all existing (learning-based) methods require that at least one of the involved shapes is complete. In contrast, the most challenging and arguably most practically relevant setting of matching partially observed shapes, is currently underexplored. One important factor is that existing datasets contain only a small number of shapes (typically below 100), which are unable to serve data-hungry machine learning approaches, particularly in the unsupervised regime. In addition, the type of partiality present in existing datasets is often artificial and far from realistic. To address these limitations and to encourage research on these relevant settings, we provide a generic and flexible framework for the procedural generation of challenging partial shape matching scenarios. Our framework allows for a virtually infinite generation of partial shape matching instances from a finite set of shapes with complete geometry. Further, we manually create cross-dataset correspondences between seven existing (complete geometry) shape matching datasets, leading to a total of 2543 shapes. Based on this, we propose several challenging partial benchmark settings, for which we evaluate respective state-of-the-art methods as baselines.

Partial-to-Partial Shape Matching with Geometric Consistency

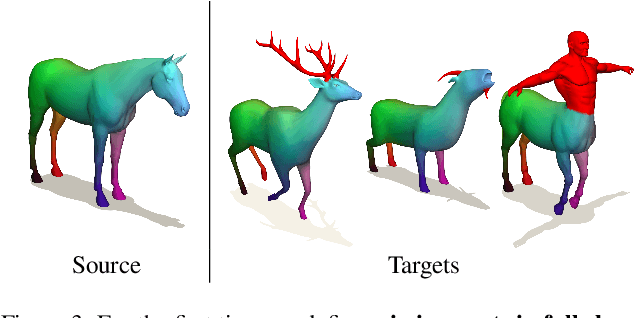
Finding correspondences between 3D shapes is an important and long-standing problem in computer vision, graphics and beyond. A prominent challenge are partial-to-partial shape matching settings, which occur when the shapes to match are only observed incompletely (e.g. from 3D scanning). Although partial-to-partial matching is a highly relevant setting in practice, it is rarely explored. Our work bridges the gap between existing (rather artificial) 3D full shape matching and partial-to-partial real-world settings by exploiting geometric consistency as a strong constraint. We demonstrate that it is indeed possible to solve this challenging problem in a variety of settings. For the first time, we achieve geometric consistency for partial-to-partial matching, which is realized by a novel integer non-linear program formalism building on triangle product spaces, along with a new pruning algorithm based on linear integer programming. Further, we generate a new inter-class dataset for partial-to-partial shape-matching. We show that our method outperforms current SOTA methods on both an established intra-class dataset and our novel inter-class dataset.

Geometrically Consistent Partial Shape Matching

Finding correspondences between 3D shapes is a crucial problem in computer vision and graphics, which is for example relevant for tasks like shape interpolation, pose transfer, or texture transfer. An often neglected but essential property of matchings is geometric consistency, which means that neighboring triangles in one shape are consistently matched to neighboring triangles in the other shape. Moreover, while in practice one often has only access to partial observations of a 3D shape (e.g. due to occlusion, or scanning artifacts), there do not exist any methods that directly address geometrically consistent partial shape matching. In this work we fill this gap by proposing to integrate state-of-the-art deep shape features into a novel integer linear programming partial shape matching formulation. Our optimization yields a globally optimal solution on low resolution shapes, which we then refine using a coarse-to-fine scheme. We show that our method can find more reliable results on partial shapes in comparison to existing geometrically consistent algorithms (for which one first has to fill missing parts with a dummy geometry). Moreover, our matchings are substantially smoother than learning-based state-of-the-art shape matching methods.

Non-Separable Multi-Dimensional Network Flows for Visual Computing

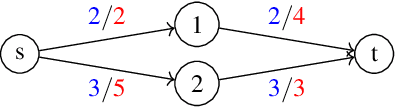
Flows in networks (or graphs) play a significant role in numerous computer vision tasks. The scalar-valued edges in these graphs often lead to a loss of information and thereby to limitations in terms of expressiveness. For example, oftentimes high-dimensional data (e.g. feature descriptors) are mapped to a single scalar value (e.g. the similarity between two feature descriptors). To overcome this limitation, we propose a novel formalism for non-separable multi-dimensional network flows. By doing so, we enable an automatic and adaptive feature selection strategy - since the flow is defined on a per-dimension basis, the maximizing flow automatically chooses the best matching feature dimensions. As a proof of concept, we apply our formalism to the multi-object tracking problem and demonstrate that our approach outperforms scalar formulations on the MOT16 benchmark in terms of robustness to noise.

Shortest Paths in Graphs with Matrix-Valued Edges: Concepts, Algorithm and Application to 3D Multi-Shape Analysis

Finding shortest paths in a graph is relevant for numerous problems in computer vision and graphics, including image segmentation, shape matching, or the computation of geodesic distances on discrete surfaces. Traditionally, the concept of a shortest path is considered for graphs with scalar edge weights, which makes it possible to compute the length of a path by adding up the individual edge weights. Yet, graphs with scalar edge weights are severely limited in their expressivity, since oftentimes edges are used to encode significantly more complex interrelations. In this work we compensate for this modelling limitation and introduce the novel graph-theoretic concept of a shortest path in a graph with matrix-valued edges. To this end, we define a meaningful way for quantifying the path length for matrix-valued edges, and we propose a simple yet effective algorithm to compute the respective shortest path. While our formalism is universal and thus applicable to a wide range of settings in vision, graphics and beyond, we focus on demonstrating its merits in the context of 3D multi-shape analysis.