Fast Globally Optimal and Geometrically Consistent 3D Shape Matching

Geometric consistency, i.e. the preservation of neighbourhoods, is a natural and strong prior in 3D shape matching. Geometrically consistent matchings are crucial for many downstream applications, such as texture transfer or statistical shape modelling. Yet, in practice, geometric consistency is often overlooked, or only achieved under severely limiting assumptions (e.g. a good initialisation). In this work, we propose a novel formalism for computing globally optimal and geometrically consistent matchings between 3D shapes which is scalable in practice. Our key idea is to represent the surface of the source shape as a collection of cyclic paths, which are then consistently matched to the target shape. Mathematically, we construct a hyper product graph (between source and target shape), and then cast 3D shape matching as a minimum-cost circulation flow problem in this hyper graph, which yields global geometrically consistent matchings between both shapes. We empirically show that our formalism is efficiently solvable and that it leads to high-quality results.

Partial-to-Partial Shape Matching with Geometric Consistency

Finding correspondences between 3D shapes is an important and long-standing problem in computer vision, graphics and beyond. A prominent challenge are partial-to-partial shape matching settings, which occur when the shapes to match are only observed incompletely (e.g. from 3D scanning). Although partial-to-partial matching is a highly relevant setting in practice, it is rarely explored. Our work bridges the gap between existing (rather artificial) 3D full shape matching and partial-to-partial real-world settings by exploiting geometric consistency as a strong constraint. We demonstrate that it is indeed possible to solve this challenging problem in a variety of settings. For the first time, we achieve geometric consistency for partial-to-partial matching, which is realized by a novel integer non-linear program formalism building on triangle product spaces, along with a new pruning algorithm based on linear integer programming. Further, we generate a new inter-class dataset for partial-to-partial shape-matching. We show that our method outperforms current SOTA methods on both an established intra-class dataset and our novel inter-class dataset.

Revisiting Map Relations for Unsupervised Non-Rigid Shape Matching

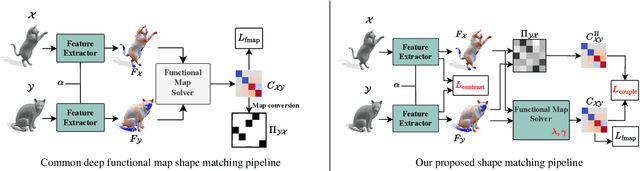
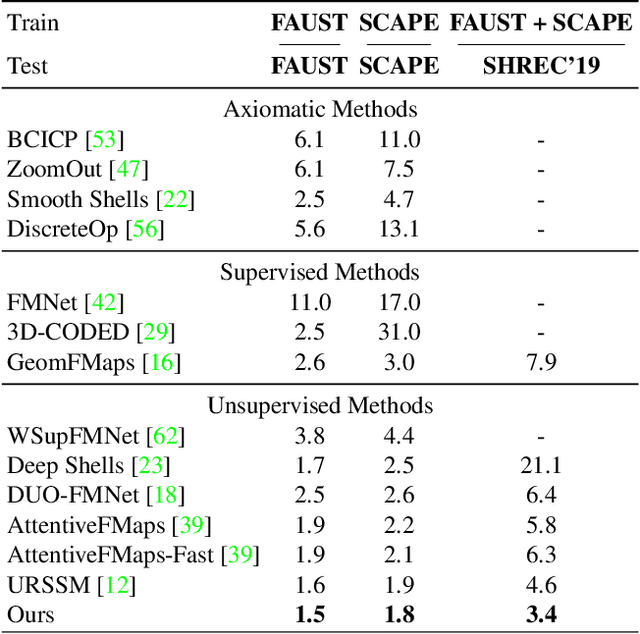
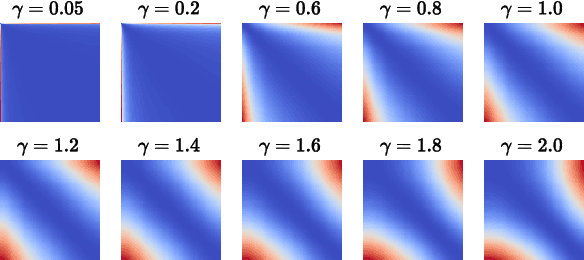
We propose a novel unsupervised learning approach for non-rigid 3D shape matching. Our approach improves upon recent state-of-the art deep functional map methods and can be applied to a broad range of different challenging scenarios. Previous deep functional map methods mainly focus on feature extraction and aim exclusively at obtaining more expressive features for functional map computation. However, the importance of the functional map computation itself is often neglected and the relationship between the functional map and point-wise map is underexplored. In this paper, we systematically investigate the coupling relationship between the functional map from the functional map solver and the point-wise map based on feature similarity. To this end, we propose a self-adaptive functional map solver to adjust the functional map regularisation for different shape matching scenarios, together with a vertex-wise contrastive loss to obtain more discriminative features. Using different challenging datasets (including non-isometry, topological noise and partiality), we demonstrate that our method substantially outperforms previous state-of-the-art methods.

Fast Discrete Optimisation for Geometrically Consistent 3D Shape Matching

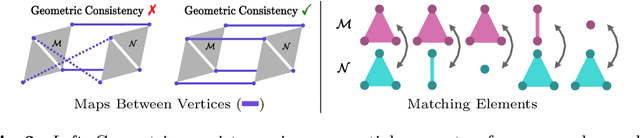
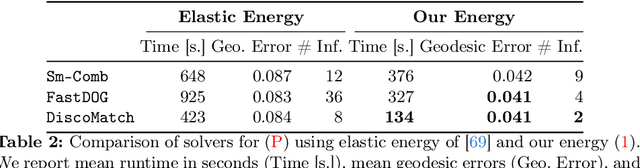
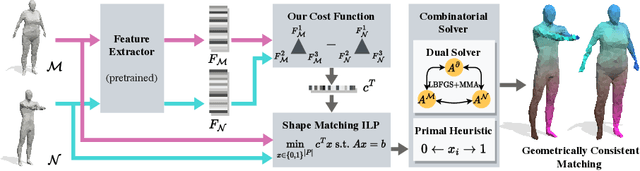
In this work we propose to combine the advantages of learning-based and combinatorial formalisms for 3D shape matching. While learning-based shape matching solutions lead to state-of-the-art matching performance, they do not ensure geometric consistency, so that obtained matchings are locally unsmooth. On the contrary, axiomatic methods allow to take geometric consistency into account by explicitly constraining the space of valid matchings. However, existing axiomatic formalisms are impractical since they do not scale to practically relevant problem sizes, or they require user input for the initialisation of non-convex optimisation problems. In this work we aim to close this gap by proposing a novel combinatorial solver that combines a unique set of favourable properties: our approach is (i) initialisation free, (ii) massively parallelisable powered by a quasi-Newton method, (iii) provides optimality gaps, and (iv) delivers decreased runtime and globally optimal results for many instances.

Geometrically Consistent Partial Shape Matching

Finding correspondences between 3D shapes is a crucial problem in computer vision and graphics, which is for example relevant for tasks like shape interpolation, pose transfer, or texture transfer. An often neglected but essential property of matchings is geometric consistency, which means that neighboring triangles in one shape are consistently matched to neighboring triangles in the other shape. Moreover, while in practice one often has only access to partial observations of a 3D shape (e.g. due to occlusion, or scanning artifacts), there do not exist any methods that directly address geometrically consistent partial shape matching. In this work we fill this gap by proposing to integrate state-of-the-art deep shape features into a novel integer linear programming partial shape matching formulation. Our optimization yields a globally optimal solution on low resolution shapes, which we then refine using a coarse-to-fine scheme. We show that our method can find more reliable results on partial shapes in comparison to existing geometrically consistent algorithms (for which one first has to fill missing parts with a dummy geometry). Moreover, our matchings are substantially smoother than learning-based state-of-the-art shape matching methods.

SIGMA: Scale-Invariant Global Sparse Shape Matching

We propose a novel mixed-integer programming (MIP) formulation for generating precise sparse correspondences for highly non-rigid shapes. To this end, we introduce a projected Laplace-Beltrami operator (PLBO) which combines intrinsic and extrinsic geometric information to measure the deformation quality induced by predicted correspondences. We integrate the PLBO, together with an orientation-aware regulariser, into a novel MIP formulation that can be solved to global optimality for many practical problems. In contrast to previous methods, our approach is provably invariant to rigid transformations and global scaling, initialisation-free, has optimality guarantees, and scales to high resolution meshes with (empirically observed) linear time. We show state-of-the-art results for sparse non-rigid matching on several challenging 3D datasets, including data with inconsistent meshing, as well as applications in mesh-to-point-cloud matching.

Unsupervised Learning of Robust Spectral Shape Matching

We propose a novel learning-based approach for robust 3D shape matching. Our method builds upon deep functional maps and can be trained in a fully unsupervised manner. Previous deep functional map methods mainly focus on predicting optimised functional maps alone, and then rely on off-the-shelf post-processing to obtain accurate point-wise maps during inference. However, this two-stage procedure for obtaining point-wise maps often yields sub-optimal performance. In contrast, building upon recent insights about the relation between functional maps and point-wise maps, we propose a novel unsupervised loss to couple the functional maps and point-wise maps, and thereby directly obtain point-wise maps without any post-processing. Our approach obtains accurate correspondences not only for near-isometric shapes, but also for more challenging non-isometric shapes and partial shapes, as well as shapes with different discretisation or topological noise. Using a total of nine diverse datasets, we extensively evaluate the performance and demonstrate that our method substantially outperforms previous state-of-the-art methods, even compared to recent supervised methods. Our code is available at https://github.com/dongliangcao/Unsupervised-Learning-of-Robust-Spectral-Shape-Matching.

Conjugate Product Graphs for Globally Optimal 2D-3D Shape Matching

We consider the problem of finding a continuous and non-rigid matching between a 2D contour and a 3D mesh. While such problems can be solved to global optimality by finding a shortest path in the product graph between both shapes, existing solutions heavily rely on unrealistic prior assumptions to avoid degenerate solutions (e.g. knowledge to which region of the 3D shape each point of the 2D contour is matched). To address this, we propose a novel 2D-3D shape matching formalism based on the conjugate product graph between the 2D contour and the 3D shape. Doing so allows us for the first time to consider higher-order costs, i.e. defined for edge chains, as opposed to costs defined for single edges. This offers substantially more flexibility, which we utilise to incorporate a local rigidity prior. By doing so, we effectively circumvent degenerate solutions and thereby obtain smoother and more realistic matchings, even when using only a one-dimensional feature descriptor. Overall, our method finds globally optimal and continuous 2D-3D matchings, has the same asymptotic complexity as previous solutions, produces state-of-the-art results for shape matching and is even capable of matching partial shapes.

A Scalable Combinatorial Solver for Elastic Geometrically Consistent 3D Shape Matching

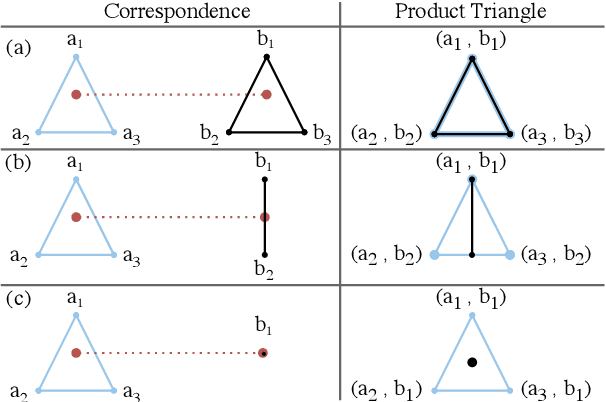
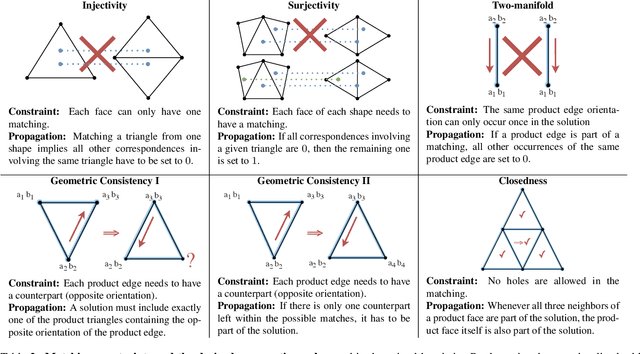
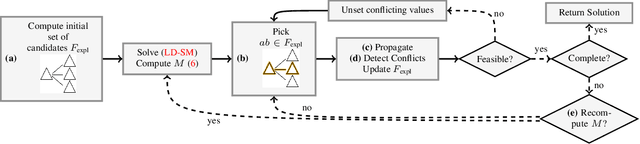
We present a scalable combinatorial algorithm for globally optimizing over the space of geometrically consistent mappings between 3D shapes. We use the mathematically elegant formalism proposed by Windheuser et al. (ICCV 2011) where 3D shape matching was formulated as an integer linear program over the space of orientation-preserving diffeomorphisms. Until now, the resulting formulation had limited practical applicability due to its complicated constraint structure and its large size. We propose a novel primal heuristic coupled with a Lagrange dual problem that is several orders of magnitudes faster compared to previous solvers. This allows us to handle shapes with substantially more triangles than previously solvable. We demonstrate compelling results on diverse datasets, and, even showcase that we can address the challenging setting of matching two partial shapes without availability of complete shapes. Our code is publicly available at http://github.com/paul0noah/sm-comb .

Structured Prediction Problem Archive

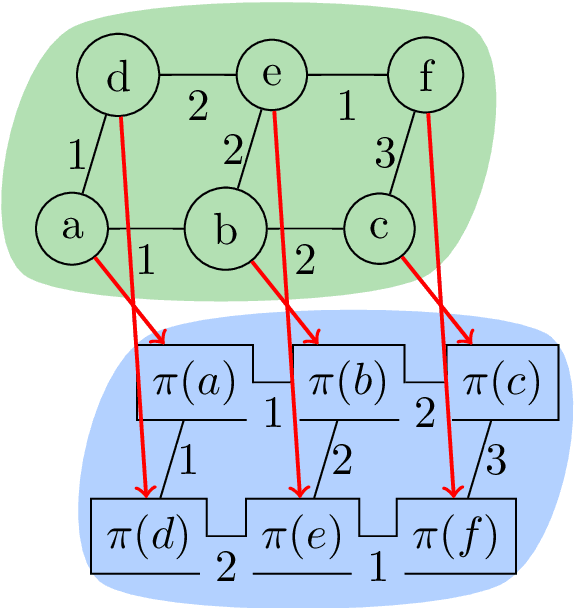
Structured prediction problems are one of the fundamental tools in machine learning. In order to facilitate algorithm development for their numerical solution, we collect in one place a large number of datasets in easy to read formats for a diverse set of problem classes. We provide archival links to datasets, description of the considered problems and problem formats, and a short summary of problem characteristics including size, number of instances etc. For reference we also give a non-exhaustive selection of algorithms proposed in the literature for their solution. We hope that this central repository will make benchmarking and comparison to established works easier. We welcome submission of interesting new datasets and algorithms for inclusion in our archive.