Structured Prediction Problem Archive

Structured prediction problems are one of the fundamental tools in machine learning. In order to facilitate algorithm development for their numerical solution, we collect in one place a large number of datasets in easy to read formats for a diverse set of problem classes. We provide archival links to datasets, description of the considered problems and problem formats, and a short summary of problem characteristics including size, number of instances etc. For reference we also give a non-exhaustive selection of algorithms proposed in the literature for their solution. We hope that this central repository will make benchmarking and comparison to established works easier. We welcome submission of interesting new datasets and algorithms for inclusion in our archive.

Making Higher Order MOT Scalable: An Efficient Approximate Solver for Lifted Disjoint Paths

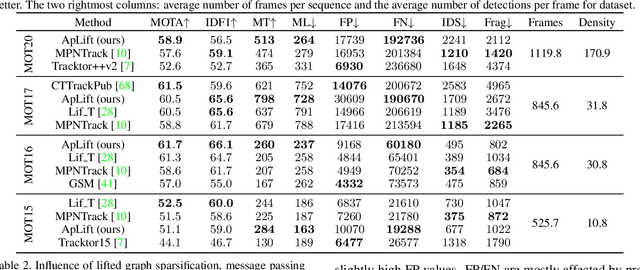
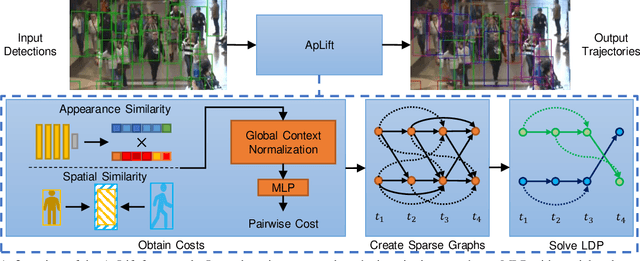
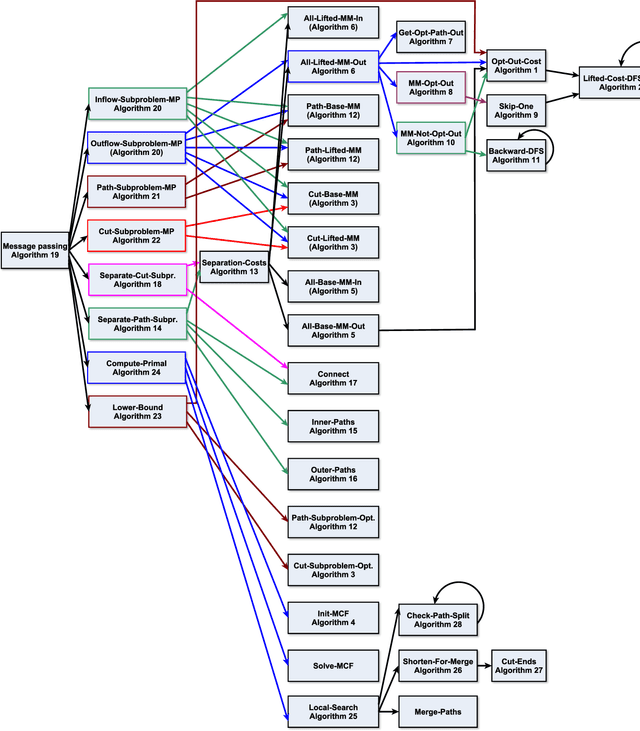
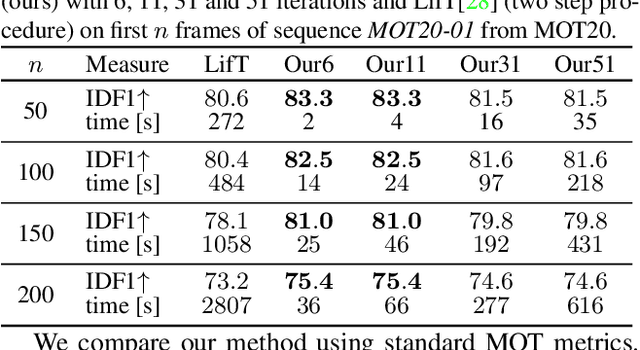
We present an efficient approximate message passing solver for the lifted disjoint paths problem (LDP), a natural but NP-hard model for multiple object tracking (MOT). Our tracker scales to very large instances that come from long and crowded MOT sequences. Our approximate solver enables us to process the MOT15/16/17 benchmarks without sacrificing solution quality and allows for solving MOT20, which has been out of reach up to now for LDP solvers due to its size and complexity. On all these four standard MOT benchmarks we achieve performance comparable or better than current state-of-the-art methods including a tracker based on an optimal LDP solver.

Lifted Disjoint Paths with Application in Multiple Object Tracking

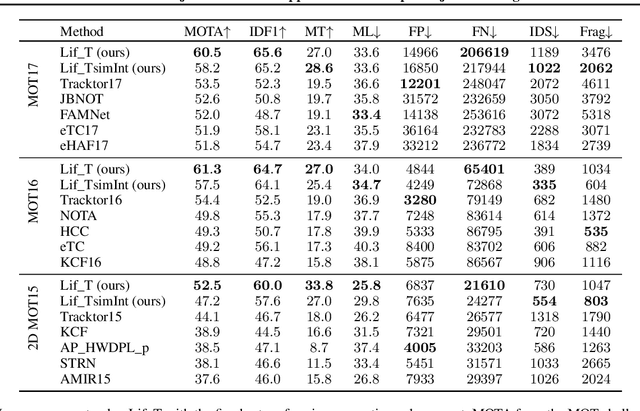
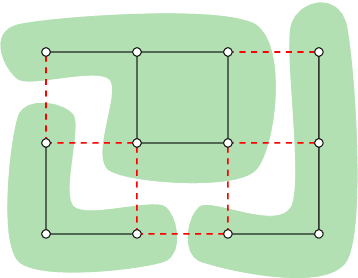
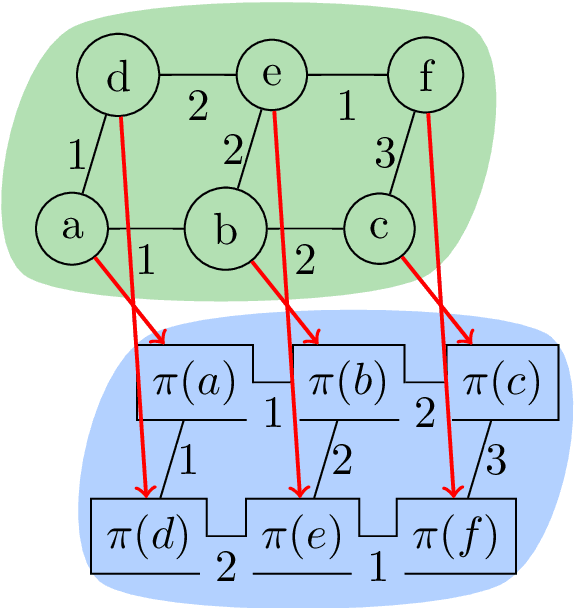
We present an extension to the disjoint paths problem in which additional \emph{lifted} edges are introduced to provide path connectivity priors. We call the resulting optimization problem the lifted disjoint paths problem. We show that this problem is NP-hard by reduction from integer multicommodity flow and 3-SAT. To enable practical global optimization, we propose several classes of linear inequalities that produce a high-quality LP-relaxation. Additionally, we propose efficient cutting plane algorithms for separating the proposed linear inequalities. The lifted disjoint path problem is a natural model for multiple object tracking and allows an elegant mathematical formulation for long range temporal interactions. Lifted edges help to prevent id switches and to re-identify persons. Our lifted disjoint paths tracker achieves nearly optimal assignments with respect to input detections. As a consequence, it leads on all three main benchmarks of the MOT challenge, improving significantly over state-of-the-art.