Ahmed Abbas
Max Planck Institute for Informatics, Saarbrücken
LiteTracker: Leveraging Temporal Causality for Accurate Low-latency Tissue Tracking
Apr 14, 2025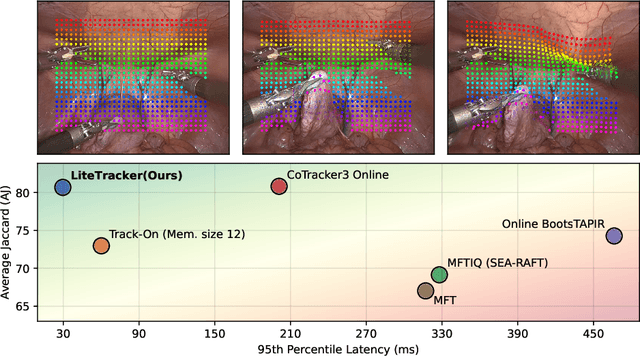
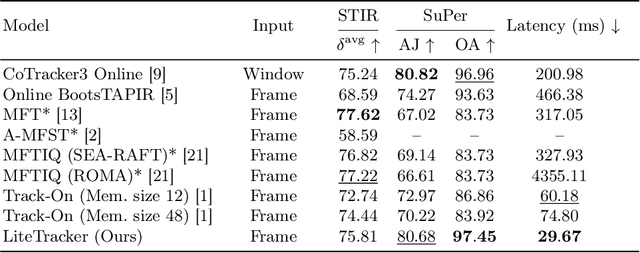
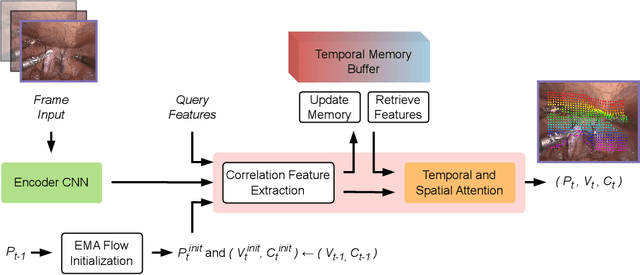

Abstract:Tissue tracking plays a critical role in various surgical navigation and extended reality (XR) applications. While current methods trained on large synthetic datasets achieve high tracking accuracy and generalize well to endoscopic scenes, their runtime performances fail to meet the low-latency requirements necessary for real-time surgical applications. To address this limitation, we propose LiteTracker, a low-latency method for tissue tracking in endoscopic video streams. LiteTracker builds on a state-of-the-art long-term point tracking method, and introduces a set of training-free runtime optimizations. These optimizations enable online, frame-by-frame tracking by leveraging a temporal memory buffer for efficient feature reuse and utilizing prior motion for accurate track initialization. LiteTracker demonstrates significant runtime improvements being around 7x faster than its predecessor and 2x than the state-of-the-art. Beyond its primary focus on efficiency, LiteTracker delivers high-accuracy tracking and occlusion prediction, performing competitively on both the STIR and SuPer datasets. We believe LiteTracker is an important step toward low-latency tissue tracking for real-time surgical applications in the operating room.
Fast Discrete Optimisation for Geometrically Consistent 3D Shape Matching
Oct 12, 2023
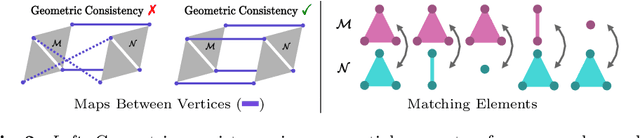
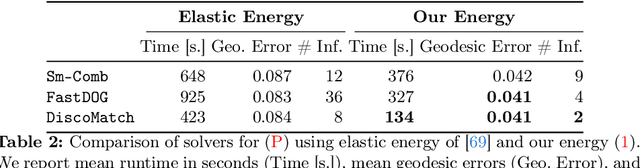
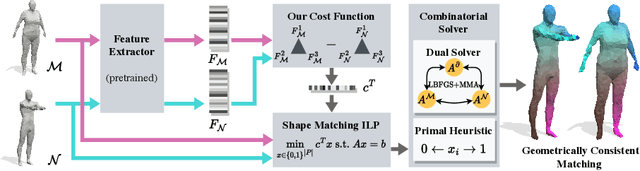
Abstract:In this work we propose to combine the advantages of learning-based and combinatorial formalisms for 3D shape matching. While learning-based shape matching solutions lead to state-of-the-art matching performance, they do not ensure geometric consistency, so that obtained matchings are locally unsmooth. On the contrary, axiomatic methods allow to take geometric consistency into account by explicitly constraining the space of valid matchings. However, existing axiomatic formalisms are impractical since they do not scale to practically relevant problem sizes, or they require user input for the initialisation of non-convex optimisation problems. In this work we aim to close this gap by proposing a novel combinatorial solver that combines a unique set of favourable properties: our approach is (i) initialisation free, (ii) massively parallelisable powered by a quasi-Newton method, (iii) provides optimality gaps, and (iv) delivers decreased runtime and globally optimal results for many instances.
ClusterFuG: Clustering Fully connected Graphs by Multicut
Jan 28, 2023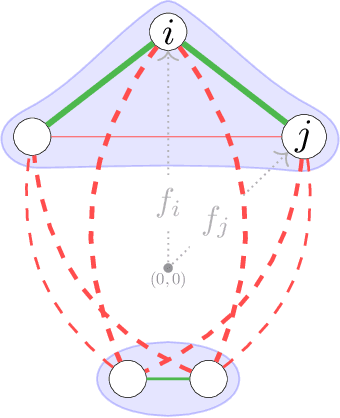
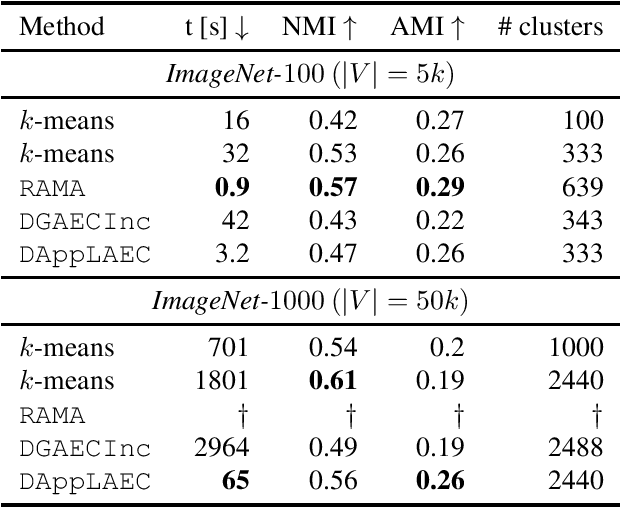
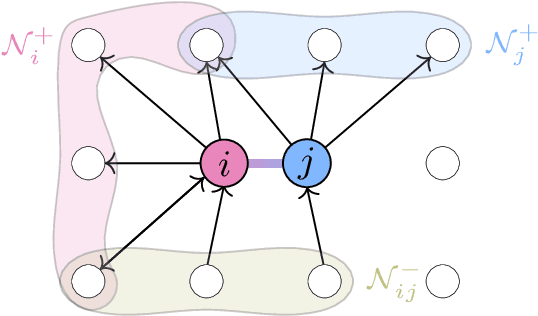
Abstract:We propose a graph clustering formulation based on multicut (a.k.a. weighted correlation clustering) on the complete graph. Our formulation does not need specification of the graph topology as in the original sparse formulation of multicut, making our approach simpler and potentially better performing. In contrast to unweighted correlation clustering we allow for a more expressive weighted cost structure. In dense multicut, the clustering objective is given in a factorized form as inner products of node feature vectors. This allows for an efficient formulation and inference in contrast to multicut/weighted correlation clustering, which has at least quadratic representation and computation complexity when working on the complete graph. We show how to rewrite classical greedy algorithms for multicut in our dense setting and how to modify them for greater efficiency and solution quality. In particular, our algorithms scale to graphs with tens of thousands of nodes. Empirical evidence on instance segmentation on Cityscapes and clustering of ImageNet datasets shows the merits of our approach.
DOGE-Train: Discrete Optimization on GPU with End-to-end Training
May 23, 2022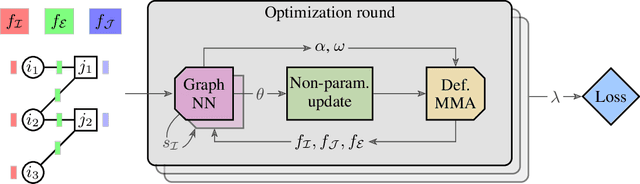

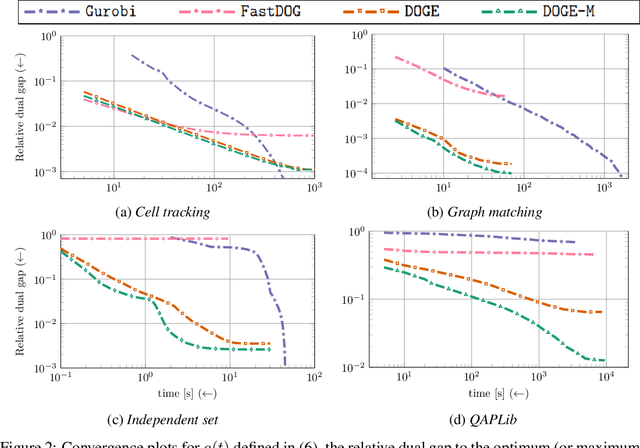
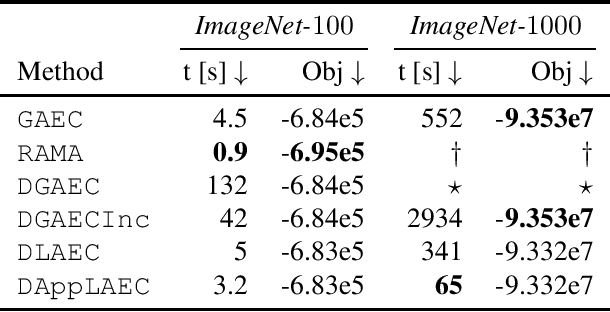
Abstract:We present a fast, scalable, data-driven approach for solving linear relaxations of 0-1 integer linear programs using a graph neural network. Our solver is based on the Lagrange decomposition based algorithm FastDOG (Abbas et al. (2022)). We make the algorithm differentiable and perform backpropagation through the dual update scheme for end-to-end training of its algorithmic parameters. This allows to preserve the algorithm's theoretical properties including feasibility and guaranteed non-decrease in the lower bound. Since FastDOG can get stuck in suboptimal fixed points, we provide additional freedom to our graph neural network to predict non-parametric update steps for escaping such points while maintaining dual feasibility. For training of the graph neural network we use an unsupervised loss and perform experiments on large-scale real world datasets. We train on smaller problems and test on larger ones showing strong generalization performance with a graph neural network comprising only around 10k parameters. Our solver achieves significantly faster performance and better dual objectives than its non-learned version. In comparison to commercial solvers our learned solver achieves close to optimal objective values of LP relaxations and is faster by up to an order of magnitude on very large problems from structured prediction and on selected combinatorial optimization problems.
Structured Prediction Problem Archive
Feb 04, 2022
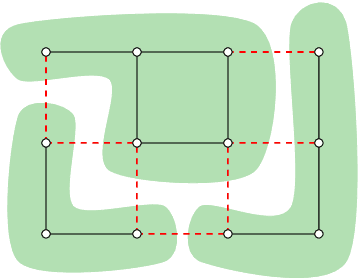

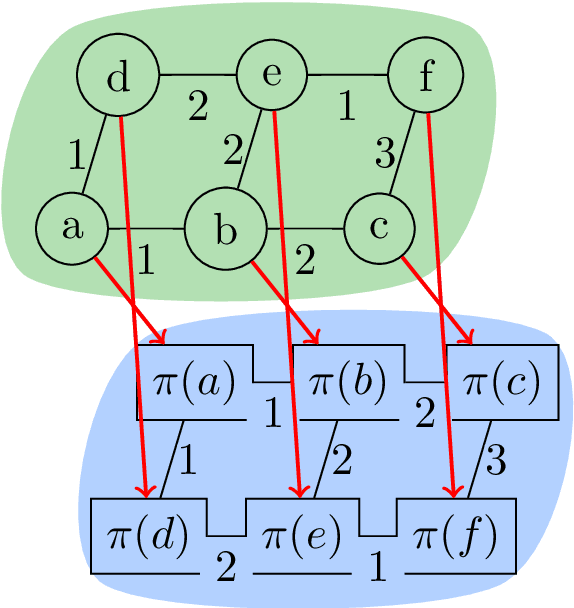
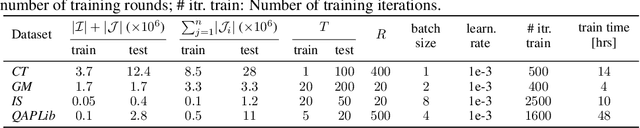
Abstract:Structured prediction problems are one of the fundamental tools in machine learning. In order to facilitate algorithm development for their numerical solution, we collect in one place a large number of datasets in easy to read formats for a diverse set of problem classes. We provide archival links to datasets, description of the considered problems and problem formats, and a short summary of problem characteristics including size, number of instances etc. For reference we also give a non-exhaustive selection of algorithms proposed in the literature for their solution. We hope that this central repository will make benchmarking and comparison to established works easier. We welcome submission of interesting new datasets and algorithms for inclusion in our archive.
FastDOG: Fast Discrete Optimization on GPU
Nov 19, 2021

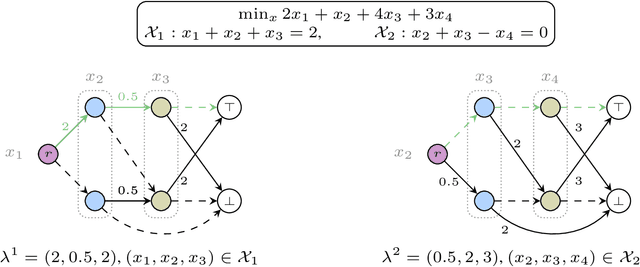
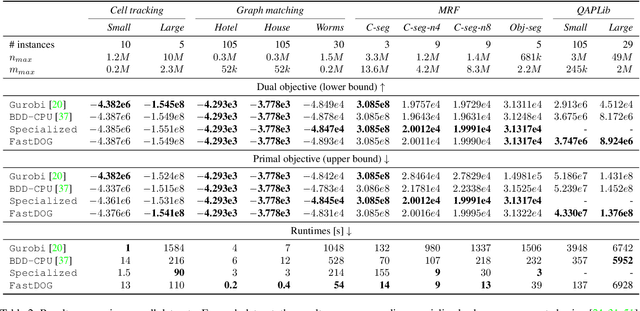
Abstract:We present a massively parallel Lagrange decomposition method for solving 0-1 integer linear programs occurring in structured prediction. We propose a new iterative update scheme for solving the Lagrangean dual and a perturbation technique for decoding primal solutions. For representing subproblems we follow Lange et al. (2021) and use binary decision diagrams (BDDs). Our primal and dual algorithms require little synchronization between subproblems and optimization over BDDs needs only elementary operations without complicated control flow. This allows us to exploit the parallelism offered by GPUs for all components of our method. We present experimental results on combinatorial problems from MAP inference for Markov Random Fields, quadratic assignment and cell tracking for developmental biology. Our highly parallel GPU implementation improves upon the running times of the algorithms from Lange et al. (2021) by up to an order of magnitude. In particular, we come close to or outperform some state-of-the-art specialized heuristics while being problem agnostic.
RAMA: A Rapid Multicut Algorithm on GPU
Sep 04, 2021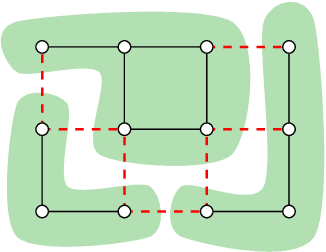
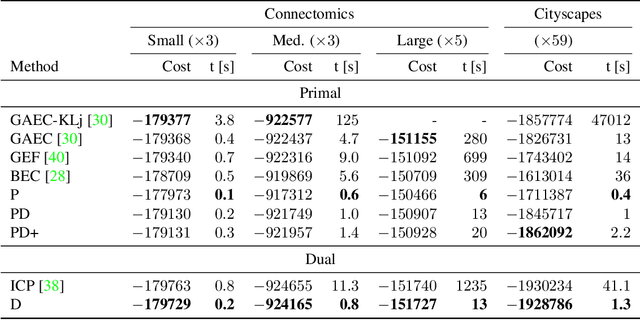
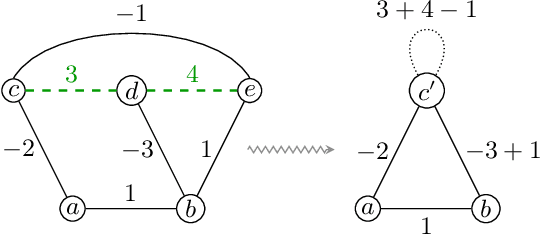
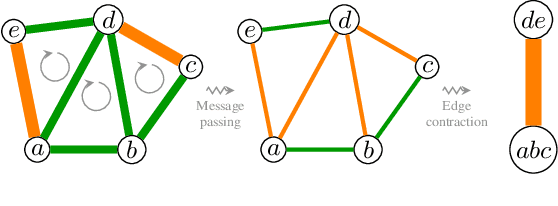
Abstract:We propose a highly parallel primal-dual algorithm for the multicut (a.k.a. correlation clustering) problem, a classical graph clustering problem widely used in machine learning and computer vision. Our algorithm consists of three steps executed recursively: (1) Finding conflicted cycles that correspond to violated inequalities of the underlying multicut relaxation, (2) Performing message passing between the edges and cycles to optimize the Lagrange relaxation coming from the found violated cycles producing reduced costs and (3) Contracting edges with high reduced costs through matrix-matrix multiplications. Our algorithm produces primal solutions and dual lower bounds that estimate the distance to optimum. We implement our algorithm on GPUs and show resulting one to two order-of-magnitudes improvements in execution speed without sacrificing solution quality compared to traditional serial algorithms that run on CPUs. We can solve very large scale benchmark problems with up to $\mathcal{O}(10^8)$ variables in a few seconds with small primal-dual gaps. We make our code available at https://github.com/pawelswoboda/RAMA.
Combinatorial Optimization for Panoptic Segmentation: An End-to-End Trainable Approach
Jun 06, 2021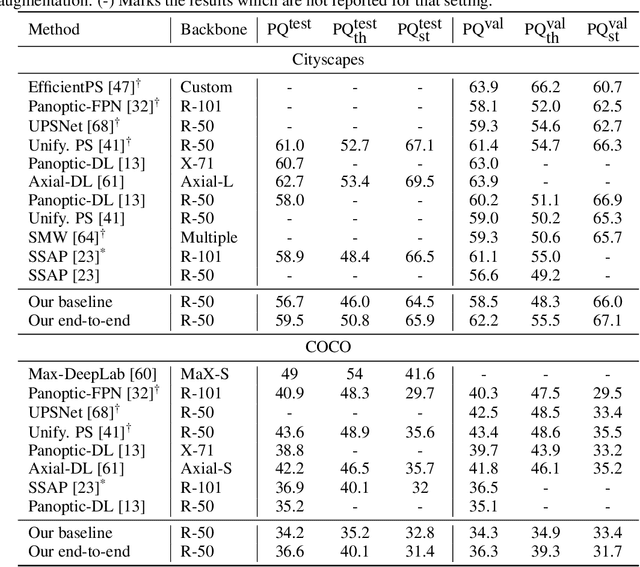
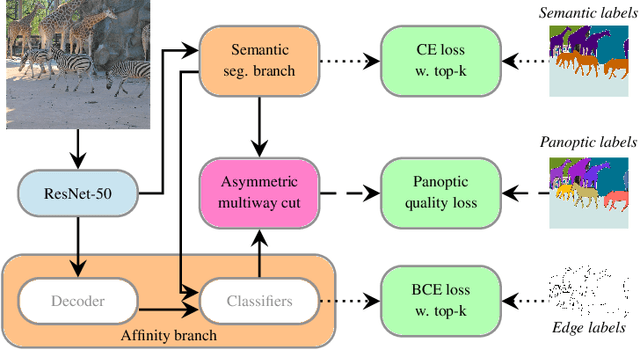

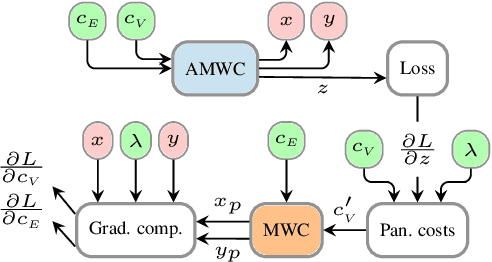
Abstract:We propose an end-to-end trainable architecture for simultaneous semantic and instance segmentation (a.k.a. panoptic segmentation) consisting of a convolutional neural network and an asymmetric multiway cut problem solver. The latter solves a combinatorial optimization problem that elegantly incorporates semantic and boundary predictions to produce a panoptic labeling. Our formulation allows to directly maximize a smooth surrogate of the panoptic quality metric by backpropagating the gradient through the optimization problem. Experimental evaluation shows improvement of end-to-end learning w.r.t. comparable approaches on Cityscapes and COCO datasets. Overall, our approach shows the utility of using combinatorial optimization in tandem with deep learning in a challenging large scale real-world problem and showcases benefits and insights into training such an architecture end-to-end.
Bottleneck potentials in Markov Random Fields
Apr 17, 2019
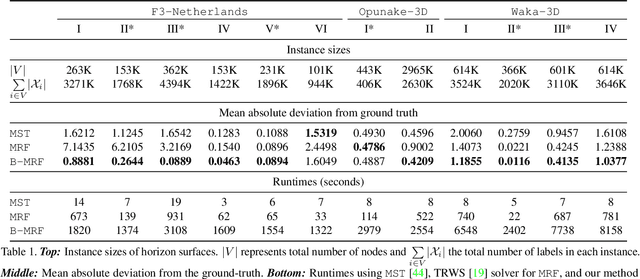
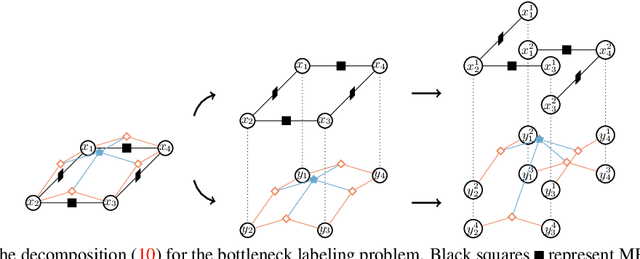
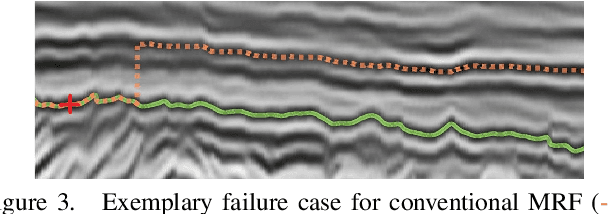
Abstract:We consider general discrete Markov Random Fields(MRFs) with additional bottleneck potentials which penalize the maximum (instead of the sum) over local potential value taken by the MRF-assignment. Bottleneck potentials or analogous constructions have been considered in (i) combinatorial optimization (e.g. bottleneck shortest path problem, the minimum bottleneck spanning tree problem, bottleneck function minimization in greedoids), (ii) inverse problems with $L_{\infty}$-norm regularization, and (iii) valued constraint satisfaction on the $(\min,\max)$-pre-semirings. Bottleneck potentials for general discrete MRFs are a natural generalization of the above direction of modeling work to Maximum-A-Posteriori (MAP) inference in MRFs. To this end, we propose MRFs whose objective consists of two parts: terms that factorize according to (i) $(\min,+)$, i.e. potentials as in plain MRFs, and (ii) $(\min,\max)$, i.e. bottleneck potentials. To solve the ensuing inference problem, we propose high-quality relaxations and efficient algorithms for solving them. We empirically show efficacy of our approach on large scale seismic horizon tracking problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge