DOGE-Train: Discrete Optimization on GPU with End-to-end Training

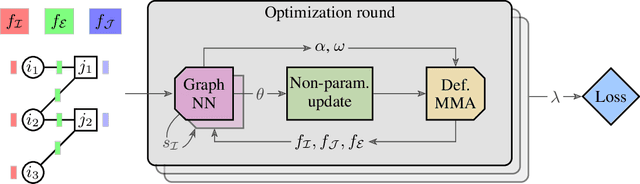
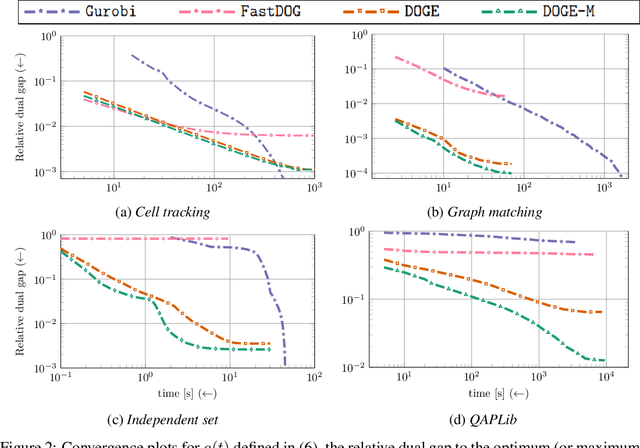
We present a fast, scalable, data-driven approach for solving linear relaxations of 0-1 integer linear programs using a graph neural network. Our solver is based on the Lagrange decomposition based algorithm FastDOG (Abbas et al. (2022)). We make the algorithm differentiable and perform backpropagation through the dual update scheme for end-to-end training of its algorithmic parameters. This allows to preserve the algorithm's theoretical properties including feasibility and guaranteed non-decrease in the lower bound. Since FastDOG can get stuck in suboptimal fixed points, we provide additional freedom to our graph neural network to predict non-parametric update steps for escaping such points while maintaining dual feasibility. For training of the graph neural network we use an unsupervised loss and perform experiments on large-scale real world datasets. We train on smaller problems and test on larger ones showing strong generalization performance with a graph neural network comprising only around 10k parameters. Our solver achieves significantly faster performance and better dual objectives than its non-learned version. In comparison to commercial solvers our learned solver achieves close to optimal objective values of LP relaxations and is faster by up to an order of magnitude on very large problems from structured prediction and on selected combinatorial optimization problems.