PRaDA: Projective Radial Distortion Averaging

We tackle the problem of automatic calibration of radially distorted cameras in challenging conditions. Accurately determining distortion parameters typically requires either 1) solving the full Structure from Motion (SfM) problem involving camera poses, 3D points, and the distortion parameters, which is only possible if many images with sufficient overlap are provided, or 2) relying heavily on learning-based methods that are comparatively less accurate. In this work, we demonstrate that distortion calibration can be decoupled from 3D reconstruction, maintaining the accuracy of SfM-based methods while avoiding many of the associated complexities. This is achieved by working in Projective Space, where the geometry is unique up to a homography, which encapsulates all camera parameters except for distortion. Our proposed method, Projective Radial Distortion Averaging, averages multiple distortion estimates in a fully projective framework without creating 3d points and full bundle adjustment. By relying on pairwise projective relations, our methods support any feature-matching approaches without constructing point tracks across multiple images.

Semantic Library Adaptation: LoRA Retrieval and Fusion for Open-Vocabulary Semantic Segmentation

Open-vocabulary semantic segmentation models associate vision and text to label pixels from an undefined set of classes using textual queries, providing versatile performance on novel datasets. However, large shifts between training and test domains degrade their performance, requiring fine-tuning for effective real-world applications. We introduce Semantic Library Adaptation (SemLA), a novel framework for training-free, test-time domain adaptation. SemLA leverages a library of LoRA-based adapters indexed with CLIP embeddings, dynamically merging the most relevant adapters based on proximity to the target domain in the embedding space. This approach constructs an ad-hoc model tailored to each specific input without additional training. Our method scales efficiently, enhances explainability by tracking adapter contributions, and inherently protects data privacy, making it ideal for sensitive applications. Comprehensive experiments on a 20-domain benchmark built over 10 standard datasets demonstrate SemLA's superior adaptability and performance across diverse settings, establishing a new standard in domain adaptation for open-vocabulary semantic segmentation.

DiffCD: A Symmetric Differentiable Chamfer Distance for Neural Implicit Surface Fitting

Neural implicit surfaces can be used to recover accurate 3D geometry from imperfect point clouds. In this work, we show that state-of-the-art techniques work by minimizing an approximation of a one-sided Chamfer distance. This shape metric is not symmetric, as it only ensures that the point cloud is near the surface but not vice versa. As a consequence, existing methods can produce inaccurate reconstructions with spurious surfaces. Although one approach against spurious surfaces has been widely used in the literature, we theoretically and experimentally show that it is equivalent to regularizing the surface area, resulting in over-smoothing. As a more appealing alternative, we propose DiffCD, a novel loss function corresponding to the symmetric Chamfer distance. In contrast to previous work, DiffCD also assures that the surface is near the point cloud, which eliminates spurious surfaces without the need for additional regularization. We experimentally show that DiffCD reliably recovers a high degree of shape detail, substantially outperforming existing work across varying surface complexity and noise levels. Project code is available at https://github.com/linusnie/diffcd.

To Adapt or Not to Adapt? Real-Time Adaptation for Semantic Segmentation

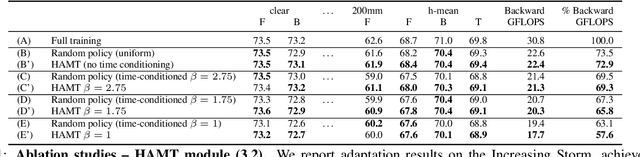
The goal of Online Domain Adaptation for semantic segmentation is to handle unforeseeable domain changes that occur during deployment, like sudden weather events. However, the high computational costs associated with brute-force adaptation make this paradigm unfeasible for real-world applications. In this paper we propose HAMLET, a Hardware-Aware Modular Least Expensive Training framework for real-time domain adaptation. Our approach includes a hardware-aware back-propagation orchestration agent (HAMT) and a dedicated domain-shift detector that enables active control over when and how the model is adapted (LT). Thanks to these advancements, our approach is capable of performing semantic segmentation while simultaneously adapting at more than 29FPS on a single consumer-grade GPU. Our framework's encouraging accuracy and speed trade-off is demonstrated on OnDA and SHIFT benchmarks through experimental results.

Semidefinite Relaxations for Robust Multiview Triangulation

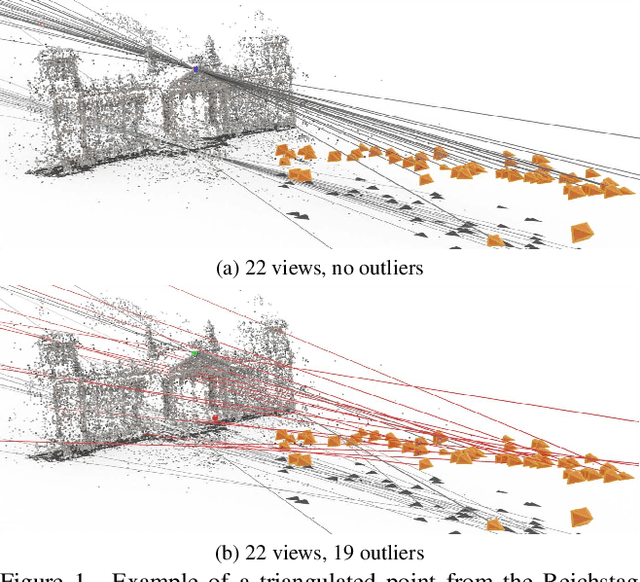
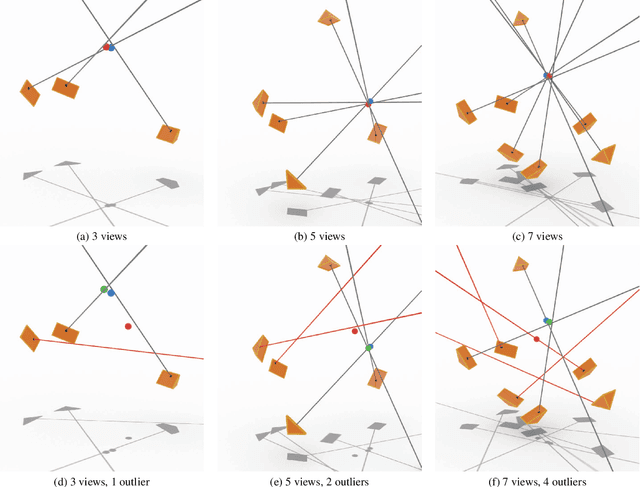
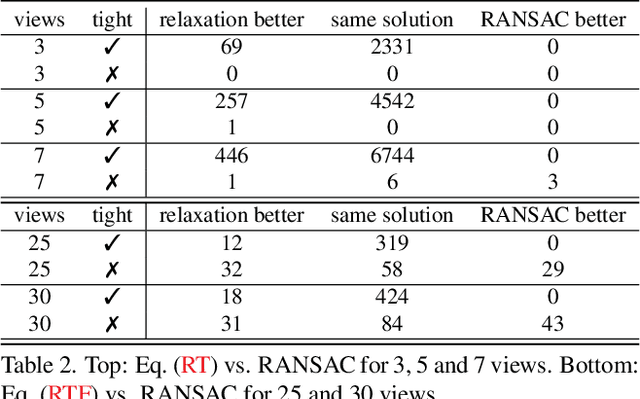
We propose the first convex relaxation for multiview triangulation that is robust to both noise and outliers. To this end, we extend existing semidefinite relaxation approaches to loss functions that include a truncated least squares cost to account for outliers. We propose two formulations, one based on epipolar constraints and one based on the fractional reprojection equations. The first is lower dimensional and remains tight under moderate noise and outlier levels, while the second is higher dimensional and therefore slower but remains tight even under extreme noise and outlier levels. We demonstrate through extensive experiments that the proposed approach allows us to compute provably optimal reconstructions and that empirically the relaxations remain tight even under significant noise and a large percentage of outliers.

Online Domain Adaptation for Semantic Segmentation in Ever-Changing Conditions

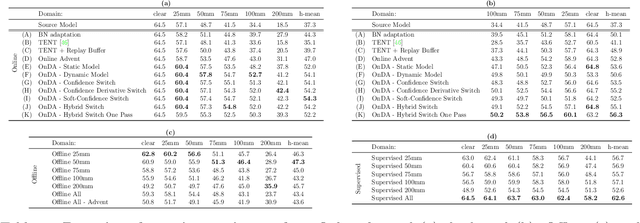
Unsupervised Domain Adaptation (UDA) aims at reducing the domain gap between training and testing data and is, in most cases, carried out in offline manner. However, domain changes may occur continuously and unpredictably during deployment (e.g. sudden weather changes). In such conditions, deep neural networks witness dramatic drops in accuracy and offline adaptation may not be enough to contrast it. In this paper, we tackle Online Domain Adaptation (OnDA) for semantic segmentation. We design a pipeline that is robust to continuous domain shifts, either gradual or sudden, and we evaluate it in the case of rainy and foggy scenarios. Our experiments show that our framework can effectively adapt to new domains during deployment, while not being affected by catastrophic forgetting of the previous domains.

Optimal least-squares solution to the hand-eye calibration problem

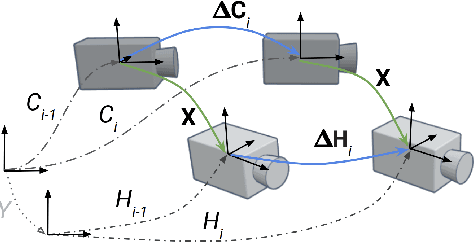
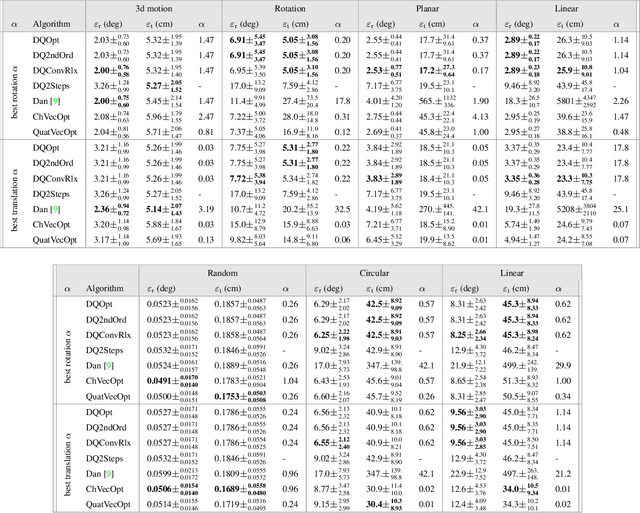
We propose a least-squares formulation to the noisy hand-eye calibration problem using dual-quaternions, and introduce efficient algorithms to find the exact optimal solution, based on analytic properties of the problem, avoiding non-linear optimization. We further present simple analytic approximate solutions which provide remarkably good estimations compared to the exact solution. In addition, we show how to generalize our solution to account for a given extrinsic prior in the cost function. To the best of our knowledge our algorithm is the most efficient approach to optimally solve the hand-eye calibration problem.