Nonisotropic Gaussian Diffusion for Realistic 3D Human Motion Prediction

Probabilistic human motion prediction aims to forecast multiple possible future movements from past observations. While current approaches report high diversity and realism, they often generate motions with undetected limb stretching and jitter. To address this, we introduce SkeletonDiffusion, a latent diffusion model that embeds an explicit inductive bias on the human body within its architecture and training. Our model is trained with a novel nonisotropic Gaussian diffusion formulation that aligns with the natural kinematic structure of the human skeleton. Results show that our approach outperforms conventional isotropic alternatives, consistently generating realistic predictions while avoiding artifacts such as limb distortion. Additionally, we identify a limitation in commonly used diversity metrics, which may inadvertently favor models that produce inconsistent limb lengths within the same sequence. SkeletonDiffusion sets a new benchmark on three real-world datasets, outperforming various baselines across multiple evaluation metrics. Visit our project page: https://ceveloper.github.io/publications/skeletondiffusion/

ZDySS -- Zero-Shot Dynamic Scene Stylization using Gaussian Splatting

Stylizing a dynamic scene based on an exemplar image is critical for various real-world applications, including gaming, filmmaking, and augmented and virtual reality. However, achieving consistent stylization across both spatial and temporal dimensions remains a significant challenge. Most existing methods are designed for static scenes and often require an optimization process for each style image, limiting their adaptability. We introduce ZDySS, a zero-shot stylization framework for dynamic scenes, allowing our model to generalize to previously unseen style images at inference. Our approach employs Gaussian splatting for scene representation, linking each Gaussian to a learned feature vector that renders a feature map for any given view and timestamp. By applying style transfer on the learned feature vectors instead of the rendered feature map, we enhance spatio-temporal consistency across frames. Our method demonstrates superior performance and coherence over state-of-the-art baselines in tests on real-world dynamic scenes, making it a robust solution for practical applications.

DiffCD: A Symmetric Differentiable Chamfer Distance for Neural Implicit Surface Fitting

Neural implicit surfaces can be used to recover accurate 3D geometry from imperfect point clouds. In this work, we show that state-of-the-art techniques work by minimizing an approximation of a one-sided Chamfer distance. This shape metric is not symmetric, as it only ensures that the point cloud is near the surface but not vice versa. As a consequence, existing methods can produce inaccurate reconstructions with spurious surfaces. Although one approach against spurious surfaces has been widely used in the literature, we theoretically and experimentally show that it is equivalent to regularizing the surface area, resulting in over-smoothing. As a more appealing alternative, we propose DiffCD, a novel loss function corresponding to the symmetric Chamfer distance. In contrast to previous work, DiffCD also assures that the surface is near the point cloud, which eliminates spurious surfaces without the need for additional regularization. We experimentally show that DiffCD reliably recovers a high degree of shape detail, substantially outperforming existing work across varying surface complexity and noise levels. Project code is available at https://github.com/linusnie/diffcd.

Gaussian Splatting in Style

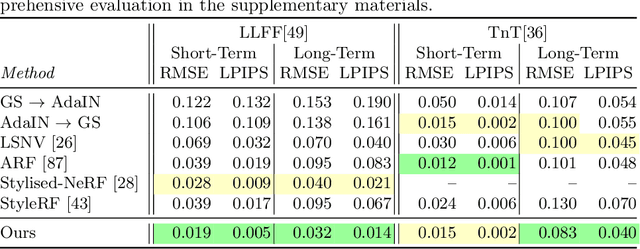
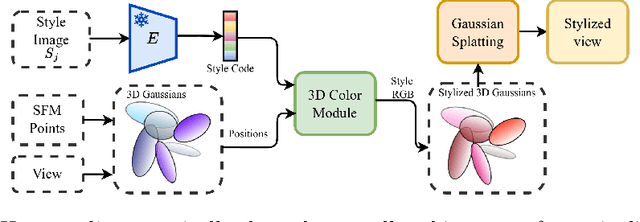
Scene stylization extends the work of neural style transfer to three spatial dimensions. A vital challenge in this problem is to maintain the uniformity of the stylized appearance across a multi-view setting. A vast majority of the previous works achieve this by optimizing the scene with a specific style image. In contrast, we propose a novel architecture trained on a collection of style images, that at test time produces high quality stylized novel views. Our work builds up on the framework of 3D Gaussian splatting. For a given scene, we take the pretrained Gaussians and process them using a multi resolution hash grid and a tiny MLP to obtain the conditional stylised views. The explicit nature of 3D Gaussians give us inherent advantages over NeRF-based methods including geometric consistency, along with having a fast training and rendering regime. This enables our method to be useful for vast practical use cases such as in augmented or virtual reality applications. Through our experiments, we show our methods achieve state-of-the-art performance with superior visual quality on various indoor and outdoor real-world data.

ResolvNet: A Graph Convolutional Network with multi-scale Consistency

It is by now a well known fact in the graph learning community that the presence of bottlenecks severely limits the ability of graph neural networks to propagate information over long distances. What so far has not been appreciated is that, counter-intuitively, also the presence of strongly connected sub-graphs may severely restrict information flow in common architectures. Motivated by this observation, we introduce the concept of multi-scale consistency. At the node level this concept refers to the retention of a connected propagation graph even if connectivity varies over a given graph. At the graph-level, multi-scale consistency refers to the fact that distinct graphs describing the same object at different resolutions should be assigned similar feature vectors. As we show, both properties are not satisfied by poular graph neural network architectures. To remedy these shortcomings, we introduce ResolvNet, a flexible graph neural network based on the mathematical concept of resolvents. We rigorously establish its multi-scale consistency theoretically and verify it in extensive experiments on real world data: Here networks based on this ResolvNet architecture prove expressive; out-performing baselines significantly on many tasks; in- and outside the multi-scale setting.

Weight-Aware Implicit Geometry Reconstruction with Curvature-Guided Sampling

Neural surface implicit representations offer numerous advantages, including the ability to easily modify topology and surface resolution. However, reconstructing implicit geometry representation with only limited known data is challenging. In this paper, we present an approach that effectively interpolates and extrapolates within training points, generating additional training data to reconstruct a surface with superior qualitative and quantitative results. We also introduce a technique that efficiently calculates differentiable geometric properties, i.e., mean and Gaussian curvatures, to enhance the sampling process during training. Additionally, we propose a weight-aware implicit neural representation that not only streamlines surface extraction but also extend to non-closed surfaces by depicting non-closed areas as locally degenerated patches, thereby mitigating the drawbacks of the previous assumption in implicit neural representations.

Implicit Shape Completion via Adversarial Shape Priors

We present a novel neural implicit shape method for partial point cloud completion. To that end, we combine a conditional Deep-SDF architecture with learned, adversarial shape priors. More specifically, our network converts partial inputs into a global latent code and then recovers the full geometry via an implicit, signed distance generator. Additionally, we train a PointNet++ discriminator that impels the generator to produce plausible, globally consistent reconstructions. In that way, we effectively decouple the challenges of predicting shapes that are both realistic, i.e. imitate the training set's pose distribution, and accurate in the sense that they replicate the partial input observations. In our experiments, we demonstrate state-of-the-art performance for completing partial shapes, considering both man-made objects (e.g. airplanes, chairs, ...) and deformable shape categories (human bodies). Finally, we show that our adversarial training approach leads to visually plausible reconstructions that are highly consistent in recovering missing parts of a given object.

FPGA Implementation of Minimum Mean Brightness Error Bi-Histogram Equalization

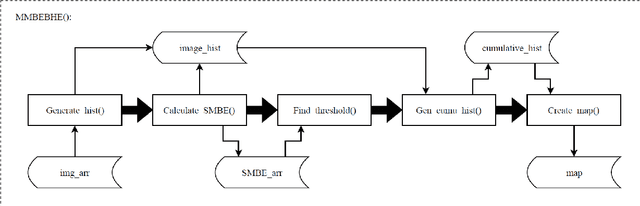
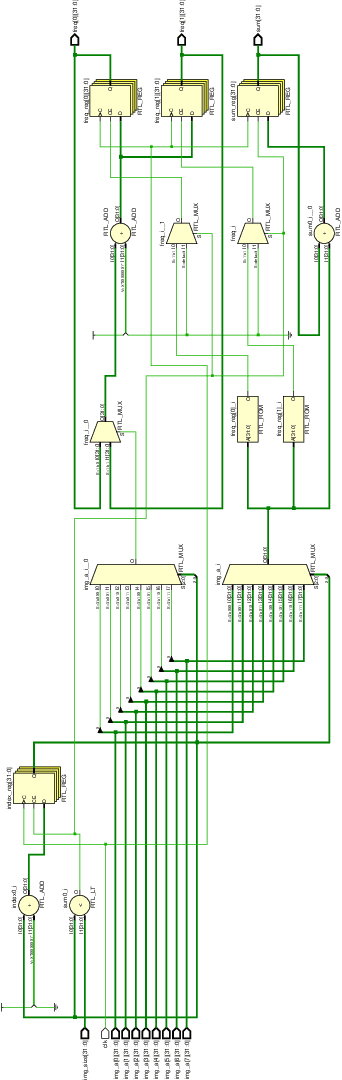
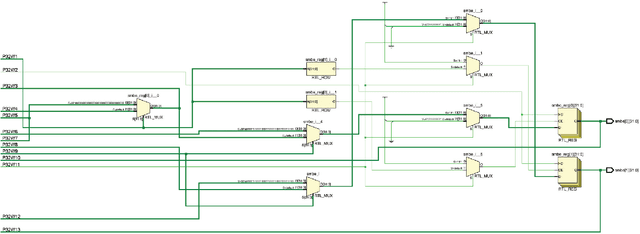
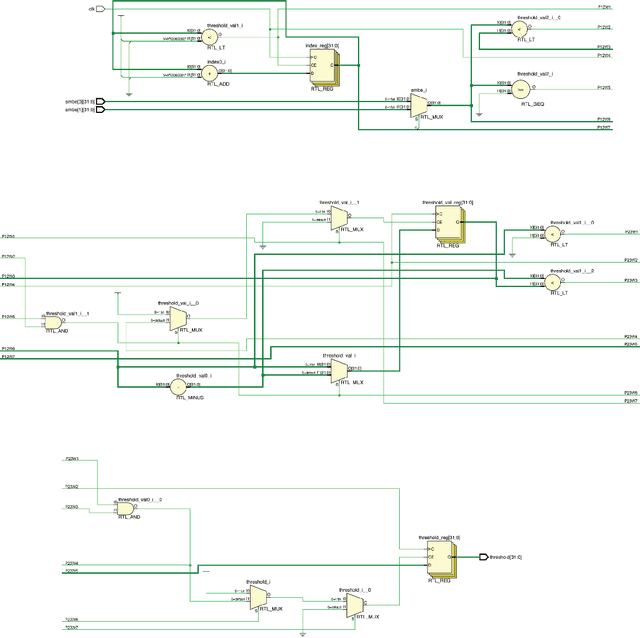
Histogram Equalization (HE) is a popular method for contrast enhancement. Generally, mean brightness is not conserved in Histogram Equalization. Initially, Bi-Histogram Equalization (BBHE) was proposed to enhance contrast while maintaining a the mean brightness. However, when mean brightness is primary concern, Minimum Mean Brightness Error Bi-Histogram Equalization (MMBEBHE) is the best technique. There are several implementations of Histogram Equalization on FPGA, however to our knowledge MMBEBHE has not been implemented on FPGAs before. Therefore, we present an implementation of MMBEBHE on FPGA.