Sparse Views, Near Light: A Practical Paradigm for Uncalibrated Point-light Photometric Stereo

Neural approaches have shown a significant progress on camera-based reconstruction. But they require either a fairly dense sampling of the viewing sphere, or pre-training on an existing dataset, thereby limiting their generalizability. In contrast, photometric stereo (PS) approaches have shown great potential for achieving high-quality reconstruction under sparse viewpoints. Yet, they are impractical because they typically require tedious laboratory conditions, are restricted to dark rooms, and often multi-staged, making them subject to accumulated errors. To address these shortcomings, we propose an end-to-end uncalibrated multi-view PS framework for reconstructing high-resolution shapes acquired from sparse viewpoints in a real-world environment. We relax the dark room assumption, and allow a combination of static ambient lighting and dynamic near LED lighting, thereby enabling easy data capture outside the lab. Experimental validation confirms that it outperforms existing baseline approaches in the regime of sparse viewpoints by a large margin. This allows to bring high-accuracy 3D reconstruction from the dark room to the real world, while maintaining a reasonable data capture complexity.

Enhancing Hypergradients Estimation: A Study of Preconditioning and Reparameterization

Bilevel optimization aims to optimize an outer objective function that depends on the solution to an inner optimization problem. It is routinely used in Machine Learning, notably for hyperparameter tuning. The conventional method to compute the so-called hypergradient of the outer problem is to use the Implicit Function Theorem (IFT). As a function of the error of the inner problem resolution, we study the error of the IFT method. We analyze two strategies to reduce this error: preconditioning the IFT formula and reparameterizing the inner problem. We give a detailed account of the impact of these two modifications on the error, highlighting the role played by higher-order derivatives of the functionals at stake. Our theoretical findings explain when super efficiency, namely reaching an error on the hypergradient that depends quadratically on the error on the inner problem, is achievable and compare the two approaches when this is impossible. Numerical evaluations on hyperparameter tuning for regression problems substantiate our theoretical findings.

Joint Deep Multi-Graph Matching and 3D Geometry Learning from Inhomogeneous 2D Image Collections

Graph matching aims to establish correspondences between vertices of graphs such that both the node and edge attributes agree. Various learning-based methods were recently proposed for finding correspondences between image key points based on deep graph matching formulations. While these approaches mainly focus on learning node and edge attributes, they completely ignore the 3D geometry of the underlying 3D objects depicted in the 2D images. We fill this gap by proposing a trainable framework that takes advantage of graph neural networks for learning a deformable 3D geometry model from inhomogeneous image collections, i.e. a set of images that depict different instances of objects from the same category. Experimentally we demonstrate that our method outperforms recent learning-based approaches for graph matching considering both accuracy and cycle-consistency error, while we in addition obtain the underlying 3D geometry of the objects depicted in the 2D images.

Optimization of Graph Total Variation via Active-Set-based Combinatorial Reconditioning

Structured convex optimization on weighted graphs finds numerous applications in machine learning and computer vision. In this work, we propose a novel adaptive preconditioning strategy for proximal algorithms on this problem class. Our preconditioner is driven by a sharp analysis of the local linear convergence rate depending on the "active set" at the current iterate. We show that nested-forest decomposition of the inactive edges yields a guaranteed local linear convergence rate. Further, we propose a practical greedy heuristic which realizes such nested decompositions and show in several numerical experiments that our reconditioning strategy, when applied to proximal gradient or primal-dual hybrid gradient algorithm, achieves competitive performances. Our results suggest that local convergence analysis can serve as a guideline for selecting variable metrics in proximal algorithms.

Variational Uncalibrated Photometric Stereo under General Lighting

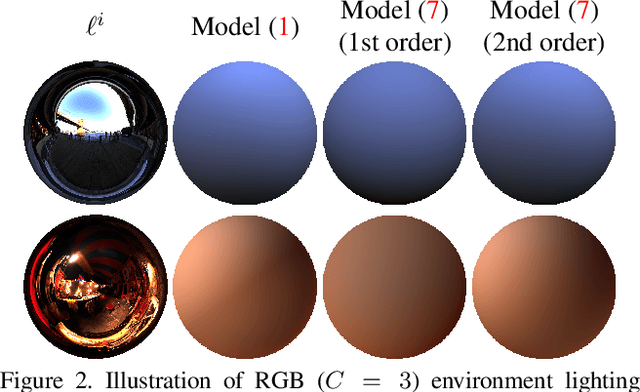
Photometric stereo (PS) techniques nowadays remain constrained to an ideal laboratory setup where modeling and calibration of lighting is amenable. This work aims to eliminate such restrictions. To this end, we introduce an efficient principled variational approach to uncalibrated PS under general illumination, which is approximated through a second-order spherical harmonic expansion. The joint recovery of shape, reflectance and illumination is formulated as a variational problem where shape estimation is carried out directly in terms of the underlying perspective depth map, thus implicitly ensuring integrability and bypassing the need for a subsequent normal integration. We provide a tailored numerical scheme to solve the resulting nonconvex problem efficiently and robustly. On a variety of evaluations, our method consistently reduces the mean angular error by a factor of 2-3 compared to the state-of-the-art.

Combinatorial Preconditioners for Proximal Algorithms on Graphs

We present a novel preconditioning technique for proximal optimization methods that relies on graph algorithms to construct effective preconditioners. Such combinatorial preconditioners arise from partitioning the graph into forests. We prove that certain decompositions lead to a theoretically optimal condition number. We also show how ideal decompositions can be realized using matroid partitioning and propose efficient greedy variants thereof for large-scale problems. Coupled with specialized solvers for the resulting scaled proximal subproblems, the preconditioned algorithm achieves competitive performance in machine learning and vision applications.