Recovery Guarantees of Unsupervised Neural Networks for Inverse Problems trained with Gradient Descent

Advanced machine learning methods, and more prominently neural networks, have become standard to solve inverse problems over the last years. However, the theoretical recovery guarantees of such methods are still scarce and difficult to achieve. Only recently did unsupervised methods such as Deep Image Prior (DIP) get equipped with convergence and recovery guarantees for generic loss functions when trained through gradient flow with an appropriate initialization. In this paper, we extend these results by proving that these guarantees hold true when using gradient descent with an appropriately chosen step-size/learning rate. We also show that the discretization only affects the overparametrization bound for a two-layer DIP network by a constant and thus that the different guarantees found for the gradient flow will hold for gradient descent.

RNb-NeuS: Reflectance and Normal-based Multi-View 3D Reconstruction

This paper introduces a versatile paradigm for integrating multi-view reflectance and normal maps acquired through photometric stereo. Our approach employs a pixel-wise joint re-parameterization of reflectance and normal, considering them as a vector of radiances rendered under simulated, varying illumination. This re-parameterization enables the seamless integration of reflectance and normal maps as input data in neural volume rendering-based 3D reconstruction while preserving a single optimization objective. In contrast, recent multi-view photometric stereo (MVPS) methods depend on multiple, potentially conflicting objectives. Despite its apparent simplicity, our proposed approach outperforms state-of-the-art approaches in MVPS benchmarks across F-score, Chamfer distance, and mean angular error metrics. Notably, it significantly improves the detailed 3D reconstruction of areas with high curvature or low visibility.

Convergence and Recovery Guarantees of Unsupervised Neural Networks for Inverse Problems

Neural networks have become a prominent approach to solve inverse problems in recent years. While a plethora of such methods was developed to solve inverse problems empirically, we are still lacking clear theoretical guarantees for these methods. On the other hand, many works proved convergence to optimal solutions of neural networks in a more general setting using overparametrization as a way to control the Neural Tangent Kernel. In this work we investigate how to bridge these two worlds and we provide deterministic convergence and recovery guarantees for the class of unsupervised feedforward multilayer neural networks trained to solve inverse problems. We also derive overparametrization bounds under which a two-layers Deep Inverse Prior network with smooth activation function will benefit from our guarantees.

Convergence Guarantees of Overparametrized Wide Deep Inverse Prior

Neural networks have become a prominent approach to solve inverse problems in recent years. Amongst the different existing methods, the Deep Image/Inverse Priors (DIPs) technique is an unsupervised approach that optimizes a highly overparametrized neural network to transform a random input into an object whose image under the forward model matches the observation. However, the level of overparametrization necessary for such methods remains an open problem. In this work, we aim to investigate this question for a two-layers neural network with a smooth activation function. We provide overparametrization bounds under which such network trained via continuous-time gradient descent will converge exponentially fast with high probability which allows to derive recovery prediction bounds. This work is thus a first step towards a theoretical understanding of overparametrized DIP networks, and more broadly it participates to the theoretical understanding of neural networks in inverse problem settings.

MS-PS: A Multi-Scale Network for Photometric Stereo With a New Comprehensive Training Dataset

The photometric stereo (PS) problem consists in reconstructing the 3D-surface of an object, thanks to a set of photographs taken under different lighting directions. In this paper, we propose a multi-scale architecture for PS which, combined with a new dataset, yields state-of-the-art results. Our proposed architecture is flexible: it permits to consider a variable number of images as well as variable image size without loss of performance. In addition, we define a set of constraints to allow the generation of a relevant synthetic dataset to train convolutional neural networks for the PS problem. Our proposed dataset is much larger than pre-existing ones, and contains many objects with challenging materials having anisotropic reflectance (e.g. metals, glass). We show on publicly available benchmarks that the combination of both these contributions drastically improves the accuracy of the estimated normal field, in comparison with previous state-of-the-art methods.

On the well-posedness of uncalibrated photometric stereo under general lighting

Uncalibrated photometric stereo aims at estimating the 3D-shape of a surface, given a set of images captured from the same viewing angle, but under unknown, varying illumination. While the theoretical foundations of this inverse problem under directional lighting are well-established, there is a lack of mathematical evidence for the uniqueness of a solution under general lighting. On the other hand, stable and accurate heuristical solutions of uncalibrated photometric stereo under such general lighting have recently been proposed. The quality of the results demonstrated therein tends to indicate that the problem may actually be well-posed, but this still has to be established. The present paper addresses this theoretical issue, considering first-order spherical harmonics approximation of general lighting. Two important theoretical results are established. First, the orthographic integrability constraint ensures uniqueness of a solution up to a global concave-convex ambiguity, which had already been conjectured, yet not proven. Second, the perspective integrability constraint makes the problem well-posed, which generalizes a previous result limited to directional lighting. Eventually, a closed-form expression for the unique least-squares solution of the problem under perspective projection is provided, allowing numerical simulations on synthetic data to empirically validate our findings.

Variational Uncalibrated Photometric Stereo under General Lighting

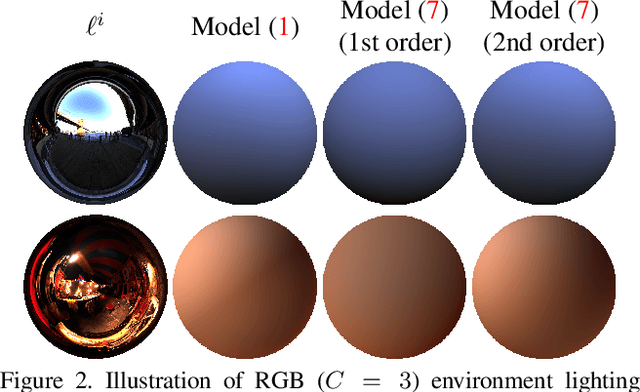
Photometric stereo (PS) techniques nowadays remain constrained to an ideal laboratory setup where modeling and calibration of lighting is amenable. This work aims to eliminate such restrictions. To this end, we introduce an efficient principled variational approach to uncalibrated PS under general illumination, which is approximated through a second-order spherical harmonic expansion. The joint recovery of shape, reflectance and illumination is formulated as a variational problem where shape estimation is carried out directly in terms of the underlying perspective depth map, thus implicitly ensuring integrability and bypassing the need for a subsequent normal integration. We provide a tailored numerical scheme to solve the resulting nonconvex problem efficiently and robustly. On a variety of evaluations, our method consistently reduces the mean angular error by a factor of 2-3 compared to the state-of-the-art.

Photometric Depth Super-Resolution

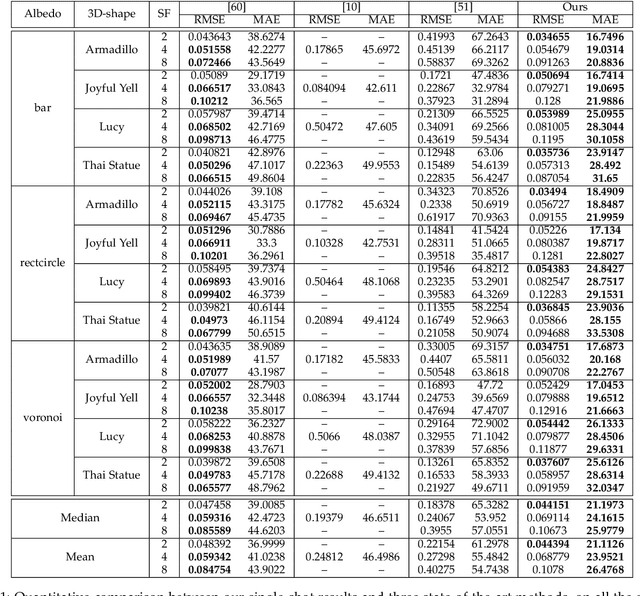
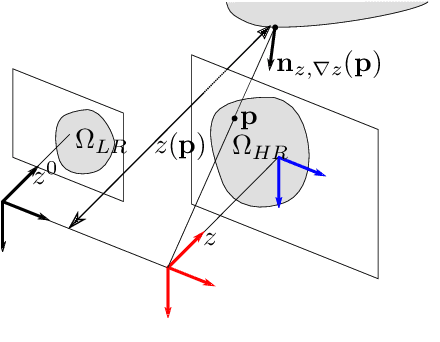
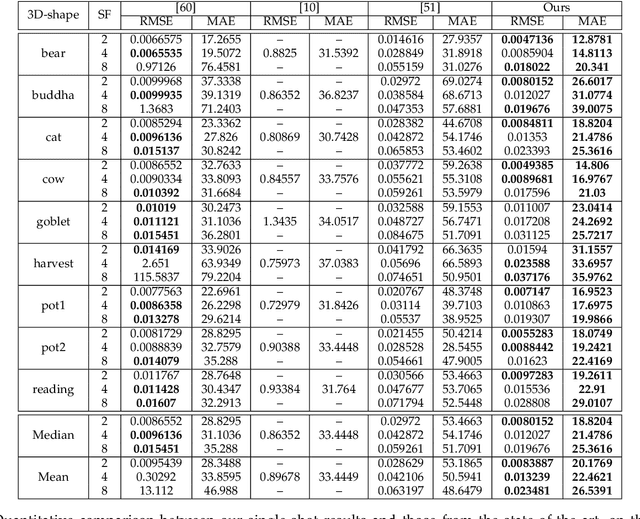
This study explores the use of photometric techniques (shape-from-shading and uncalibrated photometric stereo) for upsampling the low-resolution depth map from an RGB-D sensor to the higher resolution of the companion RGB image. A single-shot variational approach is first put forward, which is effective as long as the target's reflectance is piecewise-constant. It is then shown that this dependency upon a specific reflectance model can be relaxed by focusing on a specific class of objects (e.g., faces), and delegate reflectance estimation to a deep neural network. A multi-shots strategy based on randomly varying lighting conditions is eventually discussed. It requires no training or prior on the reflectance, yet this comes at the price of a dedicated acquisition setup. Both quantitative and qualitative evaluations illustrate the effectiveness of the proposed methods on synthetic and real-world scenarios.

Variational Reflectance Estimation from Multi-view Images

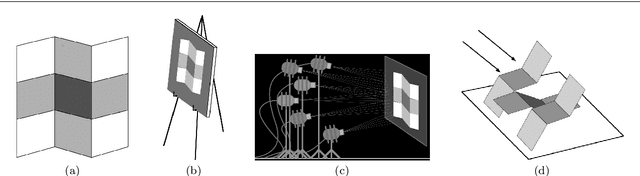
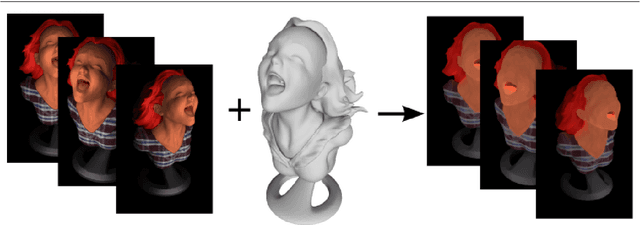
We tackle the problem of reflectance estimation from a set of multi-view images, assuming known geometry. The approach we put forward turns the input images into reflectance maps, through a robust variational method. The variational model comprises an image-driven fidelity term and a term which enforces consistency of the reflectance estimates with respect to each view. If illumination is fixed across the views, then reflectance estimation remains under-constrained: a regularization term, which ensures piecewise-smoothness of the reflectance, is thus used. Reflectance is parameterized in the image domain, rather than on the surface, which makes the numerical solution much easier, by resorting to an alternating majorization-minimization approach. Experiments on both synthetic and real datasets are carried out to validate the proposed strategy.

A Variational Approach to Shape-from-shading Under Natural Illumination

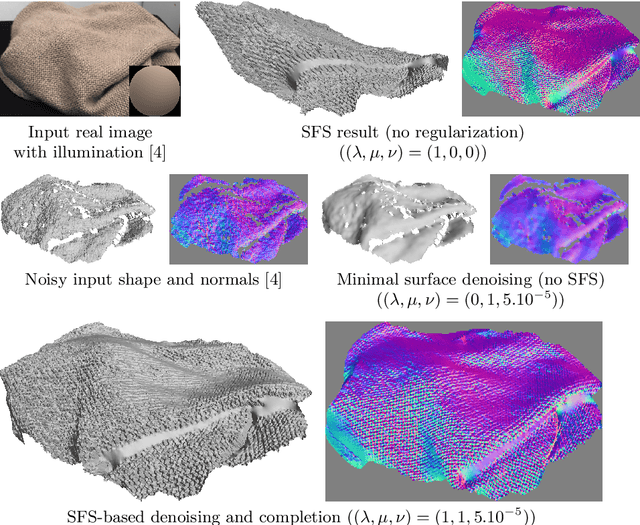
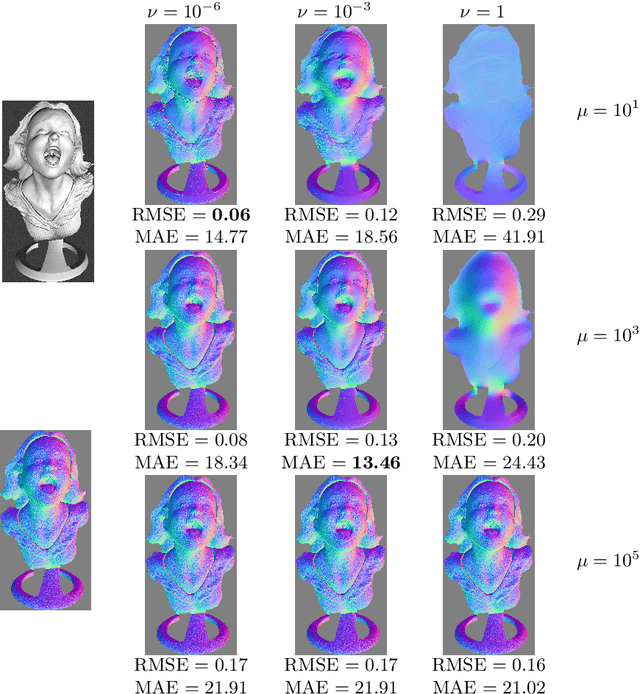
A numerical solution to shape-from-shading under natural illumination is presented. It builds upon an augmented Lagrangian approach for solving a generic PDE-based shape-from-shading model which handles directional or spherical harmonic lighting, orthographic or perspective projection, and greylevel or multi-channel images. Real-world applications to shading-aware depth map denoising, refinement and completion are presented.