Jean-Denis Durou
IRIT-REVA, Toulouse INP
Light and 3D: a methodological exploration of digitisation techniques adapted to a selection of objects from the Mus{é}e d'Arch{é}ologie Nationale
Jun 05, 2025Abstract:The need to digitize heritage objects is now widely accepted. This article presents the very fashionable context of the creation of ''digital twins''. It illustrates the diversity of photographic 3D digitization methods, but this is not its only objective. Using a selection of objects from the collections of the mus{\'e}e d'Arch{\'e}ologie nationale, it shows that no single method is suitable for all cases. Rather, the method to be recommended for a given object should be the result of a concerted choice between those involved in heritage and those involved in the digital domain, as each new object may require the adaptation of existing tools. It would therefore be pointless to attempt an absolute classification of 3D digitization methods. On the contrary, we need to find the digital tool best suited to each object, taking into account not only its characteristics, but also the future use of its digital twin.
* in French language
Multi-view Surface Reconstruction Using Normal and Reflectance Cues
Jun 04, 2025Abstract:Achieving high-fidelity 3D surface reconstruction while preserving fine details remains challenging, especially in the presence of materials with complex reflectance properties and without a dense-view setup. In this paper, we introduce a versatile framework that incorporates multi-view normal and optionally reflectance maps into radiance-based surface reconstruction. Our approach employs a pixel-wise joint re-parametrization of reflectance and surface normals, representing them as a vector of radiances under simulated, varying illumination. This formulation enables seamless incorporation into standard surface reconstruction pipelines, such as traditional multi-view stereo (MVS) frameworks or modern neural volume rendering (NVR) ones. Combined with the latter, our approach achieves state-of-the-art performance on multi-view photometric stereo (MVPS) benchmark datasets, including DiLiGenT-MV, LUCES-MV and Skoltech3D. In particular, our method excels in reconstructing fine-grained details and handling challenging visibility conditions. The present paper is an extended version of the earlier conference paper by Brument et al. (in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2024), featuring an accelerated and more robust algorithm as well as a broader empirical evaluation. The code and data relative to this article is available at https://github.com/RobinBruneau/RNb-NeuS2.
RNb-NeuS: Reflectance and Normal-based Multi-View 3D Reconstruction
Dec 02, 2023Abstract:This paper introduces a versatile paradigm for integrating multi-view reflectance and normal maps acquired through photometric stereo. Our approach employs a pixel-wise joint re-parameterization of reflectance and normal, considering them as a vector of radiances rendered under simulated, varying illumination. This re-parameterization enables the seamless integration of reflectance and normal maps as input data in neural volume rendering-based 3D reconstruction while preserving a single optimization objective. In contrast, recent multi-view photometric stereo (MVPS) methods depend on multiple, potentially conflicting objectives. Despite its apparent simplicity, our proposed approach outperforms state-of-the-art approaches in MVPS benchmarks across F-score, Chamfer distance, and mean angular error metrics. Notably, it significantly improves the detailed 3D reconstruction of areas with high curvature or low visibility.
Variational Reflectance Estimation from Multi-view Images
Jan 23, 2018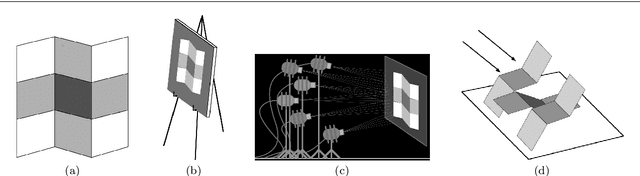

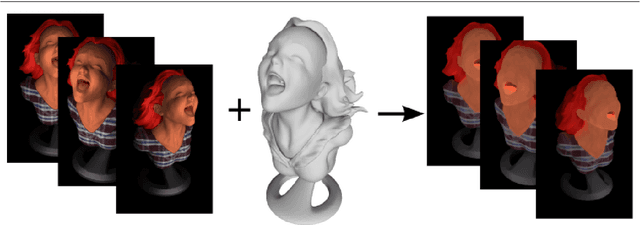
Abstract:We tackle the problem of reflectance estimation from a set of multi-view images, assuming known geometry. The approach we put forward turns the input images into reflectance maps, through a robust variational method. The variational model comprises an image-driven fidelity term and a term which enforces consistency of the reflectance estimates with respect to each view. If illumination is fixed across the views, then reflectance estimation remains under-constrained: a regularization term, which ensures piecewise-smoothness of the reflectance, is thus used. Reflectance is parameterized in the image domain, rather than on the surface, which makes the numerical solution much easier, by resorting to an alternating majorization-minimization approach. Experiments on both synthetic and real datasets are carried out to validate the proposed strategy.
A Variational Approach to Shape-from-shading Under Natural Illumination
Dec 03, 2017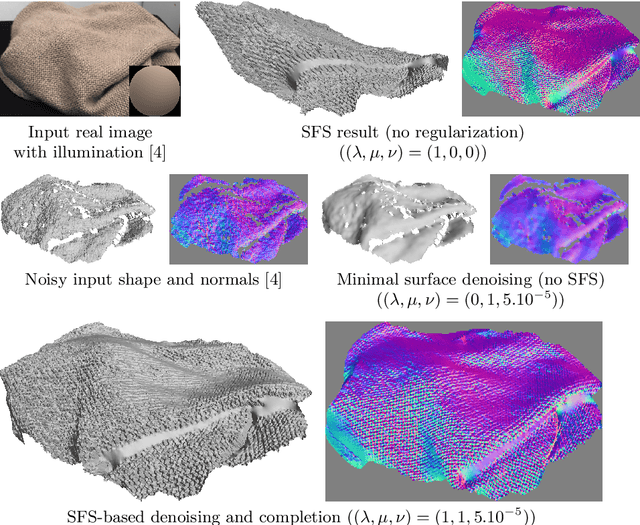


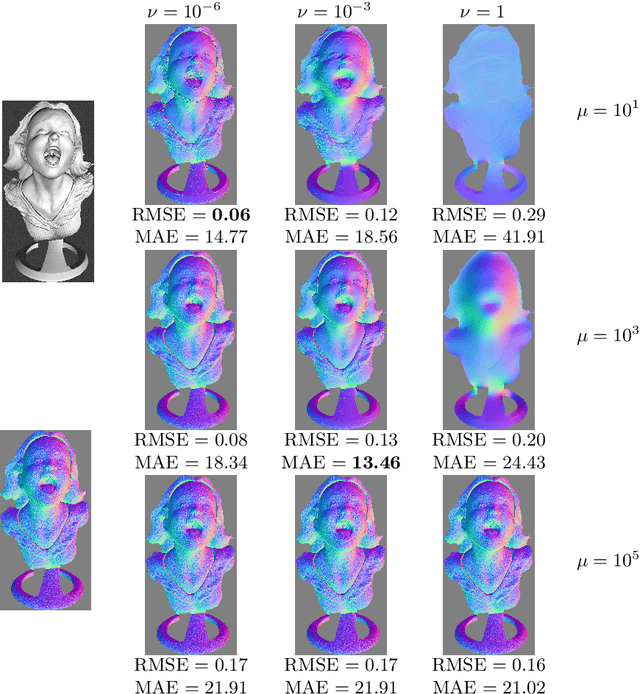
Abstract:A numerical solution to shape-from-shading under natural illumination is presented. It builds upon an augmented Lagrangian approach for solving a generic PDE-based shape-from-shading model which handles directional or spherical harmonic lighting, orthographic or perspective projection, and greylevel or multi-channel images. Real-world applications to shading-aware depth map denoising, refinement and completion are presented.
Variational Methods for Normal Integration
Sep 18, 2017

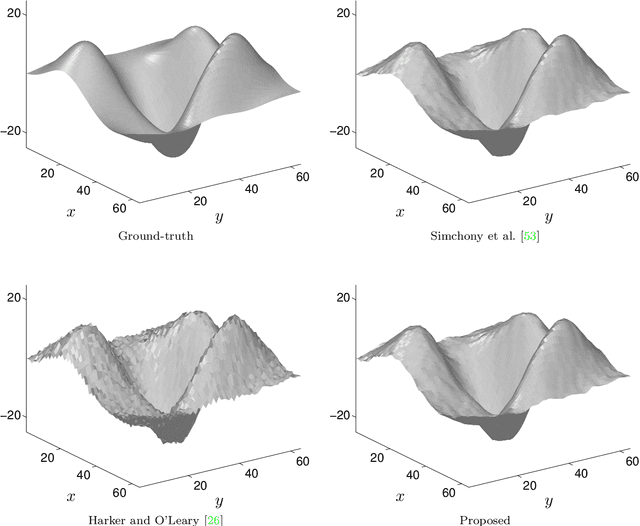
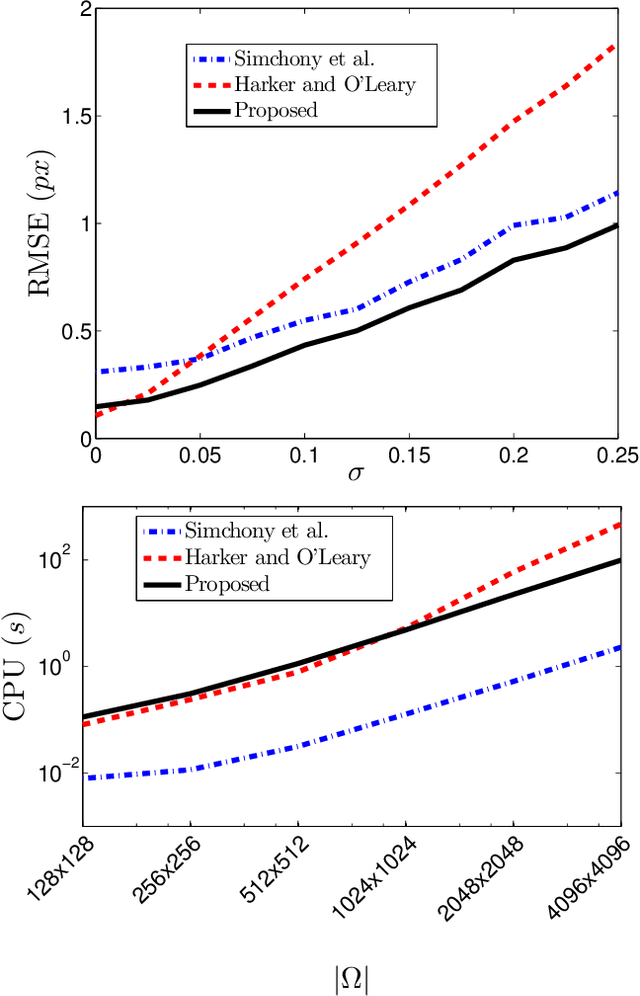
Abstract:The need for an efficient method of integration of a dense normal field is inspired by several computer vision tasks, such as shape-from-shading, photometric stereo, deflectometry, etc. Inspired by edge-preserving methods from image processing, we study in this paper several variational approaches for normal integration, with a focus on non-rectangular domains, free boundary and depth discontinuities. We first introduce a new discretization for quadratic integration, which is designed to ensure both fast recovery and the ability to handle non-rectangular domains with a free boundary. Yet, with this solver, discontinuous surfaces can be handled only if the scene is first segmented into pieces without discontinuity. Hence, we then discuss several discontinuity-preserving strategies. Those inspired, respectively, by the Mumford-Shah segmentation method and by anisotropic diffusion, are shown to be the most effective for recovering discontinuities.
Normal Integration: A Survey
Sep 18, 2017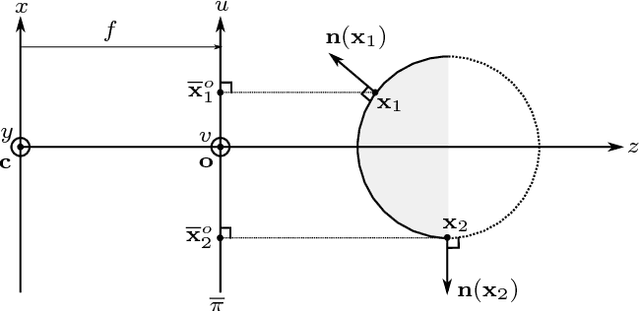
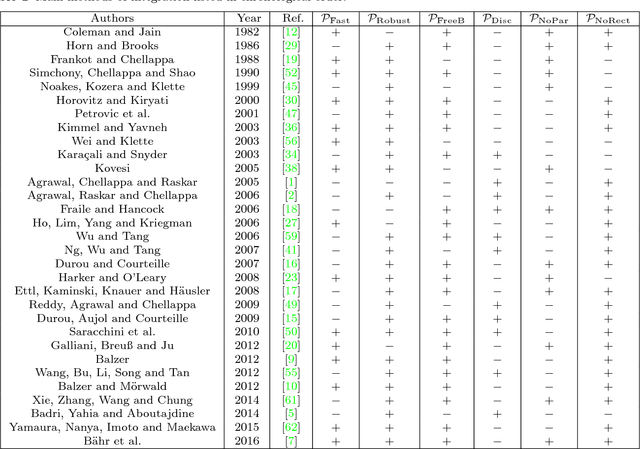

Abstract:The need for efficient normal integration methods is driven by several computer vision tasks such as shape-from-shading, photometric stereo, deflectometry, etc. In the first part of this survey, we select the most important properties that one may expect from a normal integration method, based on a thorough study of two pioneering works by Horn and Brooks [28] and by Frankot and Chellappa [19]. Apart from accuracy, an integration method should at least be fast and robust to a noisy normal field. In addition, it should be able to handle several types of boundary condition, including the case of a free boundary, and a reconstruction domain of any shape i.e., which is not necessarily rectangular. It is also much appreciated that a minimum number of parameters have to be tuned, or even no parameter at all. Finally, it should preserve the depth discontinuities. In the second part of this survey, we review most of the existing methods in view of this analysis, and conclude that none of them satisfies all of the required properties. This work is complemented by a companion paper entitled Variational Methods for Normal Integration, in which we focus on the problem of normal integration in the presence of depth discontinuities, a problem which occurs as soon as there are occlusions.
LED-based Photometric Stereo: Modeling, Calibration and Numerical Solution
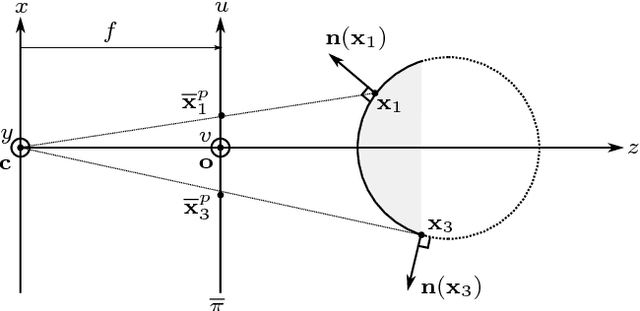
Sep 04, 2017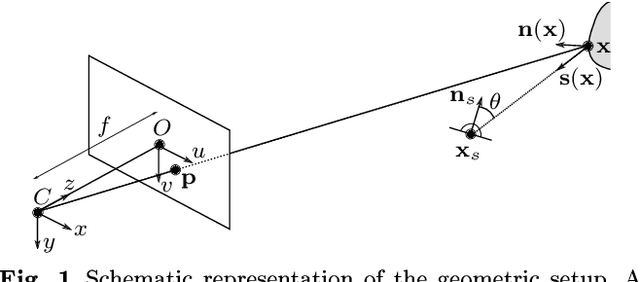


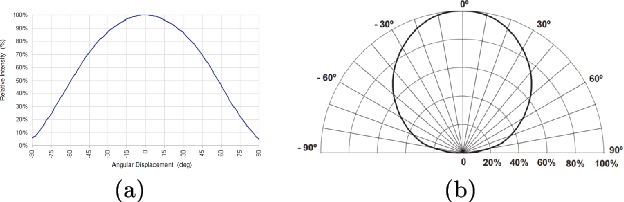
Abstract:We conduct a thorough study of photometric stereo under nearby point light source illumination, from modeling to numerical solution, through calibration. In the classical formulation of photometric stereo, the luminous fluxes are assumed to be directional, which is very difficult to achieve in practice. Rather, we use light-emitting diodes (LEDs) to illuminate the scene to reconstruct. Such point light sources are very convenient to use, yet they yield a more complex photometric stereo model which is arduous to solve. We first derive in a physically sound manner this model, and show how to calibrate its parameters. Then, we discuss two state-of-the-art numerical solutions. The first one alternatingly estimates the albedo and the normals, and then integrates the normals into a depth map. It is shown empirically to be independent from the initialization, but convergence of this sequential approach is not established. The second one directly recovers the depth, by formulating photometric stereo as a system of PDEs which are partially linearized using image ratios. Although the sequential approach is avoided, initialization matters a lot and convergence is not established either. Therefore, we introduce a provably convergent alternating reweighted least-squares scheme for solving the original system of PDEs, without resorting to image ratios for linearization. Finally, we extend this study to the case of RGB images.
Dense Multi-view 3D-reconstruction Without Dense Correspondences
Apr 02, 2017
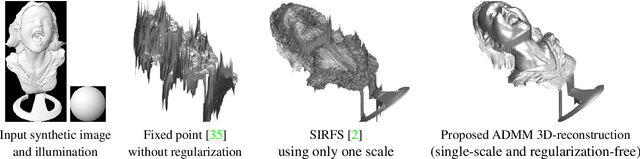


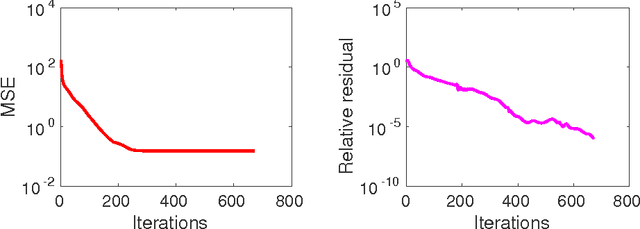
Abstract:We introduce a variational method for multi-view shape-from-shading under natural illumination. The key idea is to couple PDE-based solutions for single-image based shape-from-shading problems across multiple images and multiple color channels by means of a variational formulation. Rather than alternatingly solving the individual SFS problems and optimizing the consistency across images and channels which is known to lead to suboptimal results, we propose an efficient solution of the coupled problem by means of an ADMM algorithm. In numerous experiments on both simulated and real imagery, we demonstrate that the proposed fusion of multiple-view reconstruction and shape-from-shading provides highly accurate dense reconstructions without the need to compute dense correspondences. With the proposed variational integration across multiple views shape-from-shading techniques become applicable to challenging real-world reconstruction problems, giving rise to highly detailed geometry even in areas of smooth brightness variation and lacking texture.
Fast and Accurate Surface Normal Integration on Non-Rectangular Domains
Oct 19, 2016


Abstract:The integration of surface normals for the purpose of computing the shape of a surface in 3D space is a classic problem in computer vision. However, even nowadays it is still a challenging task to devise a method that combines the flexibility to work on non-trivial computational domains with high accuracy, robustness and computational efficiency. By uniting a classic approach for surface normal integration with modern computational techniques we construct a solver that fulfils these requirements. Building upon the Poisson integration model we propose to use an iterative Krylov subspace solver as a core step in tackling the task. While such a method can be very efficient, it may only show its full potential when combined with a suitable numerical preconditioning and a problem-specific initialisation. We perform a thorough numerical study in order to identify an appropriate preconditioner for our purpose. To address the issue of a suitable initialisation we propose to compute this initial state via a recently developed fast marching integrator. Detailed numerical experiments illuminate the benefits of this novel combination. In addition, we show on real-world photometric stereo datasets that the developed numerical framework is flexible enough to tackle modern computer vision applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge