Locally orderless networks

We present Locally Orderless Networks (LON) and its theoretic foundation which links it to Convolutional Neural Networks (CNN), to Scale-space histograms, and measurement theory. The key elements are a regular sampling of the bias and the derivative of the activation function. We compare LON, CNN, and Scale-space histograms on prototypical single-layer networks. We show how LON and CNN can emulate each other, how LON expands the set of functionals computable to non-linear functions such as squaring. We demonstrate simple networks which illustrate the improved performance of LON over CNN on simple tasks for estimating the gradient magnitude squared, for regressing shape area and perimeter lengths, and for explainability of individual pixels' influence on the result.

Information-Theoretic Registration with Explicit Reorientation of Diffusion-Weighted Images

We present an information-theoretic approach to registration of DWI with explicit optimization over the orientational scale, with an additional focus on normalized mutual information as a robust information-theoretic similarity measure for DWI. The framework is an extension of the LOR-DWI density-based hierarchical scale-space model, that varies and optimizes over the integration, spatial, directional, and intensity scales. We extend the model to non-rigid deformations and show that the formulation provides intrinsic regularization through the orientational information. Our experiments illustrate that the proposed model deforms ODFs correctly and is capable of handling the classic complex challenges in DWI-registrations, such as the registration of fiber-crossings along with kissing, fanning and interleaving fibers. Our results clearly illustrate a novel promising regularizing effect, that comes from the nonlinear orientation-based cost function. We illustrate the properties of the different image scales, and show that including orientational information in our model make the model better at retrieving deformations compared to standard scalar-based registration.

LED-based Photometric Stereo: Modeling, Calibration and Numerical Solution

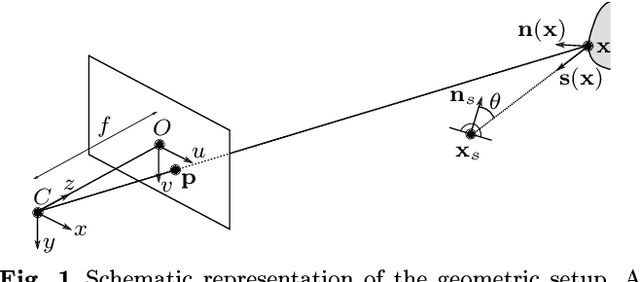
We conduct a thorough study of photometric stereo under nearby point light source illumination, from modeling to numerical solution, through calibration. In the classical formulation of photometric stereo, the luminous fluxes are assumed to be directional, which is very difficult to achieve in practice. Rather, we use light-emitting diodes (LEDs) to illuminate the scene to reconstruct. Such point light sources are very convenient to use, yet they yield a more complex photometric stereo model which is arduous to solve. We first derive in a physically sound manner this model, and show how to calibrate its parameters. Then, we discuss two state-of-the-art numerical solutions. The first one alternatingly estimates the albedo and the normals, and then integrates the normals into a depth map. It is shown empirically to be independent from the initialization, but convergence of this sequential approach is not established. The second one directly recovers the depth, by formulating photometric stereo as a system of PDEs which are partially linearized using image ratios. Although the sequential approach is avoided, initialization matters a lot and convergence is not established either. Therefore, we introduce a provably convergent alternating reweighted least-squares scheme for solving the original system of PDEs, without resorting to image ratios for linearization. Finally, we extend this study to the case of RGB images.

Scale-Regularized Filter Learning

We start out by demonstrating that an elementary learning task, corresponding to the training of a single linear neuron in a convolutional neural network, can be solved for feature spaces of very high dimensionality. In a second step, acknowledging that such high-dimensional learning tasks typically benefit from some form of regularization and arguing that the problem of scale has not been taken care of in a very satisfactory manner, we come to a combined resolution of both of these shortcomings by proposing a form of scale regularization. Moreover, using variational method, this regularization problem can also be solved rather efficiently and we demonstrate, on an artificial filter learning problem, the capabilities of our basic linear neuron. From a more general standpoint, we see this work as prime example of how learning and variational methods could, or even should work to their mutual benefit.