Inductive Conformal Prediction under Data Scarcity: Exploring the Impacts of Nonconformity Measures

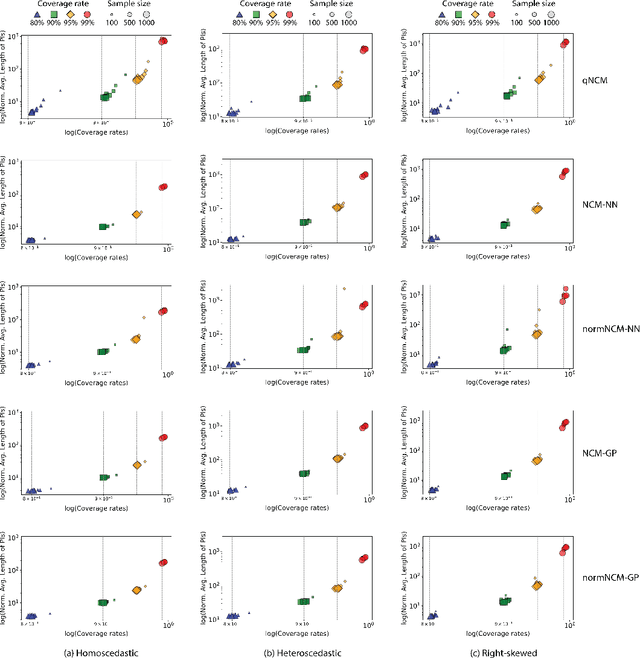
Conformal prediction, which makes no distributional assumptions about the data, has emerged as a powerful and reliable approach to uncertainty quantification in practical applications. The nonconformity measure used in conformal prediction quantifies how a test sample differs from the training data and the effectiveness of a conformal prediction interval may depend heavily on the precise measure employed. The impact of this choice has, however, not been widely explored, especially when dealing with limited amounts of data. The primary objective of this study is to evaluate the performance of various nonconformity measures (absolute error-based, normalized absolute error-based, and quantile-based measures) in terms of validity and efficiency when used in inductive conformal prediction. The focus is on small datasets, which is still a common setting in many real-world applications. Using synthetic and real-world data, we assess how different characteristics -- such as dataset size, noise, and dimensionality -- can affect the efficiency of conformal prediction intervals. Our results show that although there are differences, no single nonconformity measure consistently outperforms the others, as the effectiveness of each nonconformity measure is heavily influenced by the specific nature of the data. Additionally, we found that increasing dataset size does not always improve efficiency, suggesting the importance of fine-tuning models and, again, the need to carefully select the nonconformity measure for different applications.

A Survey of Learning Curves with Bad Behavior: or How More Data Need Not Lead to Better Performance

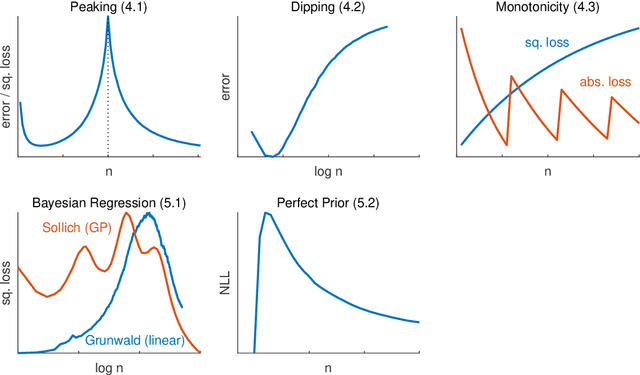
Plotting a learner's generalization performance against the training set size results in a so-called learning curve. This tool, providing insight in the behavior of the learner, is also practically valuable for model selection, predicting the effect of more training data, and reducing the computational complexity of training. We set out to make the (ideal) learning curve concept precise and briefly discuss the aforementioned usages of such curves. The larger part of this survey's focus, however, is on learning curves that show that more data does not necessarily leads to better generalization performance. A result that seems surprising to many researchers in the field of artificial intelligence. We point out the significance of these findings and conclude our survey with an overview and discussion of open problems in this area that warrant further theoretical and empirical investigation.

A view on model misspecification in uncertainty quantification

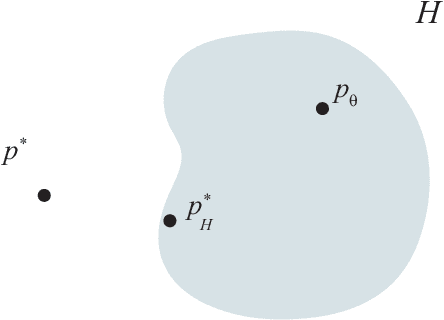
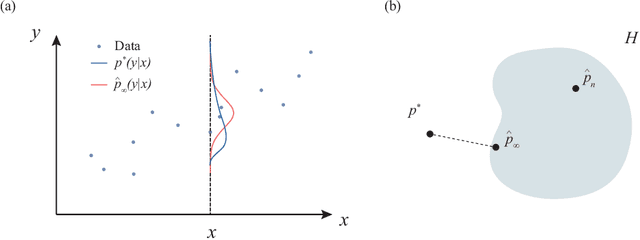
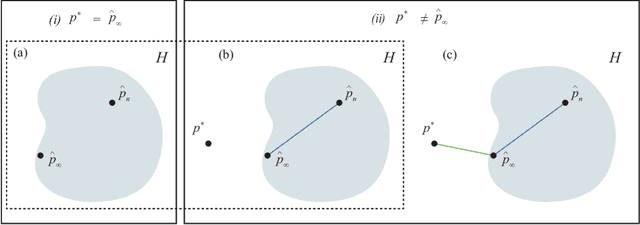
Estimating uncertainty of machine learning models is essential to assess the quality of the predictions that these models provide. However, there are several factors that influence the quality of uncertainty estimates, one of which is the amount of model misspecification. Model misspecification always exists as models are mere simplifications or approximations to reality. The question arises whether the estimated uncertainty under model misspecification is reliable or not. In this paper, we argue that model misspecification should receive more attention, by providing thought experiments and contextualizing these with relevant literature.

An Analysis of Abstracted Model-Based Reinforcement Learning

Many methods for Model-based Reinforcement learning (MBRL) provide guarantees for both the accuracy of the Markov decision process (MDP) model they can deliver and the learning efficiency. At the same time, state abstraction techniques allow for a reduction of the size of an MDP while maintaining a bounded loss with respect to the original problem. It may come as a surprise, therefore, that no such guarantees are available when combining both techniques, i.e., where MBRL merely observes abstract states. Our theoretical analysis shows that abstraction can introduce a dependence between samples collected online (e.g., in the real world), which means that most results for MBRL can not be directly extended to this setting. The new results in this work show that concentration inequalities for martingales can be used to overcome this problem and allows for extending the results of algorithms such as R-MAX to the setting with abstraction. Thus producing the first performance guarantees for Abstracted RL: model-based reinforcement learning with an abstracted model.

On the reusability of samples in active learning

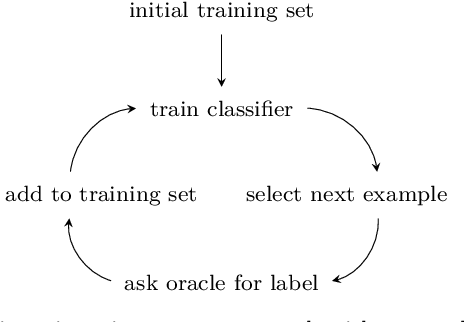
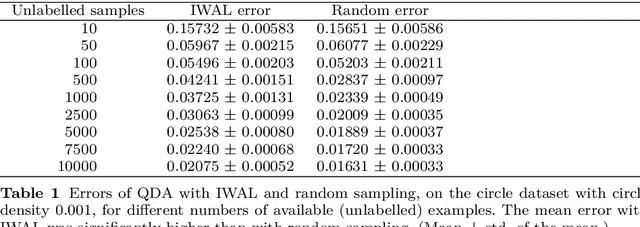
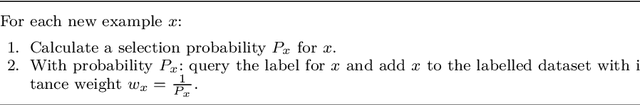
An interesting but not extensively studied question in active learning is that of sample reusability: to what extent can samples selected for one learner be reused by another? This paper explains why sample reusability is of practical interest, why reusability can be a problem, how reusability could be improved by importance-weighted active learning, and which obstacles to universal reusability remain. With theoretical arguments and practical demonstrations, this paper argues that universal reusability is impossible. Because every active learning strategy must undersample some areas of the sample space, learners that depend on the samples in those areas will learn more from a random sample selection. This paper describes several experiments with importance-weighted active learning that show the impact of the reusability problem in practice. The experiments confirmed that universal reusability does not exist, although in some cases -- on some datasets and with some pairs of classifiers -- there is sample reusability. Finally, this paper explores the conditions that could guarantee the reusability between two classifiers.

Why Did This Model Forecast This Future? Closed-Form Temporal Saliency Towards Causal Explanations of Probabilistic Forecasts

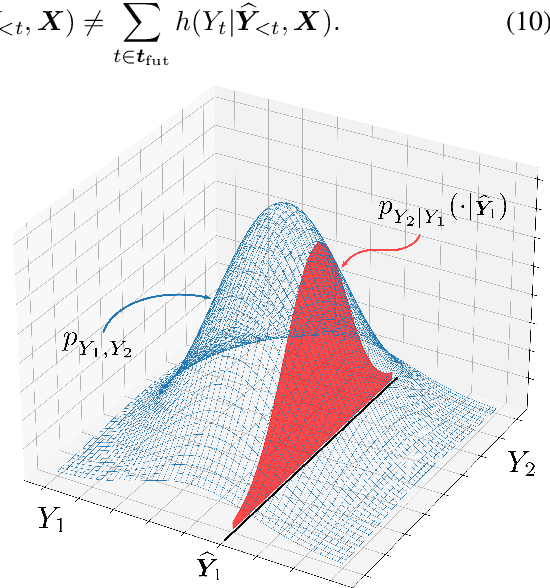
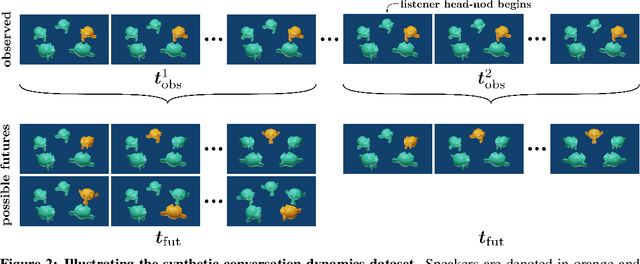
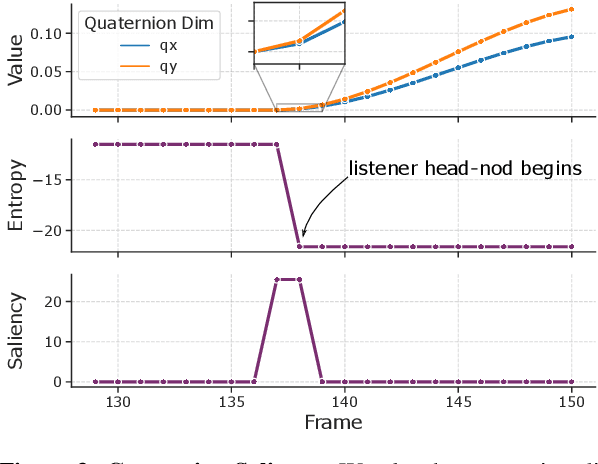
Forecasting tasks surrounding the dynamics of low-level human behavior are of significance to multiple research domains. In such settings, methods for explaining specific forecasts can enable domain experts to gain insights into the predictive relationships between behaviors. In this work, we introduce and address the following question: given a probabilistic forecasting model how can we identify observed windows that the model considers salient when making its forecasts? We build upon a general definition of information-theoretic saliency grounded in human perception and extend it to forecasting settings by leveraging a crucial attribute of the domain: a single observation can result in multiple valid futures. We propose to express the saliency of an observed window in terms of the differential entropy of the resulting predicted future distribution. In contrast to existing methods that either require explicit training of the saliency mechanism or access to the internal states of the forecasting model, we obtain a closed-form solution for the saliency map for commonly used density functions in probabilistic forecasting. We empirically demonstrate how our framework can recover salient observed windows from head pose features for the sample task of speaking-turn forecasting using a synthesized conversation dataset.

Enhancing Classifier Conservativeness and Robustness by Polynomiality

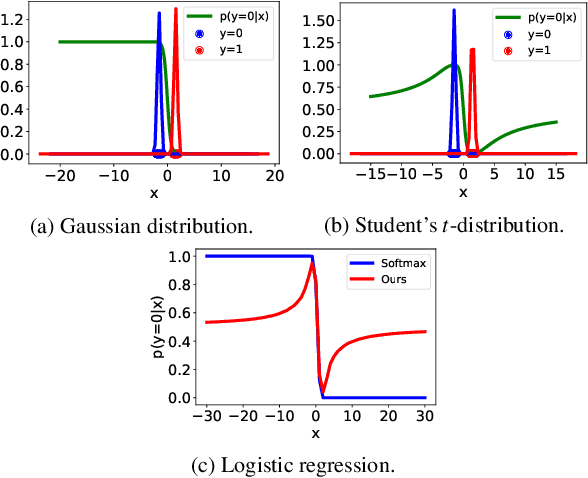
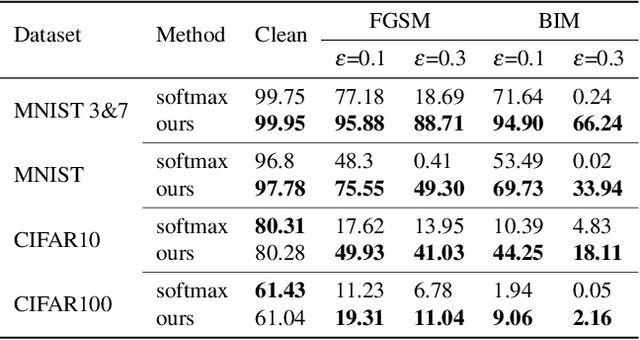
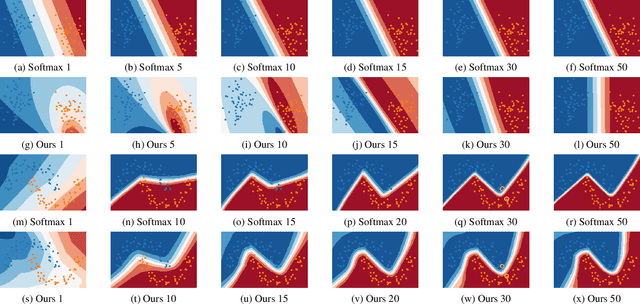
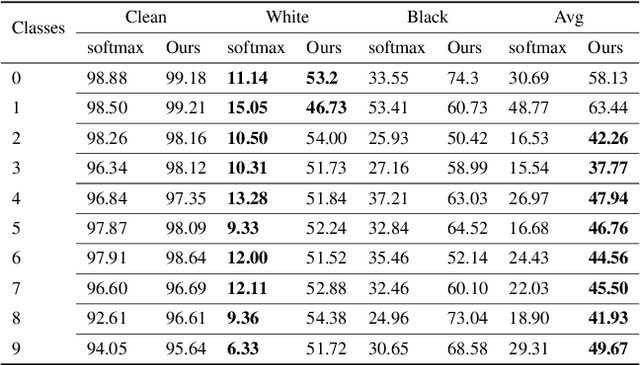
We illustrate the detrimental effect, such as overconfident decisions, that exponential behavior can have in methods like classical LDA and logistic regression. We then show how polynomiality can remedy the situation. This, among others, leads purposefully to random-level performance in the tails, away from the bulk of the training data. A directly related, simple, yet important technical novelty we subsequently present is softRmax: a reasoned alternative to the standard softmax function employed in contemporary (deep) neural networks. It is derived through linking the standard softmax to Gaussian class-conditional models, as employed in LDA, and replacing those by a polynomial alternative. We show that two aspects of softRmax, conservativeness and inherent gradient regularization, lead to robustness against adversarial attacks without gradient obfuscation.

Social Processes: Self-Supervised Forecasting of Nonverbal Cues in Social Conversations

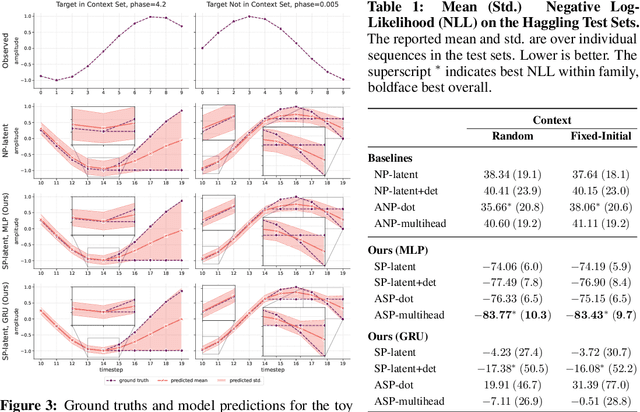
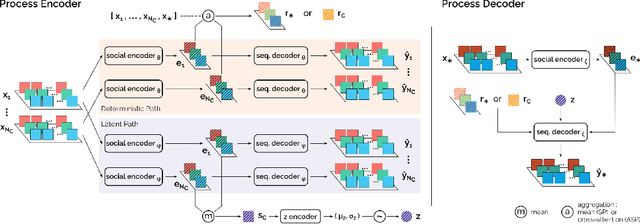
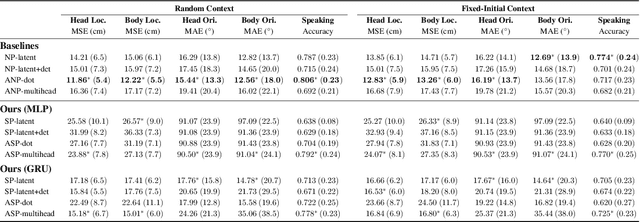
The default paradigm for the forecasting of human behavior in social conversations is characterized by top-down approaches. These involve identifying predictive relationships between low level nonverbal cues and future semantic events of interest (e.g. turn changes, group leaving). A common hurdle however, is the limited availability of labeled data for supervised learning. In this work, we take the first step in the direction of a bottom-up self-supervised approach in the domain. We formulate the task of Social Cue Forecasting to leverage the larger amount of unlabeled low-level behavior cues, and characterize the modeling challenges involved. To address these, we take a meta-learning approach and propose the Social Process (SP) models--socially aware sequence-to-sequence (Seq2Seq) models within the Neural Process (NP) family. SP models learn extractable representations of non-semantic future cues for each participant, while capturing global uncertainty by jointly reasoning about the future for all members of the group. Evaluation on synthesized and real-world behavior data shows that our SP models achieve higher log-likelihood than the NP baselines, and also highlights important considerations for applying such techniques within the domain of social human interactions.

Resolution learning in deep convolutional networks using scale-space theory

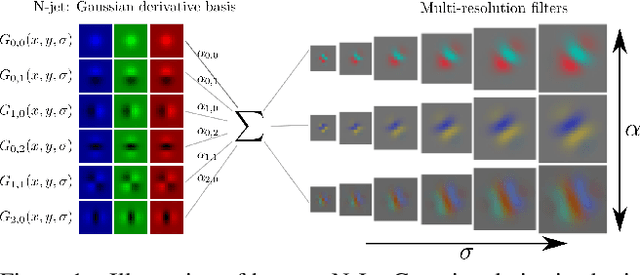
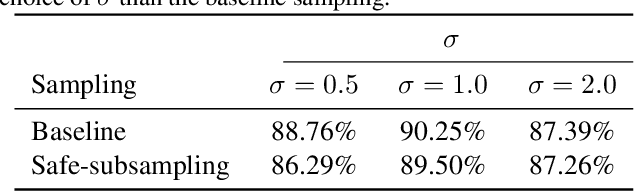
Resolution in deep convolutional neural networks (CNNs) is typically bounded by the receptive field size through filter sizes, and subsampling layers or strided convolutions on feature maps. The optimal resolution may vary significantly depending on the dataset. Modern CNNs hard-code their resolution hyper-parameters in the network architecture which makes tuning such hyper-parameters cumbersome. We propose to do away with hard-coded resolution hyper-parameters and aim to learn the appropriate resolution from data. We use scale-space theory to obtain a self-similar parametrization of filters and make use of the N-Jet: a truncated Taylor series to approximate a filter by a learned combination of Gaussian derivative filters. The parameter sigma of the Gaussian basis controls both the amount of detail the filter encodes and the spatial extent of the filter. Since sigma is a continuous parameter, we can optimize it with respect to the loss. The proposed N-Jet layer achieves comparable performance when used in state-of-the art architectures, while learning the correct resolution in each layer automatically. We evaluate our N-Jet layer on both classification and segmentation, and we show that learning sigma is especially beneficial for inputs at multiple sizes.

The Shape of Learning Curves: a Review

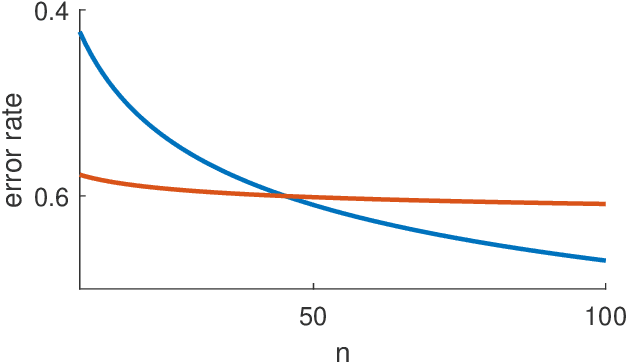
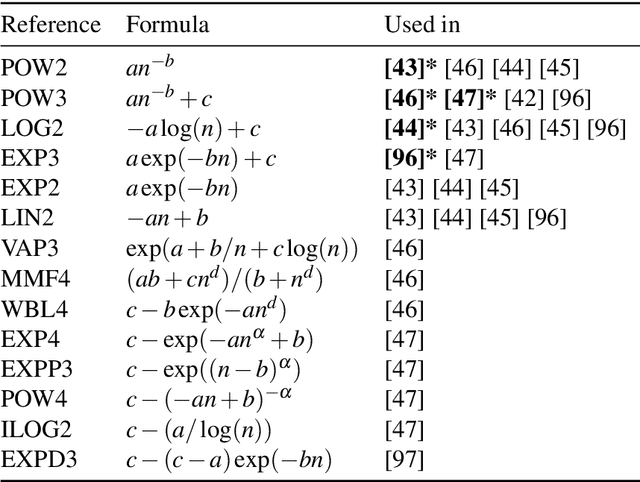
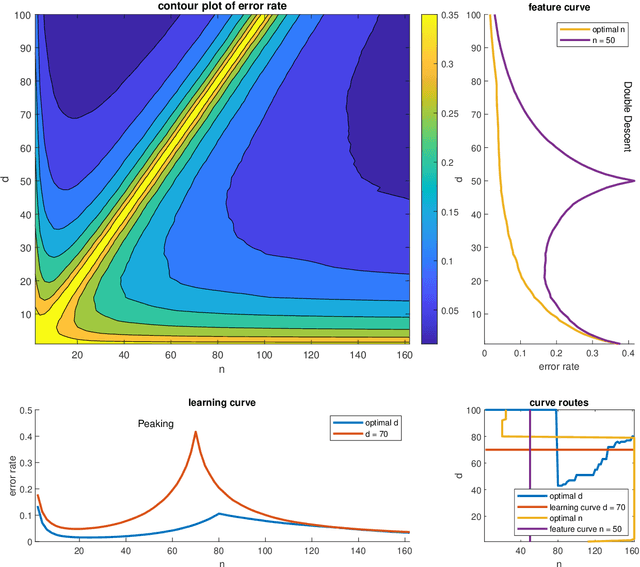
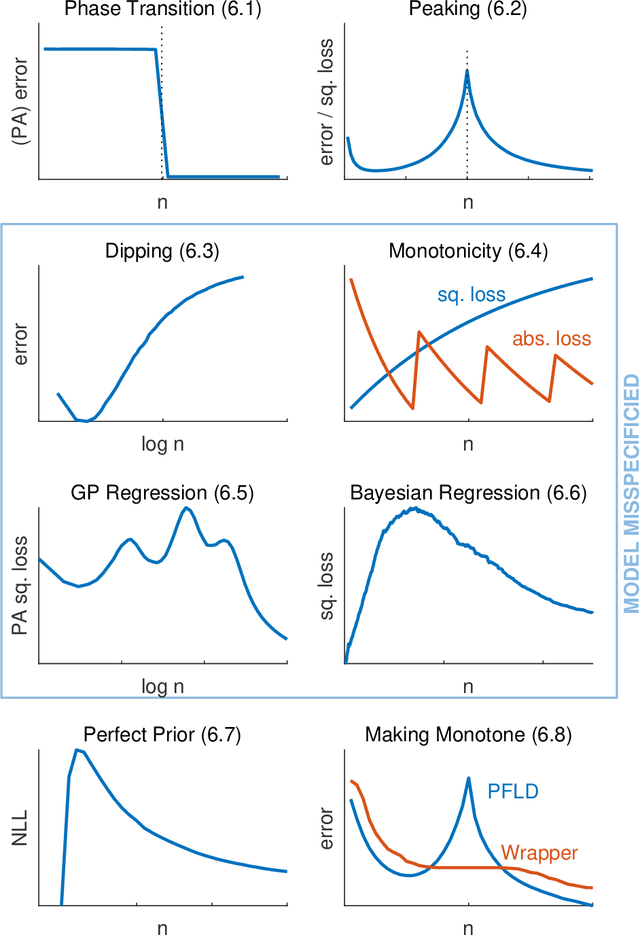
Learning curves provide insight into the dependence of a learner's generalization performance on the training set size. This important tool can be used for model selection, to predict the effect of more training data, and to reduce the computational complexity of model training and hyperparameter tuning. This review recounts the origins of the term, provides a formal definition of the learning curve, and briefly covers basics such as its estimation. Our main contribution is a comprehensive overview of the literature regarding the shape of learning curves. We discuss empirical and theoretical evidence that supports well-behaved curves that often have the shape of a power law or an exponential. We consider the learning curves of Gaussian processes, the complex shapes they can display, and the factors influencing them. We draw specific attention to examples of learning curves that are ill-behaved, showing worse learning performance with more training data. To wrap up, we point out various open problems that warrant deeper empirical and theoretical investigation. All in all, our review underscores that learning curves are surprisingly diverse and no universal model can be identified.