Enhancing Classifier Conservativeness and Robustness by Polynomiality
Paper and Code
Mar 23, 2022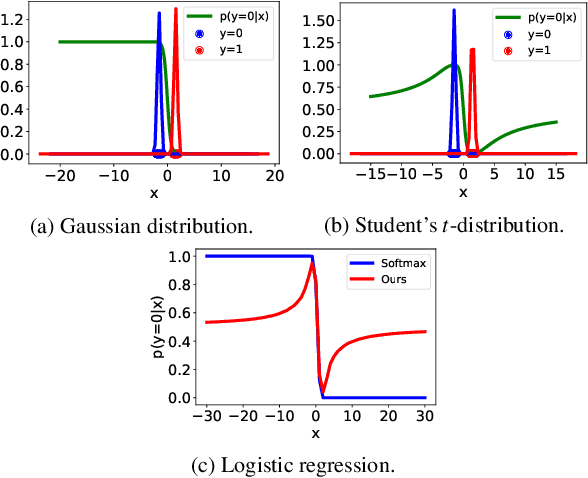
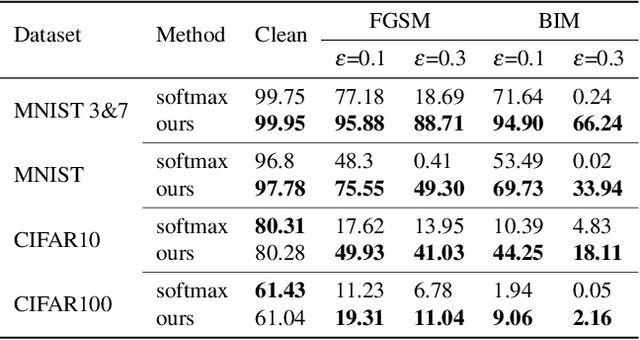
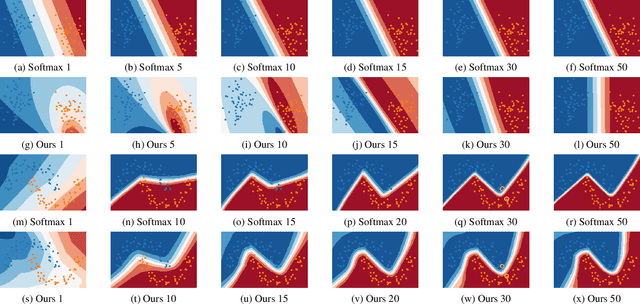
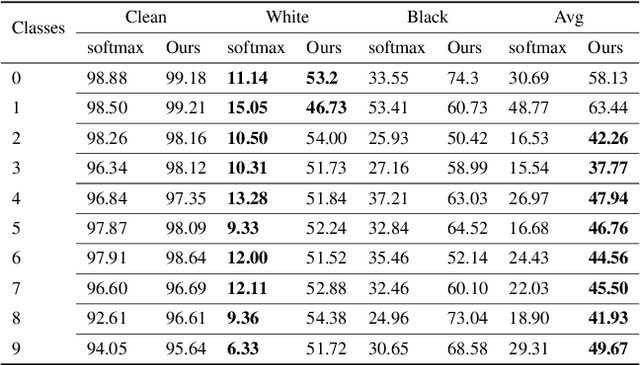
We illustrate the detrimental effect, such as overconfident decisions, that exponential behavior can have in methods like classical LDA and logistic regression. We then show how polynomiality can remedy the situation. This, among others, leads purposefully to random-level performance in the tails, away from the bulk of the training data. A directly related, simple, yet important technical novelty we subsequently present is softRmax: a reasoned alternative to the standard softmax function employed in contemporary (deep) neural networks. It is derived through linking the standard softmax to Gaussian class-conditional models, as employed in LDA, and replacing those by a polynomial alternative. We show that two aspects of softRmax, conservativeness and inherent gradient regularization, lead to robustness against adversarial attacks without gradient obfuscation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge