LCDB 1.1: A Database Illustrating Learning Curves Are More Ill-Behaved Than Previously Thought

Sample-wise learning curves plot performance versus training set size. They are useful for studying scaling laws and speeding up hyperparameter tuning and model selection. Learning curves are often assumed to be well-behaved: monotone (i.e. improving with more data) and convex. By constructing the Learning Curves Database 1.1 (LCDB 1.1), a large-scale database with high-resolution learning curves, we show that learning curves are less often well-behaved than previously thought. Using statistically rigorous methods, we observe significant ill-behavior in approximately 14% of the learning curves, almost twice as much as in previous estimates. We also identify which learners are to blame and show that specific learners are more ill-behaved than others. Additionally, we demonstrate that different feature scalings rarely resolve ill-behavior. We evaluate the impact of ill-behavior on downstream tasks, such as learning curve fitting and model selection, and find it poses significant challenges, underscoring the relevance and potential of LCDB 1.1 as a challenging benchmark for future research.

The Unreasonable Effectiveness Of Early Discarding After One Epoch In Neural Network Hyperparameter Optimization

To reach high performance with deep learning, hyperparameter optimization (HPO) is essential. This process is usually time-consuming due to costly evaluations of neural networks. Early discarding techniques limit the resources granted to unpromising candidates by observing the empirical learning curves and canceling neural network training as soon as the lack of competitiveness of a candidate becomes evident. Despite two decades of research, little is understood about the trade-off between the aggressiveness of discarding and the loss of predictive performance. Our paper studies this trade-off for several commonly used discarding techniques such as successive halving and learning curve extrapolation. Our surprising finding is that these commonly used techniques offer minimal to no added value compared to the simple strategy of discarding after a constant number of epochs of training. The chosen number of epochs depends mostly on the available compute budget. We call this approach i-Epoch (i being the constant number of epochs with which neural networks are trained) and suggest to assess the quality of early discarding techniques by comparing how their Pareto-Front (in consumed training epochs and predictive performance) complement the Pareto-Front of i-Epoch.

A Survey of Learning Curves with Bad Behavior: or How More Data Need Not Lead to Better Performance

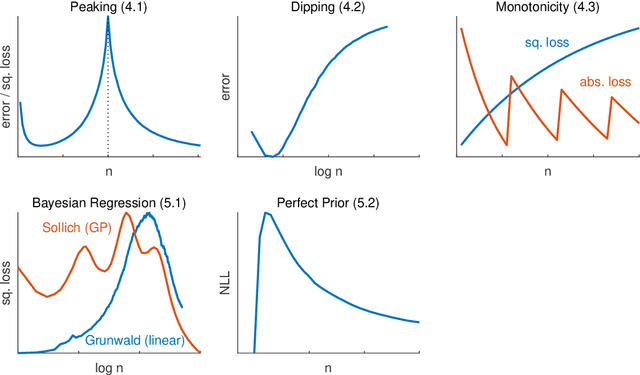
Plotting a learner's generalization performance against the training set size results in a so-called learning curve. This tool, providing insight in the behavior of the learner, is also practically valuable for model selection, predicting the effect of more training data, and reducing the computational complexity of training. We set out to make the (ideal) learning curve concept precise and briefly discuss the aforementioned usages of such curves. The larger part of this survey's focus, however, is on learning curves that show that more data does not necessarily leads to better generalization performance. A result that seems surprising to many researchers in the field of artificial intelligence. We point out the significance of these findings and conclude our survey with an overview and discussion of open problems in this area that warrant further theoretical and empirical investigation.

The Shape of Learning Curves: a Review

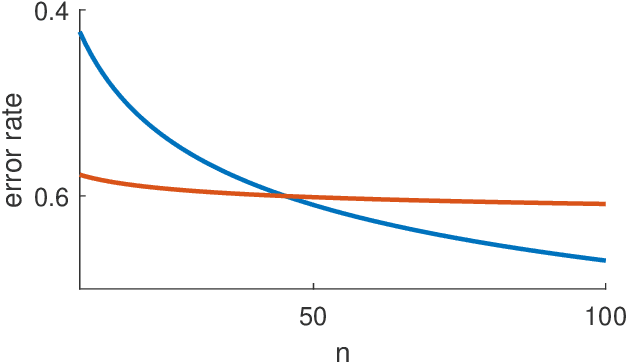
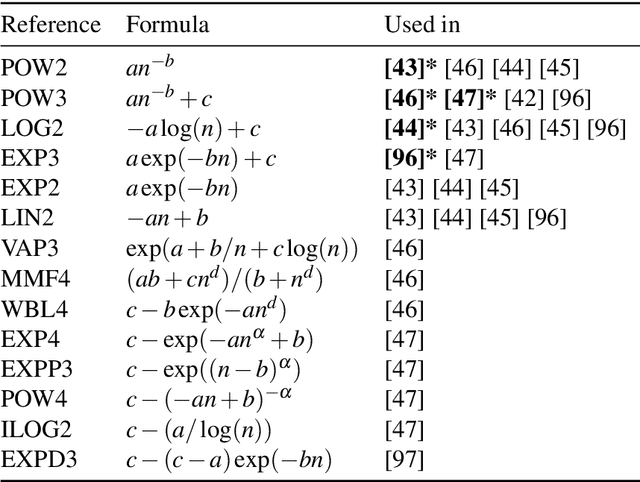
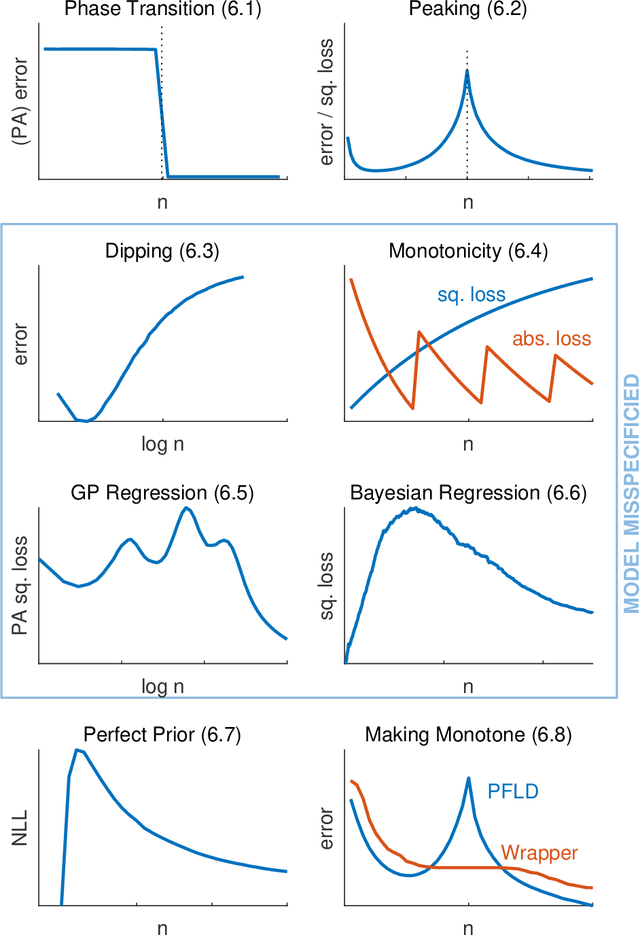
Learning curves provide insight into the dependence of a learner's generalization performance on the training set size. This important tool can be used for model selection, to predict the effect of more training data, and to reduce the computational complexity of model training and hyperparameter tuning. This review recounts the origins of the term, provides a formal definition of the learning curve, and briefly covers basics such as its estimation. Our main contribution is a comprehensive overview of the literature regarding the shape of learning curves. We discuss empirical and theoretical evidence that supports well-behaved curves that often have the shape of a power law or an exponential. We consider the learning curves of Gaussian processes, the complex shapes they can display, and the factors influencing them. We draw specific attention to examples of learning curves that are ill-behaved, showing worse learning performance with more training data. To wrap up, we point out various open problems that warrant deeper empirical and theoretical investigation. All in all, our review underscores that learning curves are surprisingly diverse and no universal model can be identified.

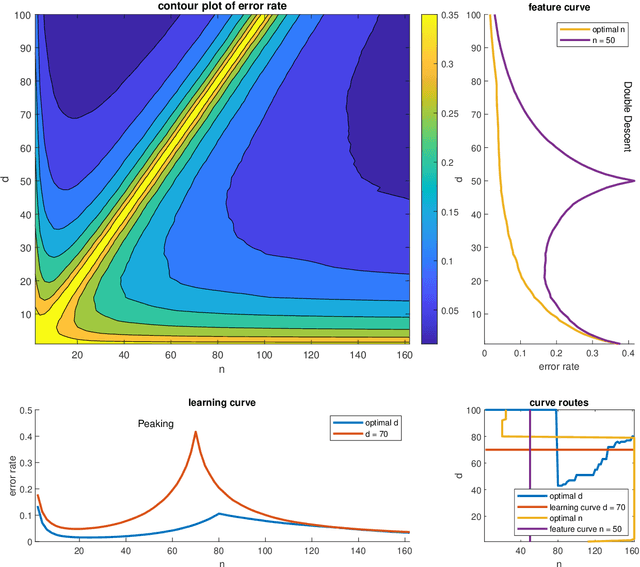
A Brief Prehistory of Double Descent

In their thought-provoking paper [1], Belkin et al. illustrate and discuss the shape of risk curves in the context of modern high-complexity learners. Given a fixed training sample size $n$, such curves show the risk of a learner as a function of some (approximate) measure of its complexity $N$. With $N$ the number of features, these curves are also referred to as feature curves. A salient observation in [1] is that these curves can display, what they call, double descent: with increasing $N$, the risk initially decreases, attains a minimum, and then increases until $N$ equals $n$, where the training data is fitted perfectly. Increasing $N$ even further, the risk decreases a second and final time, creating a peak at $N=n$. This twofold descent may come as a surprise, but as opposed to what [1] reports, it has not been overlooked historically. Our letter draws attention to some original, earlier findings, of interest to contemporary machine learning.

How to Manipulate CNNs to Make Them Lie: the GradCAM Case

Recently many methods have been introduced to explain CNN decisions. However, it has been shown that some methods can be sensitive to manipulation of the input. We continue this line of work and investigate the explanation method GradCAM. Instead of manipulating the input, we consider an adversary that manipulates the model itself to attack the explanation. By changing weights and architecture, we demonstrate that it is possible to generate any desired explanation, while leaving the model's accuracy essentially unchanged. This illustrates that GradCAM cannot explain the decision of every CNN and provides a proof of concept showing that it is possible to obfuscate the inner workings of a CNN. Finally, we combine input and model manipulation. To this end we put a backdoor in the network: the explanation is correct unless there is a specific pattern present in the input, which triggers a malicious explanation. Our work raises new security concerns, especially in settings where explanations of models may be used to make decisions, such as in the medical domain.

Minimizers of the Empirical Risk and Risk Monotonicity

Plotting a learner's average performance against the number of training samples results in a learning curve. Studying such curves on one or more data sets is a way to get to a better understanding of the generalization properties of this learner. The behavior of learning curves is, however, not very well understood and can display (for most researchers) quite unexpected behavior. Our work introduces the formal notion of \emph{risk monotonicity}, which asks the risk to not deteriorate with increasing training set sizes in expectation over the training samples. We then present the surprising result that various standard learners, specifically those that minimize the empirical risk, can act \emph{non}monotonically irrespective of the training sample size. We provide a theoretical underpinning for specific instantiations from classification, regression, and density estimation. Altogether, the proposed monotonicity notion opens up a whole new direction of research.

A Distribution Dependent and Independent Complexity Analysis of Manifold Regularization

Manifold regularization is a commonly used technique in semi-supervised learning. It guides the learning process by enforcing that the classification rule we find is smooth with respect to the data-manifold. In this paper we present sample and Rademacher complexity bounds for this method. We first derive distribution \emph{independent} sample complexity bounds by analyzing the general framework of adding a data dependent regularization term to a supervised learning process. We conclude that for these types of methods one can expect that the sample complexity improves at most by a constant, which depends on the hypothesis class. We then derive Rademacher complexities bounds which allow for a distribution \emph{dependent} complexity analysis. We illustrate how our bounds can be used for choosing an appropriate manifold regularization parameter. With our proposed procedure there is no need to use an additional labeled validation set.