Invariant Causal Prediction with Locally Linear Models

We consider the task of identifying the causal parents of a target variable among a set of candidate variables from observational data. Our main assumption is that the candidate variables are observed in different environments which may, for example, correspond to different settings of a machine or different time intervals in a dynamical process. Under certain assumptions different environments can be regarded as interventions on the observed system. We assume a linear relationship between target and covariates, which can be different in each environment with the only restriction that the causal structure is invariant across environments. This is an extension of the ICP ($\textbf{I}$nvariant $\textbf{C}$ausal $\textbf{P}$rediction) principle by Peters et al. [2016], who assumed a fixed linear relationship across all environments. Within our proposed setting we provide sufficient conditions for identifiability of the causal parents and introduce a practical method called LoLICaP ($\textbf{Lo}$cally $\textbf{L}$inear $\textbf{I}$nvariant $\textbf{Ca}$usal $\textbf{P}$rediction), which is based on a hypothesis test for parent identification using a ratio of minimum and maximum statistics. We then show in a simplified setting that the statistical power of LoLICaP converges exponentially fast in the sample size, and finally we analyze the behavior of LoLICaP experimentally in more general settings.

Loss Bounds for Approximate Influence-Based Abstraction

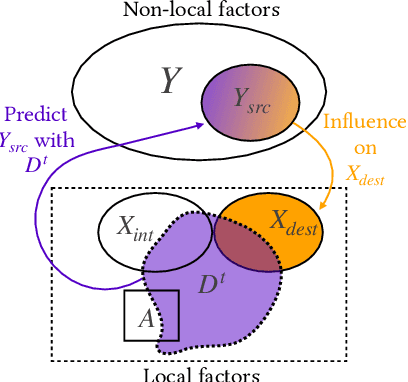
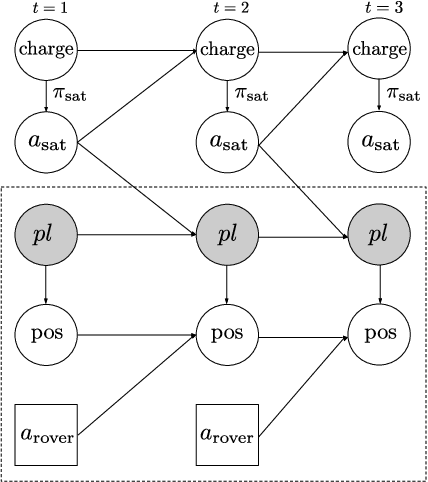
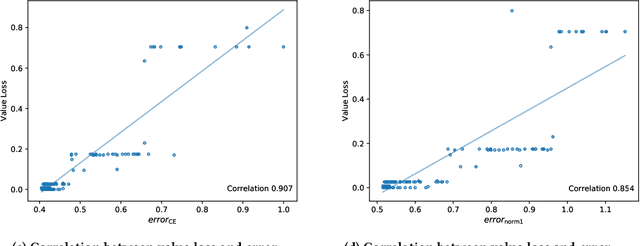
Sequential decision making techniques hold great promise to improve the performance of many real-world systems, but computational complexity hampers their principled application. Influence-based abstraction aims to gain leverage by modeling local subproblems together with the 'influence' that the rest of the system exerts on them. While computing exact representations of such influence might be intractable, learning approximate representations offers a promising approach to enable scalable solutions. This paper investigates the performance of such approaches from a theoretical perspective. The primary contribution is the derivation of sufficient conditions on approximate influence representations that can guarantee solutions with small value loss. In particular we show that neural networks trained with cross entropy are well suited to learn approximate influence representations. Moreover, we provide a sample based formulation of the bounds, which reduces the gap to applications. Finally, driven by our theoretical insights, we propose approximation error estimators, which empirically reveal to correlate well with the value loss.

A Note on High-Probability versus In-Expectation Guarantees of Generalization Bounds in Machine Learning

Statistical machine learning theory often tries to give generalization guarantees of machine learning models. Those models naturally underlie some fluctuation, as they are based on a data sample. If we were unlucky, and gathered a sample that is not representative of the underlying distribution, one cannot expect to construct a reliable machine learning model. Following that, statements made about the performance of machine learning models have to take the sampling process into account. The two common approaches for that are to generate statements that hold either in high-probability, or in-expectation, over the random sampling process. In this short note we show how one may transform one statement to another. As a technical novelty we address the case of unbounded loss function, where we use a fairly new assumption, called the witness condition.

A Brief Prehistory of Double Descent

In their thought-provoking paper [1], Belkin et al. illustrate and discuss the shape of risk curves in the context of modern high-complexity learners. Given a fixed training sample size $n$, such curves show the risk of a learner as a function of some (approximate) measure of its complexity $N$. With $N$ the number of features, these curves are also referred to as feature curves. A salient observation in [1] is that these curves can display, what they call, double descent: with increasing $N$, the risk initially decreases, attains a minimum, and then increases until $N$ equals $n$, where the training data is fitted perfectly. Increasing $N$ even further, the risk decreases a second and final time, creating a peak at $N=n$. This twofold descent may come as a surprise, but as opposed to what [1] reports, it has not been overlooked historically. Our letter draws attention to some original, earlier findings, of interest to contemporary machine learning.

Making Learners (More) Monotone

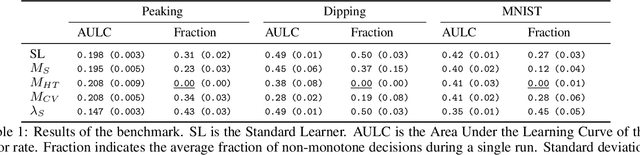
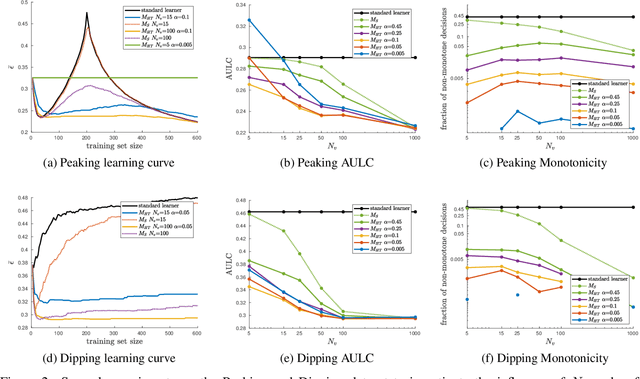
Learning performance can show non-monotonic behavior. That is, more data does not necessarily lead to better models, even on average. We propose three algorithms that take a supervised learning model and make it perform more monotone. We prove consistency and monotonicity with high probability, and evaluate the algorithms on scenarios where non-monotone behaviour occurs. Our proposed algorithm $\text{MT}_{\text{HT}}$ makes less than $1\%$ non-monotone decisions on MNIST while staying competitive in terms of error rate compared to several baselines.

Consistency and Finite Sample Behavior of Binary Class Probability Estimation

In this work we investigate to which extent one can recover class probabilities within the empirical risk minimization (ERM) paradigm. The main aim of our paper is to extend existing results and emphasize the tight relations between empirical risk minimization and class probability estimation. Based on existing literature on excess risk bounds and proper scoring rules, we derive a class probability estimator based on empirical risk minimization. We then derive fairly general conditions under which this estimator will converge, in the L1-norm and in probability, to the true class probabilities. Our main contribution is to present a way to derive finite sample L1-convergence rates of this estimator for different surrogate loss functions. We also study in detail which commonly used loss functions are suitable for this estimation problem and finally discuss the setting of model-misspecification as well as a possible extension to asymmetric loss functions.

Improvability Through Semi-Supervised Learning: A Survey of Theoretical Results

Semi-supervised learning is a setting in which one has labeled and unlabeled data available. In this survey we explore different types of theoretical results when one uses unlabeled data in classification and regression tasks. Most methods that use unlabeled data rely on certain assumptions about the data distribution. When those assumptions are not met in reality, including unlabeled data may actually decrease performance. Studying such methods, it therefore is particularly important to have an understanding of the underlying theory. In this review we gather results about the possible gains one can achieve when using semi-supervised learning as well as results about the limits of such methods. More precisely, this review collects the answers to the following questions: What are, in terms of improving supervised methods, the limits of semi-supervised learning? What are the assumptions of different methods? What can we achieve if the assumptions are true? Finally, we also discuss the biggest bottleneck of semi-supervised learning, namely the assumptions they make.

Minimizers of the Empirical Risk and Risk Monotonicity

Plotting a learner's average performance against the number of training samples results in a learning curve. Studying such curves on one or more data sets is a way to get to a better understanding of the generalization properties of this learner. The behavior of learning curves is, however, not very well understood and can display (for most researchers) quite unexpected behavior. Our work introduces the formal notion of \emph{risk monotonicity}, which asks the risk to not deteriorate with increasing training set sizes in expectation over the training samples. We then present the surprising result that various standard learners, specifically those that minimize the empirical risk, can act \emph{non}monotonically irrespective of the training sample size. We provide a theoretical underpinning for specific instantiations from classification, regression, and density estimation. Altogether, the proposed monotonicity notion opens up a whole new direction of research.

A Distribution Dependent and Independent Complexity Analysis of Manifold Regularization

Manifold regularization is a commonly used technique in semi-supervised learning. It guides the learning process by enforcing that the classification rule we find is smooth with respect to the data-manifold. In this paper we present sample and Rademacher complexity bounds for this method. We first derive distribution \emph{independent} sample complexity bounds by analyzing the general framework of adding a data dependent regularization term to a supervised learning process. We conclude that for these types of methods one can expect that the sample complexity improves at most by a constant, which depends on the hypothesis class. We then derive Rademacher complexities bounds which allow for a distribution \emph{dependent} complexity analysis. We illustrate how our bounds can be used for choosing an appropriate manifold regularization parameter. With our proposed procedure there is no need to use an additional labeled validation set.

Semi-Supervised Learning, Causality and the Conditional Cluster Assumption

While the success of semi-supervised learning (SSL) is still not fully understood, Sch\"olkopf et al. (2012) have established a link to the principle of independent causal mechanisms. They conclude that SSL should be impossible when predicting a target variable from its causes, but possible when predicting it from its effects. Since both these cases are somewhat restrictive, we extend their work by considering classification using cause and effect features at the same time, such as predicting a disease from both risk factors and symptoms. While standard SSL exploits information contained in the marginal distribution of the inputs (to improve our estimate of the conditional distribution of target given inputs), we argue that in our more general setting we can use information in the conditional of effect features given causal features. We explore how this insight generalizes the previous understanding, and how it relates to and can be exploited for SSL.