Loss Bounds for Approximate Influence-Based Abstraction
Paper and Code
Nov 03, 2020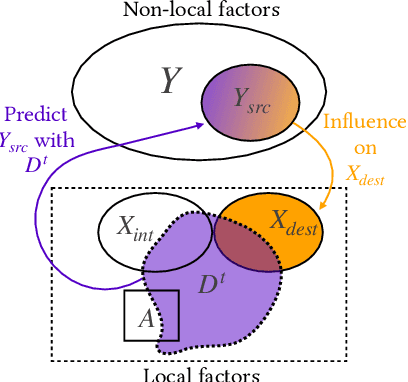
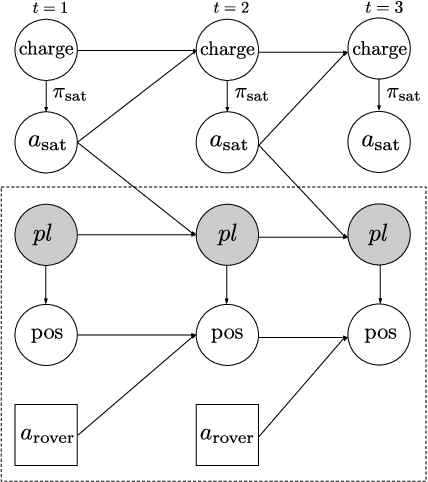
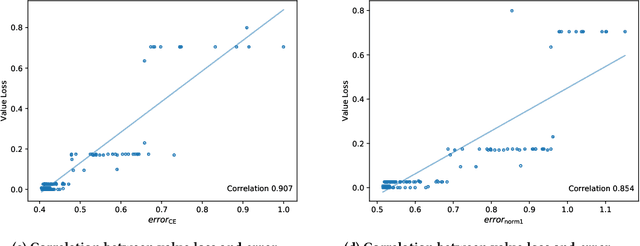
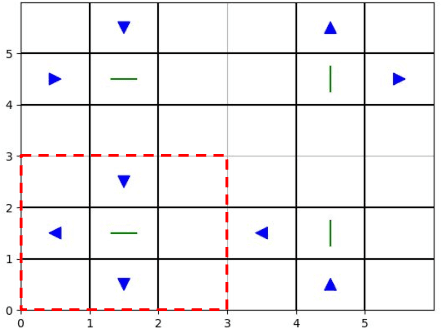
Sequential decision making techniques hold great promise to improve the performance of many real-world systems, but computational complexity hampers their principled application. Influence-based abstraction aims to gain leverage by modeling local subproblems together with the 'influence' that the rest of the system exerts on them. While computing exact representations of such influence might be intractable, learning approximate representations offers a promising approach to enable scalable solutions. This paper investigates the performance of such approaches from a theoretical perspective. The primary contribution is the derivation of sufficient conditions on approximate influence representations that can guarantee solutions with small value loss. In particular we show that neural networks trained with cross entropy are well suited to learn approximate influence representations. Moreover, we provide a sample based formulation of the bounds, which reduces the gap to applications. Finally, driven by our theoretical insights, we propose approximation error estimators, which empirically reveal to correlate well with the value loss.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge