MalTree: Tracing Malware Evolution from Embeddings at Scale

Malware detection remains largely reactive: machine learning models trained on known samples degrade as threats evolve. Understanding evolutionary relationships among malware families can inform proactive defense, but traditional reverse engineering can take months to years to uncover such lineage relationships. We propose MalTree, a framework that applies bioinformatics inspired phylogenetic techniques (UPGMA and Neighbor-Joining) at scale to model malware evolution automatically using structural, behavioral, and image-based features. We introduce temporal validation using VirusTotal timestamps to assess whether inferred trees reflect actual evolutionary order. MalTree achieves 87% temporal consistency, indicating that inferred evolutionary relationships closely align with real-world emergence timelines. Our analysis shows that some families mutate over 10 times faster than others, suggesting that detection strategies should be tailored to family-specific evolutionary tempos. Case studies, including the Mirai botnet, confirm that inferred relationships from our phylogenetic tree align with documented threat intelligence. Our framework provides a foundation for shifting malware analysis from sample-by-sample classification toward lineage-aware evolutionary modeling.

Making Learners (More) Monotone

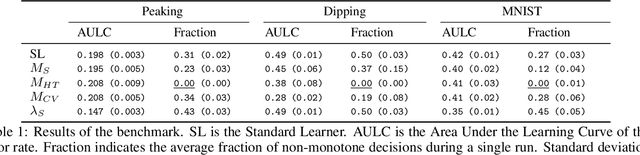
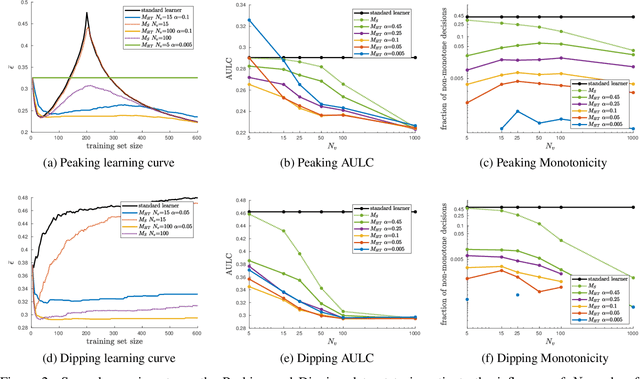
Learning performance can show non-monotonic behavior. That is, more data does not necessarily lead to better models, even on average. We propose three algorithms that take a supervised learning model and make it perform more monotone. We prove consistency and monotonicity with high probability, and evaluate the algorithms on scenarios where non-monotone behaviour occurs. Our proposed algorithm $\text{MT}_{\text{HT}}$ makes less than $1\%$ non-monotone decisions on MNIST while staying competitive in terms of error rate compared to several baselines.

Nuclear Discrepancy for Active Learning

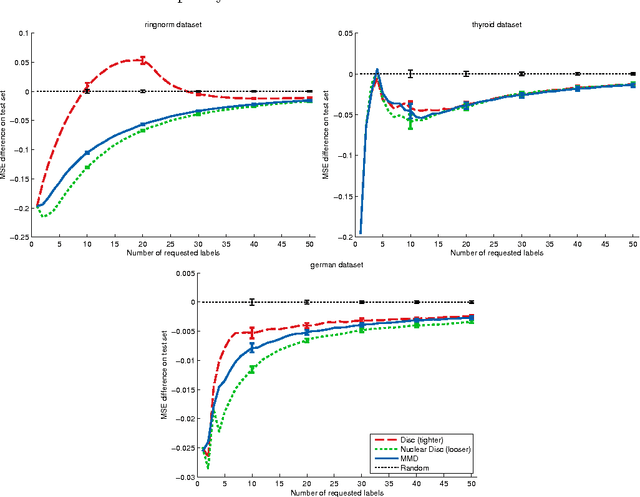
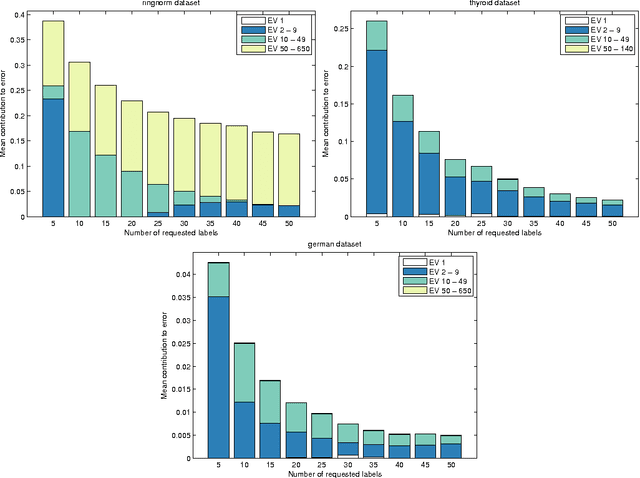
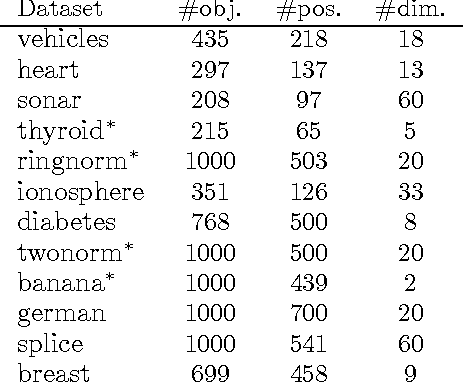
Active learning algorithms propose which unlabeled objects should be queried for their labels to improve a predictive model the most. We study active learners that minimize generalization bounds and uncover relationships between these bounds that lead to an improved approach to active learning. In particular we show the relation between the bound of the state-of-the-art Maximum Mean Discrepancy (MMD) active learner, the bound of the Discrepancy, and a new and looser bound that we refer to as the Nuclear Discrepancy bound. We motivate this bound by a probabilistic argument: we show it considers situations which are more likely to occur. Our experiments indicate that active learning using the tightest Discrepancy bound performs the worst in terms of the squared loss. Overall, our proposed loosest Nuclear Discrepancy generalization bound performs the best. We confirm our probabilistic argument empirically: the other bounds focus on more pessimistic scenarios that are rarer in practice. We conclude that tightness of bounds is not always of main importance and that active learning methods should concentrate on realistic scenarios in order to improve performance.