Inductive Conformal Prediction under Data Scarcity: Exploring the Impacts of Nonconformity Measures
Paper and Code
Oct 13, 2024

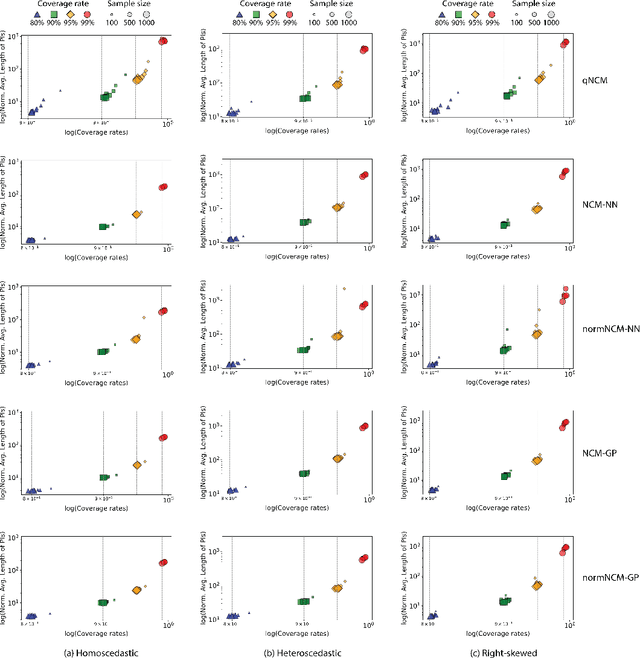

Conformal prediction, which makes no distributional assumptions about the data, has emerged as a powerful and reliable approach to uncertainty quantification in practical applications. The nonconformity measure used in conformal prediction quantifies how a test sample differs from the training data and the effectiveness of a conformal prediction interval may depend heavily on the precise measure employed. The impact of this choice has, however, not been widely explored, especially when dealing with limited amounts of data. The primary objective of this study is to evaluate the performance of various nonconformity measures (absolute error-based, normalized absolute error-based, and quantile-based measures) in terms of validity and efficiency when used in inductive conformal prediction. The focus is on small datasets, which is still a common setting in many real-world applications. Using synthetic and real-world data, we assess how different characteristics -- such as dataset size, noise, and dimensionality -- can affect the efficiency of conformal prediction intervals. Our results show that although there are differences, no single nonconformity measure consistently outperforms the others, as the effectiveness of each nonconformity measure is heavily influenced by the specific nature of the data. Additionally, we found that increasing dataset size does not always improve efficiency, suggesting the importance of fine-tuning models and, again, the need to carefully select the nonconformity measure for different applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge