Attenuation-adjusted deep learning of pore defects in 2D radiographs of additive manufacturing powders

The presence of gas pores in metal feedstock powder for additive manufacturing greatly affects the final AM product. Since current porosity analysis often involves lengthy X-ray computed tomography (XCT) scans with a full rotation around the sample, motivation exists to explore methods that allow for high throughput -- possibly enabling in-line porosity analysis during manufacturing. Through labelling pore pixels on single 2D radiographs of powders, this work seeks to simulate such future efficient setups. High segmentation accuracy is achieved by combining a model of X-ray attenuation through particles with a variant of the widely applied UNet architecture; notably, F1-score increases by $11.4\%$ compared to the baseline UNet. The proposed pore segmentation is enabled by: 1) pretraining on synthetic data, 2) making tight particle cutouts, and 3) subtracting an ideal particle without pores generated from a distance map inspired by Lambert-Beers law. This paper explores four image processing methods, where the fastest (yet still unoptimized) segments a particle in mean $0.014s$ time with F1-score $0.78$, and the most accurate in $0.291s$ with F1-score $0.87$. Due to their scalable nature, these strategies can be involved in making high throughput porosity analysis of metal feedstock powder for additive manufacturing.

Statistical investigations into the geometry and homology of random programs

AI-supported programming has taken giant leaps with tools such as Meta's Llama and openAI's chatGPT. These are examples of stochastic sources of programs and have already greatly influenced how we produce code and teach programming. If we consider input to such models as a stochastic source, a natural question is, what is the relation between the input and the output distributions, between the chatGPT prompt and the resulting program? In this paper, we will show how the relation between random Python programs generated from chatGPT can be described geometrically and topologically using Tree-edit distances between the program's syntax trees and without explicit modeling of the underlying space. A popular approach to studying high-dimensional samples in a metric space is to use low-dimensional embedding using, e.g., multidimensional scaling. Such methods imply errors depending on the data and dimension of the embedding space. In this article, we propose to restrict such projection methods to purely visualization purposes and instead use geometric summary statistics, methods from spatial point statistics, and topological data analysis to characterize the configurations of random programs that do not rely on embedding approximations. To demonstrate their usefulness, we compare two publicly available models: ChatGPT-4 and TinyLlama, on a simple problem related to image processing. Application areas include understanding how questions should be asked to obtain useful programs; measuring how consistently a given large language model answers; and comparing the different large language models as a programming assistant. Finally, we speculate that our approach may in the future give new insights into the structure of programming languages.

Locally orderless networks

We present Locally Orderless Networks (LON) and its theoretic foundation which links it to Convolutional Neural Networks (CNN), to Scale-space histograms, and measurement theory. The key elements are a regular sampling of the bias and the derivative of the activation function. We compare LON, CNN, and Scale-space histograms on prototypical single-layer networks. We show how LON and CNN can emulate each other, how LON expands the set of functionals computable to non-linear functions such as squaring. We demonstrate simple networks which illustrate the improved performance of LON over CNN on simple tasks for estimating the gradient magnitude squared, for regressing shape area and perimeter lengths, and for explainability of individual pixels' influence on the result.

Morphology on categorical distributions

The categorical distribution is a natural representation of uncertainty in multi-class segmentations. In the two-class case the categorical distribution reduces to the Bernoulli distribution, for which grayscale morphology provides a range of useful operations. In the general case, applying morphological operations on uncertain multi-class segmentations is not straightforward as an image of categorical distributions is not a complete lattice. Although morphology on color images has received wide attention, this is not so for color-coded or categorical images and even less so for images of categorical distributions. In this work, we establish a set of requirements for morphology on categorical distributions by combining classic morphology with a probabilistic view. We then define operators respecting these requirements, introduce protected operations on categorical distributions and illustrate the utility of these operators on two example tasks: modeling annotator bias in brain tumor segmentations and segmenting vesicle instances from the predictions of a multi-class U-Net.

Measuring shape relations using r-parallel sets

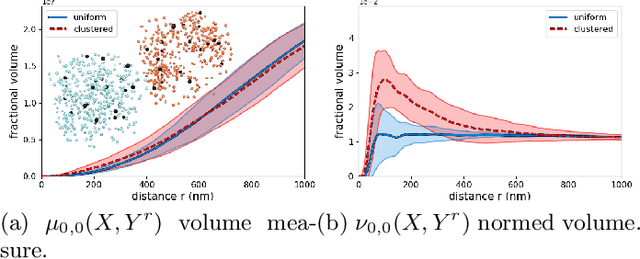
Geometrical measurements of biological objects form the basis of many quantitative analyses. Hausdorff measures such as the volume and the area of objects are simple and popular descriptors of individual objects, however, for most biological processes, the interaction between objects cannot be ignored, and the shape and function of neighboring objects are mutually influential. In this paper, we present a theory on the geometrical interaction between objects based on the theory of spatial point processes. Our theory is based on the relation between two objects: a reference and an observed object. We generate the $r$-parallel sets of the reference object, we calculate the intersection between the $r$-parallel sets and the observed object, and we define measures on these intersections. Our measures are simple like the volume and area of an object, but describe further details about the shape of individual objects and their pairwise geometrical relation. Finally, we propose a summary statistics for collections of shapes and their interaction. We evaluate these measures on a publicly available FIB-SEM 3D data set of an adult rodent.

Locally Orderless Registration

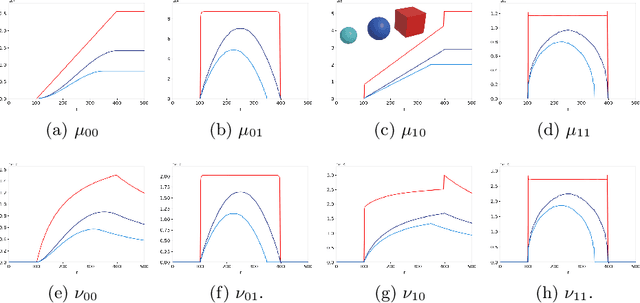
Image registration is an important tool for medical image analysis and is used to bring images into the same reference frame by warping the coordinate field of one image, such that some similarity measure is minimized. We study similarity in image registration in the context of Locally Orderless Images (LOI), which is the natural way to study density estimates and reveals the 3 fundamental scales: the measurement scale, the intensity scale, and the integration scale. This paper has three main contributions: Firstly, we rephrase a large set of popular similarity measures into a common framework, which we refer to as Locally Orderless Registration, and which makes full use of the features of local histograms. Secondly, we extend the theoretical understanding of the local histograms. Thirdly, we use our framework to compare two state-of-the-art intensity density estimators for image registration: The Parzen Window (PW) and the Generalized Partial Volume (GPV), and we demonstrate their differences on a popular similarity measure, Normalized Mutual Information (NMI). We conclude, that complicated similarity measures such as NMI may be evaluated almost as fast as simple measures such as Sum of Squared Distances (SSD) regardless of the choice of PW and GPV. Also, GPV is an asymmetric measure, and PW is our preferred choice.