Measuring shape relations using r-parallel sets

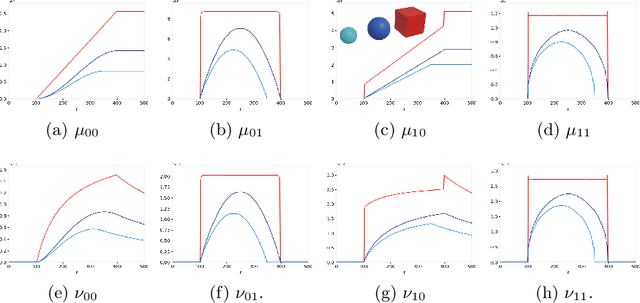
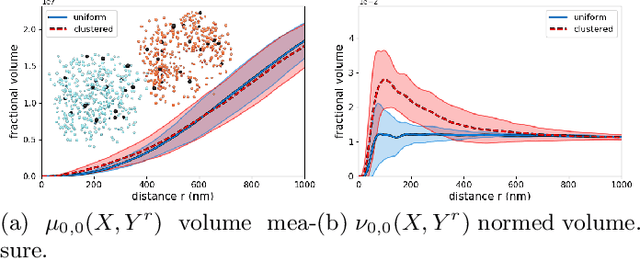
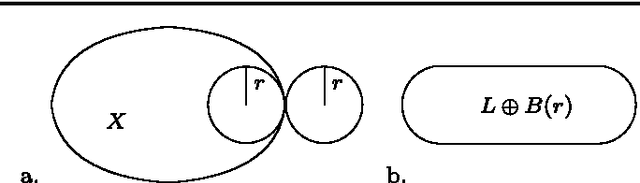
Geometrical measurements of biological objects form the basis of many quantitative analyses. Hausdorff measures such as the volume and the area of objects are simple and popular descriptors of individual objects, however, for most biological processes, the interaction between objects cannot be ignored, and the shape and function of neighboring objects are mutually influential. In this paper, we present a theory on the geometrical interaction between objects based on the theory of spatial point processes. Our theory is based on the relation between two objects: a reference and an observed object. We generate the $r$-parallel sets of the reference object, we calculate the intersection between the $r$-parallel sets and the observed object, and we define measures on these intersections. Our measures are simple like the volume and area of an object, but describe further details about the shape of individual objects and their pairwise geometrical relation. Finally, we propose a summary statistics for collections of shapes and their interaction. We evaluate these measures on a publicly available FIB-SEM 3D data set of an adult rodent.

Estimation of intrinsic volumes from digital grey-scale images

Local algorithms are common tools for estimating intrinsic volumes from black-and-white digital images. However, these algorithms are typically biased in the design based setting, even when the resolution tends to infinity. Moreover, images recorded in practice are most often blurred grey-scale images rather than black-and-white. In this paper, an extended definition of local algorithms, applying directly to grey-scale images without thresholding, is suggested. We investigate the asymptotics of these new algorithms when the resolution tends to infinity and apply this to construct estimators for surface area and integrated mean curvature that are asymptotically unbiased in certain natural settings.