Patch-based image Super Resolution using generalized Gaussian mixture model

Single Image Super Resolution (SISR) methods aim to recover the clean images in high resolution from low resolution observations.A family of patch-based approaches have received considerable attention and development. The minimum mean square error (MMSE) methodis a powerful image restoration method that uses a probability model on the patches of images. This paper proposes an algorithm to learn a jointgeneralized Gaussian mixture model (GGMM) from a pair of the low resolution patches and the corresponding high resolution patches fromthe reference data. We then reconstruct the high resolution image based on the MMSE method. Our numerical evaluations indicate that theMMSE-GGMM method competes with other state of the art methods.

Fast off-the-grid sparse recovery with over-parametrized projected gradient descent

We consider the problem of recovering off-the-grid spikes from Fourier measurements. Successful methods such as sliding Frank-Wolfe and continuous orthogonal matching pursuit (OMP) iteratively add spikes to the solution then perform a costly (when the number of spikes is large) descent on all parameters at each iteration. In 2D, it was shown that performing a projected gradient descent (PGD) from a gridded over-parametrized initialization was faster than continuous orthogonal matching pursuit. In this paper, we propose an off-the-grid over-parametrized initialization of the PGD based on OMP that permits to fully avoid grids and gives faster results in 3D.

LU-Net: An Efficient Network for 3D LiDAR Point Cloud Semantic Segmentation Based on End-to-End-Learned 3D Features and U-Net

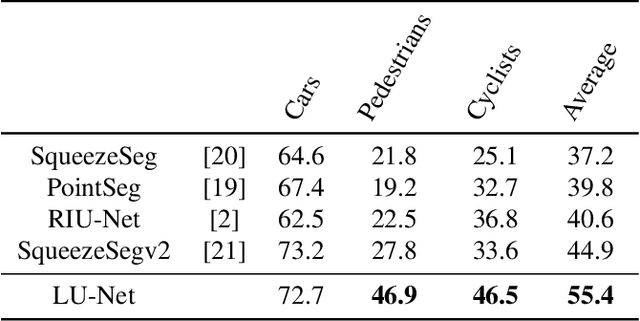
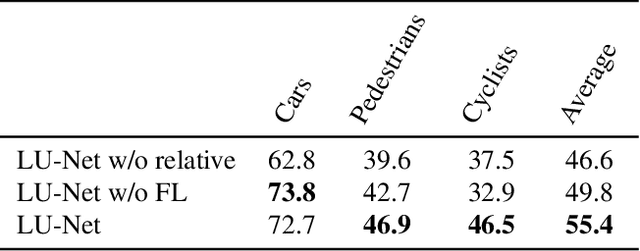
We propose LU-Net -- for LiDAR U-Net, a new method for the semantic segmentation of a 3D LiDAR point cloud. Instead of applying some global 3D segmentation method such as PointNet, we propose an end-to-end architecture for LiDAR point cloud semantic segmentation that efficiently solves the problem as an image processing problem. We first extract high-level 3D features for each point given its 3D neighbors. Then, these features are projected into a 2D multichannel range-image by considering the topology of the sensor. Thanks to these learned features and this projection, we can finally perform the segmentation using a simple U-Net segmentation network, which performs very well while being very efficient. In this way, we can exploit both the 3D nature of the data and the specificity of the LiDAR sensor. This approach outperforms the state-of-the-art by a large margin on the KITTI dataset, as our experiments show. Moreover, this approach operates at 24fps on a single GPU. This is above the acquisition rate of common LiDAR sensors which makes it suitable for real-time applications.

RIU-Net: Embarrassingly simple semantic segmentation of 3D LiDAR point cloud

This paper proposes RIU-Net (for Range-Image U-Net), the adaptation of a popular semantic segmentation network for the semantic segmentation of a 3D LiDAR point cloud. The point cloud is turned into a 2D range-image by exploiting the topology of the sensor. This image is then used as input to a U-net. This architecture has already proved its efficiency for the task of semantic segmentation of medical images. We demonstrate how it can also be used for the accurate semantic segmentation of a 3D LiDAR point cloud and how it represents a valid bridge between image processing and 3D point cloud processing. Our model is trained on range-images built from KITTI 3D object detection dataset. Experiments show that RIU-Net, despite being very simple, offers results that are comparable to the state-of-the-art of range-image based methods. Finally, we demonstrate that this architecture is able to operate at 90fps on a single GPU, which enables deployment for real-time segmentation.

Variational Methods for Normal Integration

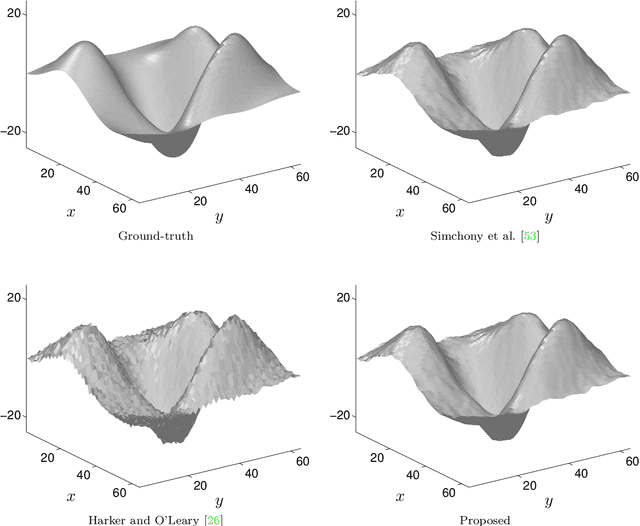
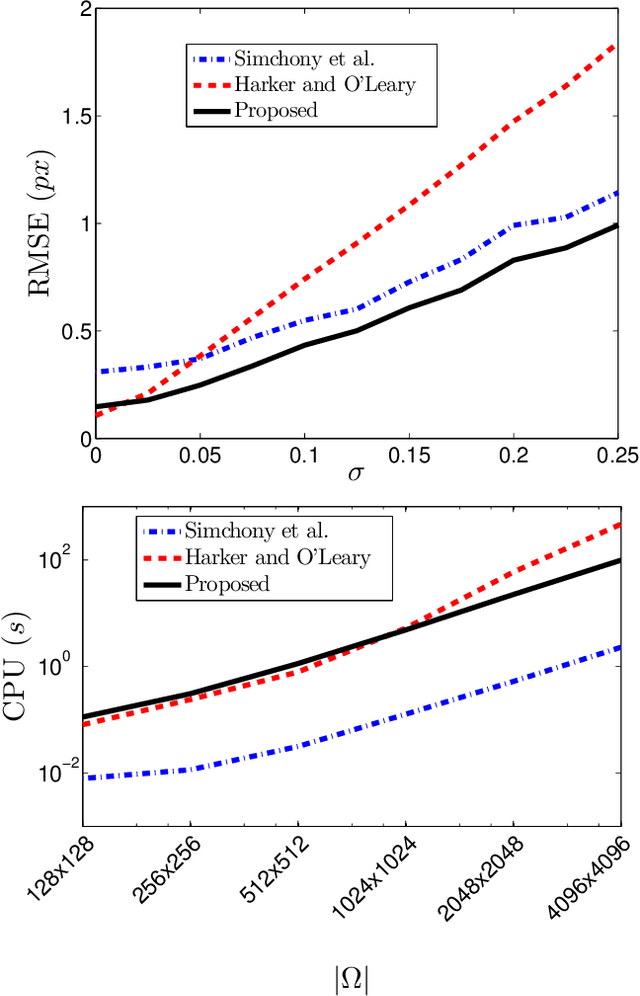
The need for an efficient method of integration of a dense normal field is inspired by several computer vision tasks, such as shape-from-shading, photometric stereo, deflectometry, etc. Inspired by edge-preserving methods from image processing, we study in this paper several variational approaches for normal integration, with a focus on non-rectangular domains, free boundary and depth discontinuities. We first introduce a new discretization for quadratic integration, which is designed to ensure both fast recovery and the ability to handle non-rectangular domains with a free boundary. Yet, with this solver, discontinuous surfaces can be handled only if the scene is first segmented into pieces without discontinuity. Hence, we then discuss several discontinuity-preserving strategies. Those inspired, respectively, by the Mumford-Shah segmentation method and by anisotropic diffusion, are shown to be the most effective for recovering discontinuities.

Normal Integration: A Survey

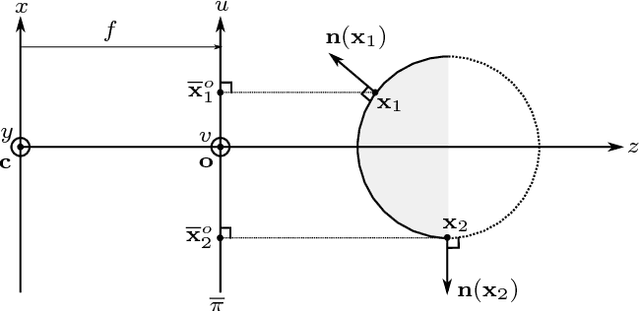
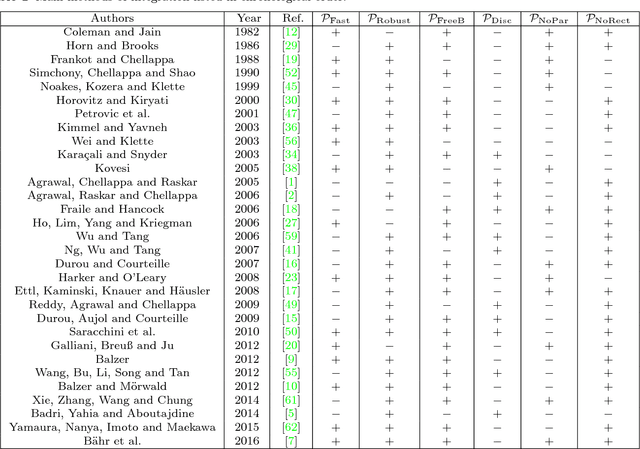
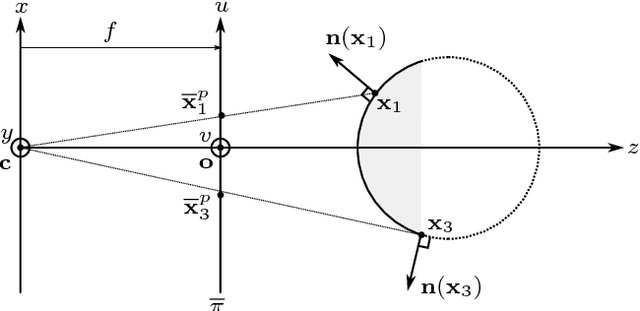
The need for efficient normal integration methods is driven by several computer vision tasks such as shape-from-shading, photometric stereo, deflectometry, etc. In the first part of this survey, we select the most important properties that one may expect from a normal integration method, based on a thorough study of two pioneering works by Horn and Brooks [28] and by Frankot and Chellappa [19]. Apart from accuracy, an integration method should at least be fast and robust to a noisy normal field. In addition, it should be able to handle several types of boundary condition, including the case of a free boundary, and a reconstruction domain of any shape i.e., which is not necessarily rectangular. It is also much appreciated that a minimum number of parameters have to be tuned, or even no parameter at all. Finally, it should preserve the depth discontinuities. In the second part of this survey, we review most of the existing methods in view of this analysis, and conclude that none of them satisfies all of the required properties. This work is complemented by a companion paper entitled Variational Methods for Normal Integration, in which we focus on the problem of normal integration in the presence of depth discontinuities, a problem which occurs as soon as there are occlusions.

Regularized Discrete Optimal Transport

This article introduces a generalization of the discrete optimal transport, with applications to color image manipulations. This new formulation includes a relaxation of the mass conservation constraint and a regularization term. These two features are crucial for image processing tasks, which necessitate to take into account families of multimodal histograms, with large mass variation across modes. The corresponding relaxed and regularized transportation problem is the solution of a convex optimization problem. Depending on the regularization used, this minimization can be solved using standard linear programming methods or first order proximal splitting schemes. The resulting transportation plan can be used as a color transfer map, which is robust to mass variation across images color palettes. Furthermore, the regularization of the transport plan helps to remove colorization artifacts due to noise amplification. We also extend this framework to the computation of barycenters of distributions. The barycenter is the solution of an optimization problem, which is separately convex with respect to the barycenter and the transportation plans, but not jointly convex. A block coordinate descent scheme converges to a stationary point of the energy. We show that the resulting algorithm can be used for color normalization across several images. The relaxed and regularized barycenter defines a common color palette for those images. Applying color transfer toward this average palette performs a color normalization of the input images.