Parameter-free structure-texture image decomposition by unrolling

In this work, we propose a parameter-free and efficient method to tackle the structure-texture image decomposition problem. In particular, we present a neural network LPR-NET based on the unrolling of the Low Patch Rank model. On the one hand, this allows us to automatically learn parameters from data, and on the other hand to be computationally faster while obtaining qualitatively similar results compared to traditional iterative model-based methods. Moreover, despite being trained on synthetic images, numerical experiments show the ability of our network to generalize well when applied to natural images.

Towards optimal algorithms for the recovery of low-dimensional models with linear rates

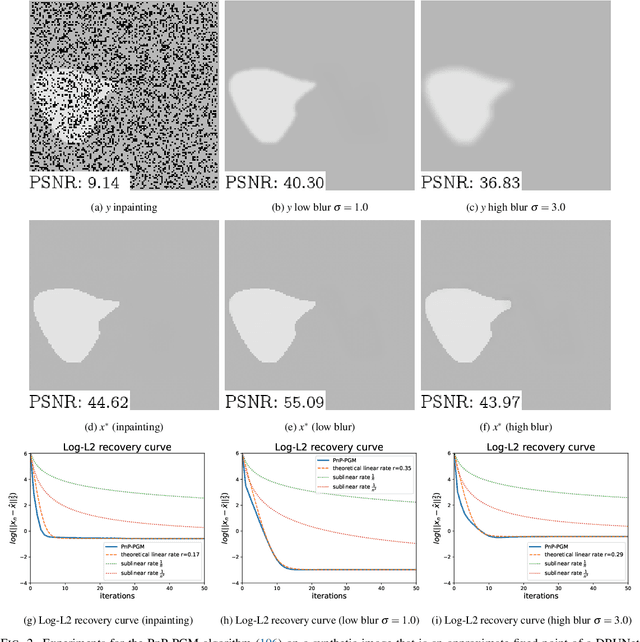
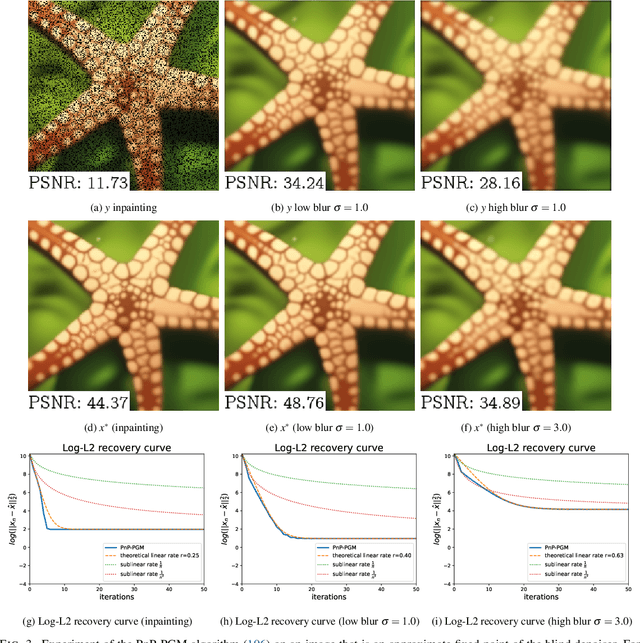
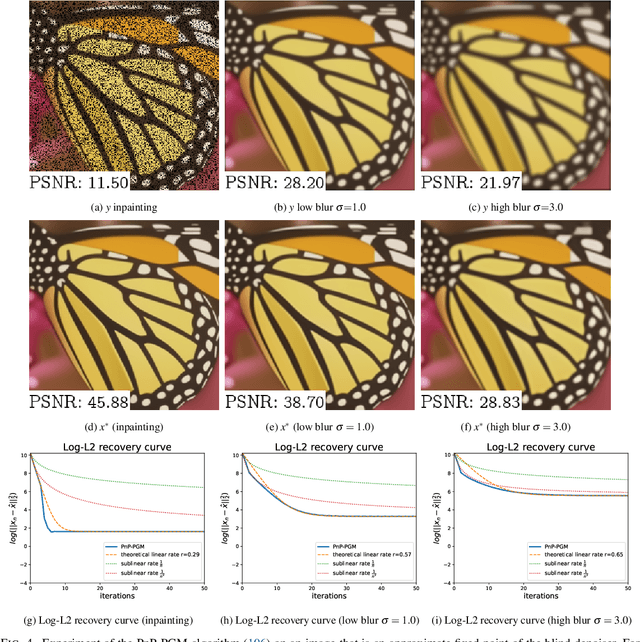
We consider the problem of recovering elements of a low-dimensional model from linear measurements. From signal and image processing to inverse problems in data science, this question has been at the center of many applications. Lately, with the success of models and methods relying on deep neural networks leading to non-convex formulations, traditional convex variational approaches have shown their limits. Furthermore, the multiplication of algorithms and recovery results makes identifying the best methods a complex task. In this article, we study recovery with a class of widely used algorithms without considering any underlying functional. This result leads to a class of projected gradient descent algorithms that recover a given low-dimensional with linear rates. The obtained rates decouple the impact of the quality of the measurements with respect to the model from its intrinsic complexity. As a consequence, we can directly measure the performance of this class of projected gradient descents through a restricted Lipschitz constant of the projection. By optimizing this constant, we define optimal algorithms. Our general approach provides an optimality result in the case of sparse recovery. Moreover, we uncover underlying linear rates of convergence for some ''plug and play'' imaging methods relying on deep priors by interpreting our results in this context, thus linking low-dimensional recovery and recovery with deep priors under a unified theory, validated by experiments on synthetic and real data.