From sparse recovery to plug-and-play priors, understanding trade-offs for stable recovery with generalized projected gradient descent

We consider the problem of recovering an unknown low-dimensional vector from noisy, underdetermined observations. We focus on the Generalized Projected Gradient Descent (GPGD) framework, which unifies traditional sparse recovery methods and modern approaches using learned deep projective priors. We extend previous convergence results to robustness to model and projection errors. We use these theoretical results to explore ways to better control stability and robustness constants. To reduce recovery errors due to measurement noise, we consider generalized back-projection strategies to adapt GPGD to structured noise, such as sparse outliers. To improve the stability of GPGD, we propose a normalized idempotent regularization for the learning of deep projective priors. We provide numerical experiments in the context of sparse recovery and image inverse problems, highlighting the trade-offs between identifiability and stability that can be achieved with such methods.

Stochastic Orthogonal Regularization for deep projective priors

Many crucial tasks of image processing and computer vision are formulated as inverse problems. Thus, it is of great importance to design fast and robust algorithms to solve these problems. In this paper, we focus on generalized projected gradient descent (GPGD) algorithms where generalized projections are realized with learned neural networks and provide state-of-the-art results for imaging inverse problems. Indeed, neural networks allow for projections onto unknown low-dimensional sets that model complex data, such as images. We call these projections deep projective priors. In generic settings, when the orthogonal projection onto a lowdimensional model set is used, it has been shown, under a restricted isometry assumption, that the corresponding orthogonal PGD converges with a linear rate, yielding near-optimal convergence (within the class of GPGD methods) in the classical case of sparse recovery. However, for deep projective priors trained with classical mean squared error losses, there is little guarantee that the hypotheses for linear convergence are satisfied. In this paper, we propose a stochastic orthogonal regularization of the training loss for deep projective priors. This regularization is motivated by our theoretical results: a sufficiently good approximation of the orthogonal projection guarantees linear stable recovery with performance close to orthogonal PGD. We show experimentally, using two different deep projective priors (based on autoencoders and on denoising networks), that our stochastic orthogonal regularization yields projections that improve convergence speed and robustness of GPGD in challenging inverse problem settings, in accordance with our theoretical findings.

Parameter-free structure-texture image decomposition by unrolling

In this work, we propose a parameter-free and efficient method to tackle the structure-texture image decomposition problem. In particular, we present a neural network LPR-NET based on the unrolling of the Low Patch Rank model. On the one hand, this allows us to automatically learn parameters from data, and on the other hand to be computationally faster while obtaining qualitatively similar results compared to traditional iterative model-based methods. Moreover, despite being trained on synthetic images, numerical experiments show the ability of our network to generalize well when applied to natural images.

Towards optimal algorithms for the recovery of low-dimensional models with linear rates

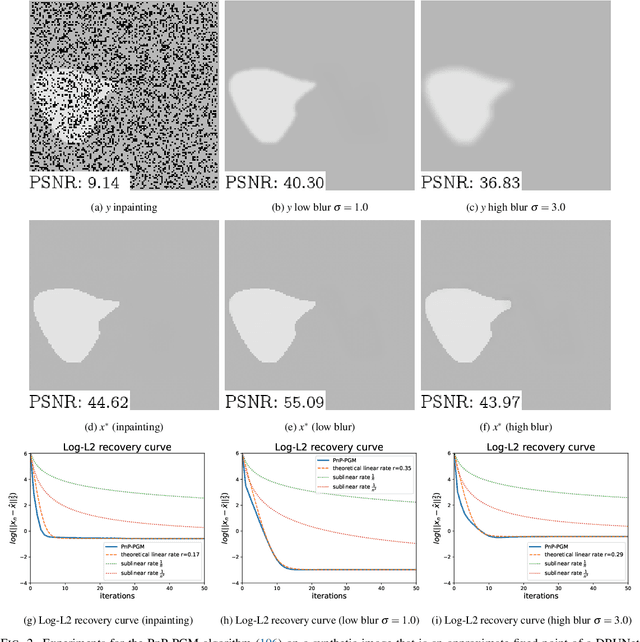
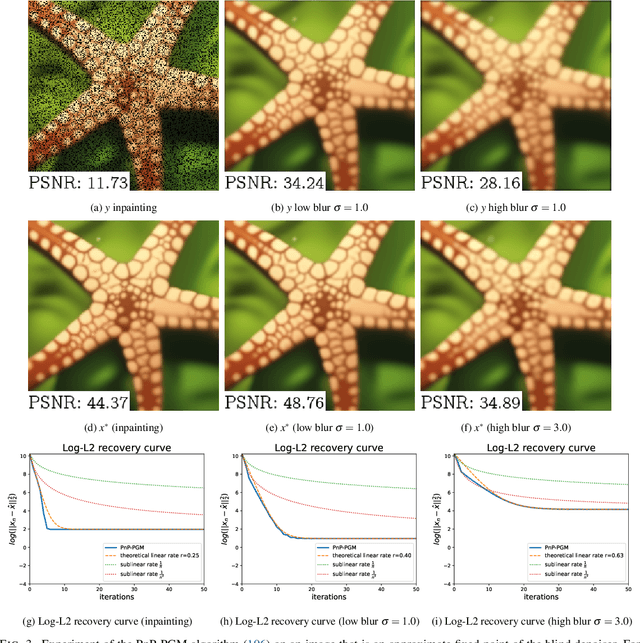
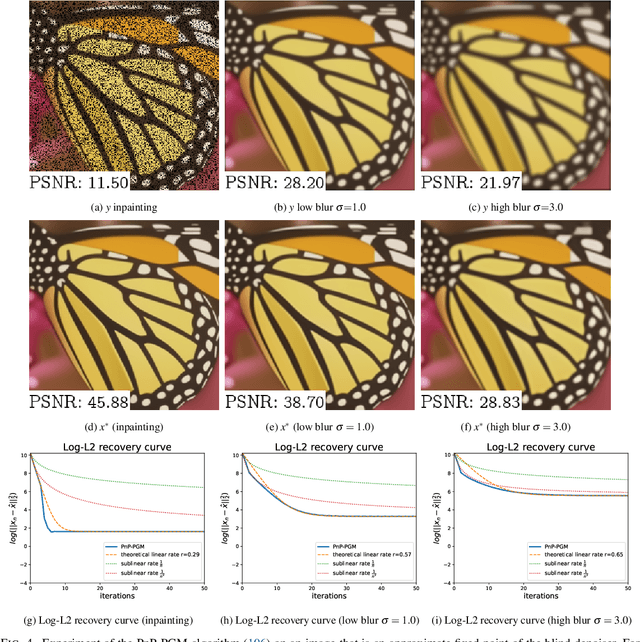
We consider the problem of recovering elements of a low-dimensional model from linear measurements. From signal and image processing to inverse problems in data science, this question has been at the center of many applications. Lately, with the success of models and methods relying on deep neural networks leading to non-convex formulations, traditional convex variational approaches have shown their limits. Furthermore, the multiplication of algorithms and recovery results makes identifying the best methods a complex task. In this article, we study recovery with a class of widely used algorithms without considering any underlying functional. This result leads to a class of projected gradient descent algorithms that recover a given low-dimensional with linear rates. The obtained rates decouple the impact of the quality of the measurements with respect to the model from its intrinsic complexity. As a consequence, we can directly measure the performance of this class of projected gradient descents through a restricted Lipschitz constant of the projection. By optimizing this constant, we define optimal algorithms. Our general approach provides an optimality result in the case of sparse recovery. Moreover, we uncover underlying linear rates of convergence for some ''plug and play'' imaging methods relying on deep priors by interpreting our results in this context, thus linking low-dimensional recovery and recovery with deep priors under a unified theory, validated by experiments on synthetic and real data.

Batch-less stochastic gradient descent for compressive learning of deep regularization for image denoising

We consider the problem of denoising with the help of prior information taken from a database of clean signals or images. Denoising with variational methods is very efficient if a regularizer well adapted to the nature of the data is available. Thanks to the maximum a posteriori Bayesian framework, such regularizer can be systematically linked with the distribution of the data. With deep neural networks (DNN), complex distributions can be recovered from a large training database.To reduce the computational burden of this task, we adapt the compressive learning framework to the learning of regularizers parametrized by DNN. We propose two variants of stochastic gradient descent (SGD) for the recovery of deep regularization parameters from a heavily compressed database. These algorithms outperform the initially proposed method that was limited to low-dimensional signals, each iteration using information from the whole database. They also benefit from classical SGD convergence guarantees. Thanks to these improvements we show that this method can be applied for patch based image denoising.}

Fast off-the-grid sparse recovery with over-parametrized projected gradient descent

We consider the problem of recovering off-the-grid spikes from Fourier measurements. Successful methods such as sliding Frank-Wolfe and continuous orthogonal matching pursuit (OMP) iteratively add spikes to the solution then perform a costly (when the number of spikes is large) descent on all parameters at each iteration. In 2D, it was shown that performing a projected gradient descent (PGD) from a gridded over-parametrized initialization was faster than continuous orthogonal matching pursuit. In this paper, we propose an off-the-grid over-parametrized initialization of the PGD based on OMP that permits to fully avoid grids and gives faster results in 3D.

A theory of optimal convex regularization for low-dimensional recovery

We consider the problem of recovering elements of a low-dimensional model from under-determined linear measurements. To perform recovery, we consider the minimization of a convex regularizer subject to a data fit constraint. Given a model, we ask ourselves what is the "best" convex regularizer to perform its recovery. To answer this question, we define an optimal regularizer as a function that maximizes a compliance measure with respect to the model. We introduce and study several notions of compliance. We give analytical expressions for compliance measures based on the best-known recovery guarantees with the restricted isometry property. These expressions permit to show the optimality of the {\ell} 1-norm for sparse recovery and of the nuclear norm for low-rank matrix recovery for these compliance measures. We also investigate the construction of an optimal convex regularizer using the example of sparsity in levels.

Statistical Learning Guarantees for Compressive Clustering and Compressive Mixture Modeling

We provide statistical learning guarantees for two unsupervised learning tasks in the context of compressive statistical learning, a general framework for resource-efficient large-scale learning that we introduced in a companion paper. The principle of compressive statistical learning is to compress a training collection, in one pass, into a low-dimensional sketch (a vector of random empirical generalized moments) that captures the information relevant to the considered learning task. We explicit random feature functions which empirical averages preserve the needed information for compressive clustering and compressive Gaussian mixture modeling with fixed known variance, and establish sufficient sketch sizes given the problem dimensions.

Compressive Statistical Learning with Random Feature Moments

We describe a general framework --compressive statistical learning-- for resource-efficient large-scale learning: the training collection is compressed in one pass into a low-dimensional sketch (a vector of random empirical generalized moments) that captures the information relevant to the considered learning task. A near-minimizer of the risk is computed from the sketch through the solution of a nonlinear least squares problem. We investigate sufficient sketch sizes to control the generalization error of this procedure. The framework is illustrated on compressive clustering, compressive Gaussian mixture Modeling with fixed known variance, and compressive PCA.

Phase Unmixing : Multichannel Source Separation with Magnitude Constraints

We consider the problem of estimating the phases of K mixed complex signals from a multichannel observation, when the mixing matrix and signal magnitudes are known. This problem can be cast as a non-convex quadratically constrained quadratic program which is known to be NP-hard in general. We propose three approaches to tackle it: a heuristic method, an alternate minimization method, and a convex relaxation into a semi-definite program. The last two approaches are showed to outperform the oracle multichannel Wiener filter in under-determined informed source separation tasks, using simulated and speech signals. The convex relaxation approach yields best results, including the potential for exact source separation in under-determined settings.