Variational Low-Rank Adaptation Using IVON

We show that variational learning can significantly improve the accuracy and calibration of Low-Rank Adaptation (LoRA) without a substantial increase in the cost. We replace AdamW by the Improved Variational Online Newton (IVON) algorithm to finetune large language models. For Llama-2 with 7 billion parameters, IVON improves the accuracy over AdamW by 2.8% and expected calibration error by 4.6%. The accuracy is also better than the other Bayesian alternatives, yet the cost is lower and the implementation is easier. Our work provides additional evidence for the effectiveness of IVON for large language models. The code is available at https://github.com/team-approx-bayes/ivon-lora.

Variational Learning is Effective for Large Deep Networks

We give extensive empirical evidence against the common belief that variational learning is ineffective for large neural networks. We show that an optimizer called Improved Variational Online Newton (IVON) consistently matches or outperforms Adam for training large networks such as GPT-2 and ResNets from scratch. IVON's computational costs are nearly identical to Adam but its predictive uncertainty is better. We show several new use cases of IVON where we improve fine-tuning and model merging in Large Language Models, accurately predict generalization error, and faithfully estimate sensitivity to data. We find overwhelming evidence in support of effectiveness of variational learning.

ResolvNet: A Graph Convolutional Network with multi-scale Consistency

It is by now a well known fact in the graph learning community that the presence of bottlenecks severely limits the ability of graph neural networks to propagate information over long distances. What so far has not been appreciated is that, counter-intuitively, also the presence of strongly connected sub-graphs may severely restrict information flow in common architectures. Motivated by this observation, we introduce the concept of multi-scale consistency. At the node level this concept refers to the retention of a connected propagation graph even if connectivity varies over a given graph. At the graph-level, multi-scale consistency refers to the fact that distinct graphs describing the same object at different resolutions should be assigned similar feature vectors. As we show, both properties are not satisfied by poular graph neural network architectures. To remedy these shortcomings, we introduce ResolvNet, a flexible graph neural network based on the mathematical concept of resolvents. We rigorously establish its multi-scale consistency theoretically and verify it in extensive experiments on real world data: Here networks based on this ResolvNet architecture prove expressive; out-performing baselines significantly on many tasks; in- and outside the multi-scale setting.

Beyond In-Domain Scenarios: Robust Density-Aware Calibration

Calibrating deep learning models to yield uncertainty-aware predictions is crucial as deep neural networks get increasingly deployed in safety-critical applications. While existing post-hoc calibration methods achieve impressive results on in-domain test datasets, they are limited by their inability to yield reliable uncertainty estimates in domain-shift and out-of-domain (OOD) scenarios. We aim to bridge this gap by proposing DAC, an accuracy-preserving as well as Density-Aware Calibration method based on k-nearest-neighbors (KNN). In contrast to existing post-hoc methods, we utilize hidden layers of classifiers as a source for uncertainty-related information and study their importance. We show that DAC is a generic method that can readily be combined with state-of-the-art post-hoc methods. DAC boosts the robustness of calibration performance in domain-shift and OOD, while maintaining excellent in-domain predictive uncertainty estimates. We demonstrate that DAC leads to consistently better calibration across a large number of model architectures, datasets, and metrics. Additionally, we show that DAC improves calibration substantially on recent large-scale neural networks pre-trained on vast amounts of data.

A Graph Is More Than Its Nodes: Towards Structured Uncertainty-Aware Learning on Graphs

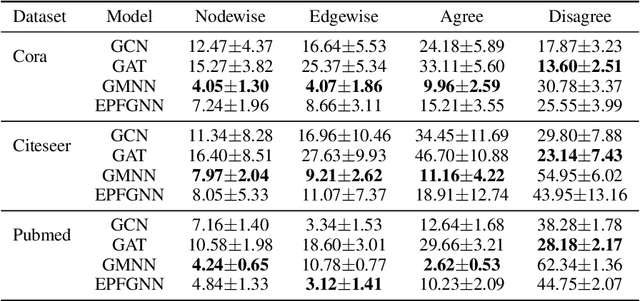
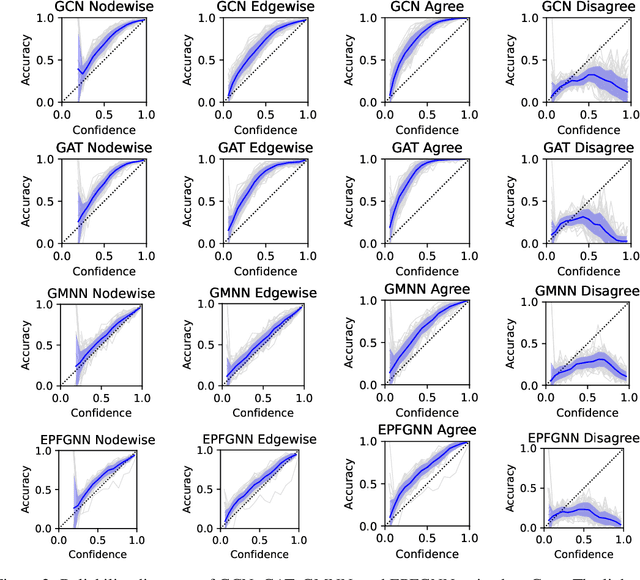
Current graph neural networks (GNNs) that tackle node classification on graphs tend to only focus on nodewise scores and are solely evaluated by nodewise metrics. This limits uncertainty estimation on graphs since nodewise marginals do not fully characterize the joint distribution given the graph structure. In this work, we propose novel edgewise metrics, namely the edgewise expected calibration error (ECE) and the agree/disagree ECEs, which provide criteria for uncertainty estimation on graphs beyond the nodewise setting. Our experiments demonstrate that the proposed edgewise metrics can complement the nodewise results and yield additional insights. Moreover, we show that GNN models which consider the structured prediction problem on graphs tend to have better uncertainty estimations, which illustrates the benefit of going beyond the nodewise setting.

Deep Combinatorial Aggregation

Neural networks are known to produce poor uncertainty estimations, and a variety of approaches have been proposed to remedy this issue. This includes deep ensemble, a simple and effective method that achieves state-of-the-art results for uncertainty-aware learning tasks. In this work, we explore a combinatorial generalization of deep ensemble called deep combinatorial aggregation (DCA). DCA creates multiple instances of network components and aggregates their combinations to produce diversified model proposals and predictions. DCA components can be defined at different levels of granularity. And we discovered that coarse-grain DCAs can outperform deep ensemble for uncertainty-aware learning both in terms of predictive performance and uncertainty estimation. For fine-grain DCAs, we discover that an average parameterization approach named deep combinatorial weight averaging (DCWA) can improve the baseline training. It is on par with stochastic weight averaging (SWA) but does not require any custom training schedule or adaptation of BatchNorm layers. Furthermore, we propose a consistency enforcing loss that helps the training of DCWA and modelwise DCA. We experiment on in-domain, distributional shift, and out-of-distribution image classification tasks, and empirically confirm the effectiveness of DCWA and DCA approaches.

What Makes Graph Neural Networks Miscalibrated?

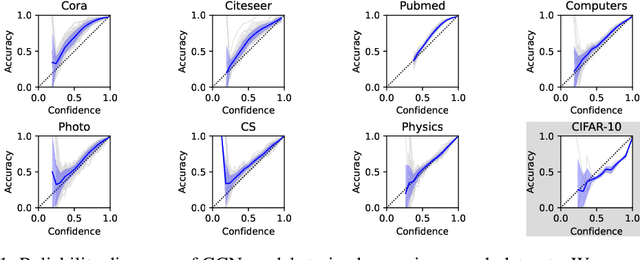
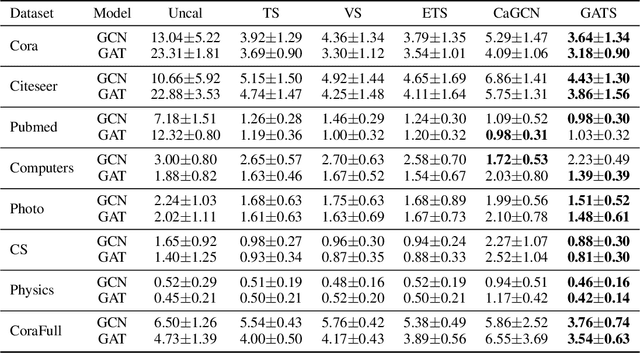
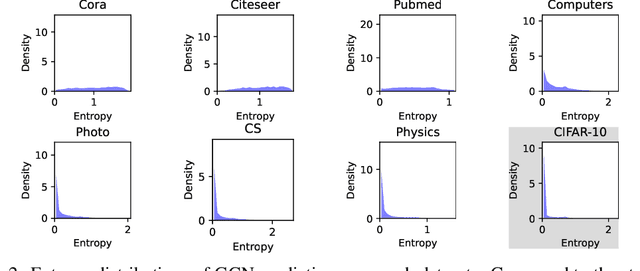
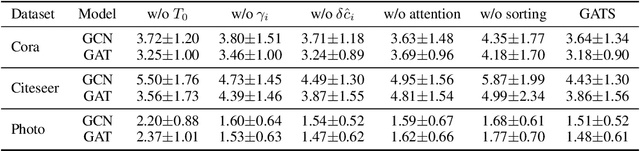
Given the importance of getting calibrated predictions and reliable uncertainty estimations, various post-hoc calibration methods have been developed for neural networks on standard multi-class classification tasks. However, these methods are not well suited for calibrating graph neural networks (GNNs), which presents unique challenges such as accounting for the graph structure and the graph-induced correlations between the nodes. In this work, we conduct a systematic study on the calibration qualities of GNN node predictions. In particular, we identify five factors which influence the calibration of GNNs: general under-confident tendency, diversity of nodewise predictive distributions, distance to training nodes, relative confidence level, and neighborhood similarity. Furthermore, based on the insights from this study, we design a novel calibration method named Graph Attention Temperature Scaling (GATS), which is tailored for calibrating graph neural networks. GATS incorporates designs that address all the identified influential factors and produces nodewise temperature scaling using an attention-based architecture. GATS is accuracy-preserving, data-efficient, and expressive at the same time. Our experiments empirically verify the effectiveness of GATS, demonstrating that it can consistently achieve state-of-the-art calibration results on various graph datasets for different GNN backbones.

Explicit Pairwise Factorized Graph Neural Network for Semi-Supervised Node Classification

Node features and structural information of a graph are both crucial for semi-supervised node classification problems. A variety of graph neural network (GNN) based approaches have been proposed to tackle these problems, which typically determine output labels through feature aggregation. This can be problematic, as it implies conditional independence of output nodes given hidden representations, despite their direct connections in the graph. To learn the direct influence among output nodes in a graph, we propose the Explicit Pairwise Factorized Graph Neural Network (EPFGNN), which models the whole graph as a partially observed Markov Random Field. It contains explicit pairwise factors to model output-output relations and uses a GNN backbone to model input-output relations. To balance model complexity and expressivity, the pairwise factors have a shared component and a separate scaling coefficient for each edge. We apply the EM algorithm to train our model, and utilize a star-shaped piecewise likelihood for the tractable surrogate objective. We conduct experiments on various datasets, which shows that our model can effectively improve the performance for semi-supervised node classification on graphs.

Deriving Neural Network Design and Learning from the Probabilistic Framework of Chain Graphs

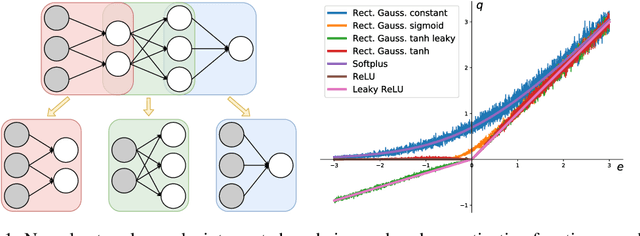
The last decade has witnessed a boom of neural network (NN) research and applications achieving state-of-the-art results in various domains. Yet, most advances on architecture and learning have been discovered empirically in a trial-and-error manner such that a more systematic exploration is difficult. Their theoretical analyses are limited and a unifying framework is absent. In this paper, we tackle this issue by identifying NNs as chain graphs (CGs) with chain components modeled as bipartite pairwise conditional random fields, and feed-forward as a form of approximate probabilistic inference. We show that from this CG interpretation we can systematically formulate an extensive range of the empirically discovered results, including various network designs (e.g., CNN, RNN, ResNet), activation functions (e.g., sigmoid, tanh, softmax, (leaky) ReLU) and regularizations (e.g., weight decay, dropout, BatchNorm). Furthermore, guided by this interpretation, we are able to derive "the preferred form" of residual block, recover the simple yet powerful IndRNN model and discover a new stochastic inference procedure: the partially collapsed feed-forward inference. We believe that our work can provide a well-founded formulation to analyze the nature and design of NNs, and can serve as a unifying theoretical framework for deep learning research.

Probabilistic Discriminative Learning with Layered Graphical Models

Probabilistic graphical models are traditionally known for their successes in generative modeling. In this work, we advocate layered graphical models (LGMs) for probabilistic discriminative learning. To this end, we design LGMs in close analogy to neural networks (NNs), that is, they have deep hierarchical structures and convolutional or local connections between layers. Equipped with tensorized truncated variational inference, our LGMs can be efficiently trained via backpropagation on mainstream deep learning frameworks such as PyTorch. To deal with continuous valued inputs, we use a simple yet effective soft-clamping strategy for efficient inference. Through extensive experiments on image classification over MNIST and FashionMNIST datasets, we demonstrate that LGMs are capable of achieving competitive results comparable to NNs of similar architectures, while preserving transparent probabilistic modeling.