Variational Learning is Effective for Large Deep Networks

We give extensive empirical evidence against the common belief that variational learning is ineffective for large neural networks. We show that an optimizer called Improved Variational Online Newton (IVON) consistently matches or outperforms Adam for training large networks such as GPT-2 and ResNets from scratch. IVON's computational costs are nearly identical to Adam but its predictive uncertainty is better. We show several new use cases of IVON where we improve fine-tuning and model merging in Large Language Models, accurately predict generalization error, and faithfully estimate sensitivity to data. We find overwhelming evidence in support of effectiveness of variational learning.

The Memory Perturbation Equation: Understanding Model's Sensitivity to Data

Understanding model's sensitivity to its training data is crucial but can also be challenging and costly, especially during training. To simplify such issues, we present the Memory-Perturbation Equation (MPE) which relates model's sensitivity to perturbation in its training data. Derived using Bayesian principles, the MPE unifies existing sensitivity measures, generalizes them to a wide-variety of models and algorithms, and unravels useful properties regarding sensitivities. Our empirical results show that sensitivity estimates obtained during training can be used to faithfully predict generalization on unseen test data. The proposed equation is expected to be useful for future research on robust and adaptive learning.

Variational Hierarchical Mixtures for Learning Probabilistic Inverse Dynamics

Well-calibrated probabilistic regression models are a crucial learning component in robotics applications as datasets grow rapidly and tasks become more complex. Classical regression models are usually either probabilistic kernel machines with a flexible structure that does not scale gracefully with data or deterministic and vastly scalable automata, albeit with a restrictive parametric form and poor regularization. In this paper, we consider a probabilistic hierarchical modeling paradigm that combines the benefits of both worlds to deliver computationally efficient representations with inherent complexity regularization. The presented approaches are probabilistic interpretations of local regression techniques that approximate nonlinear functions through a set of local linear or polynomial units. Importantly, we rely on principles from Bayesian nonparametrics to formulate flexible models that adapt their complexity to the data and can potentially encompass an infinite number of components. We derive two efficient variational inference techniques to learn these representations and highlight the advantages of hierarchical infinite local regression models, such as dealing with non-smooth functions, mitigating catastrophic forgetting, and enabling parameter sharing and fast predictions. Finally, we validate this approach on a set of large inverse dynamics datasets and test the learned models in real-world control scenarios.

A Variational Infinite Mixture for Probabilistic Inverse Dynamics Learning

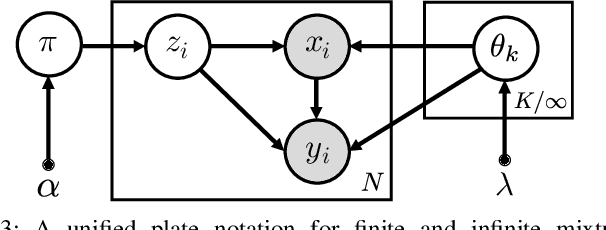
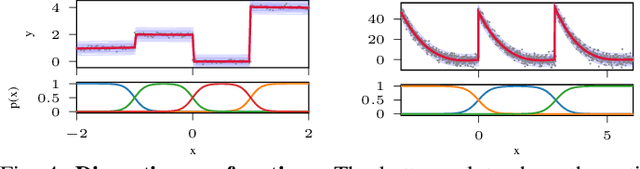
Probabilistic regression techniques in control and robotics applications have to fulfill different criteria of data-driven adaptability, computational efficiency, scalability to high dimensions, and the capacity to deal with different modalities in the data. Classical regressors usually fulfill only a subset of these properties. In this work, we extend seminal work on Bayesian nonparametric mixtures and derive an efficient variational Bayes inference technique for infinite mixtures of probabilistic local polynomial models with well-calibrated certainty quantification. We highlight the model's power in combining data-driven complexity adaptation, fast prediction and the ability to deal with discontinuous functions and heteroscedastic noise. We benchmark this technique on a range of large real inverse dynamics datasets, showing that the infinite mixture formulation is competitive with classical Local Learning methods and regularizes model complexity by adapting the number of components based on data and without relying on heuristics. Moreover, to showcase the practicality of the approach, we use the learned models for online inverse dynamics control of a Barret-WAM manipulator, significantly improving the trajectory tracking performance.