Variational Learning Induces Adaptive Label Smoothing

We show that variational learning naturally induces an adaptive label smoothing where label noise is specialized for each example. Such label-smoothing is useful to handle examples with labeling errors and distribution shifts, but designing a good adaptivity strategy is not always easy. We propose to skip this step and simply use the natural adaptivity induced during the optimization of a variational objective. We show empirical results where a variational algorithm called IVON outperforms traditional label smoothing and yields adaptivity strategies similar to those of an existing approach. By connecting Bayesian methods to label smoothing, our work provides a new way to handle overconfident predictions.

Variational Learning is Effective for Large Deep Networks

We give extensive empirical evidence against the common belief that variational learning is ineffective for large neural networks. We show that an optimizer called Improved Variational Online Newton (IVON) consistently matches or outperforms Adam for training large networks such as GPT-2 and ResNets from scratch. IVON's computational costs are nearly identical to Adam but its predictive uncertainty is better. We show several new use cases of IVON where we improve fine-tuning and model merging in Large Language Models, accurately predict generalization error, and faithfully estimate sensitivity to data. We find overwhelming evidence in support of effectiveness of variational learning.

Beyond Target Networks: Improving Deep $Q$-learning with Functional Regularization

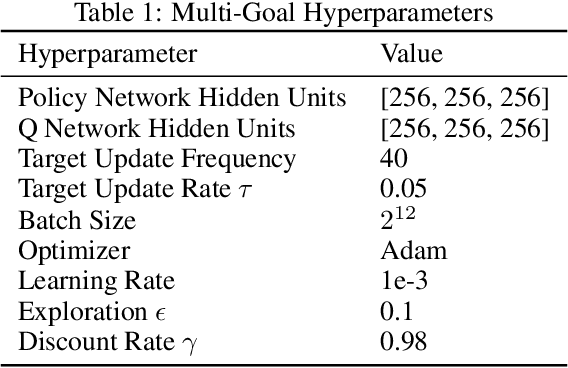
Target networks are at the core of recent success in Reinforcement Learning. They stabilize the training by using old parameters to estimate the $Q$-values, but this also limits the propagation of newly-encountered rewards which could ultimately slow down the training. In this work, we propose an alternative training method based on functional regularization which does not have this deficiency. Unlike target networks, our method uses up-to-date parameters to estimate the target $Q$-values, thereby speeding up training while maintaining stability. Surprisingly, in some cases, we can show that target networks are a special, restricted type of functional regularizers. Using this approach, we show empirical improvements in sample efficiency and performance across a range of Atari and simulated robotics environments.

Structured Prediction for CRiSP Inverse Kinematics Learning with Misspecified Robot Models

With the recent advances in machine learning, problems that traditionally would require accurate modeling to be solved analytically can now be successfully approached with data-driven strategies. Among these, computing the inverse kinematics of a redundant robot arm poses a significant challenge due to the non-linear structure of the robot, the hard joint constraints and the non-invertible kinematics map. Moreover, most learning algorithms consider a completely data-driven approach, while often useful information on the structure of the robot is available and should be positively exploited. In this work, we present a simple, yet effective, approach for learning the inverse kinematics. We introduce a structured prediction algorithm that combines a data-driven strategy with the model provided by a forward kinematics function -- even when this function is misspeficied -- to accurately solve the problem. The proposed approach ensures that predicted joint configurations are well within the robot's constraints. We also provide statistical guarantees on the generalization properties of our estimator as well as an empirical evaluation of its performance on trajectory reconstruction tasks.

Hyperbolic Manifold Regression

Geometric representation learning has recently shown great promise in several machine learning settings, ranging from relational learning to language processing and generative models. In this work, we consider the problem of performing manifold-valued regression onto an hyperbolic space as an intermediate component for a number of relevant machine learning applications. In particular, by formulating the problem of predicting nodes of a tree as a manifold regression task in the hyperbolic space, we propose a novel perspective on two challenging tasks: 1) hierarchical classification via label embeddings and 2) taxonomy extension of hyperbolic representations. To address the regression problem we consider previous methods as well as proposing two novel approaches that are computationally more advantageous: a parametric deep learning model that is informed by the geodesics of the target space and a non-parametric kernel-method for which we also prove excess risk bounds. Our experiments show that the strategy of leveraging the hyperbolic geometry is promising. In particular, in the taxonomy expansion setting, we find that the hyperbolic-based estimators significantly outperform methods performing regression in the ambient Euclidean space.

Manifold Structured Prediction

Structured prediction provides a general framework to deal with supervised problems where the outputs have semantically rich structure. While classical approaches consider finite, albeit potentially huge, output spaces, in this paper we discuss how structured prediction can be extended to a continuous scenario. Specifically, we study a structured prediction approach to manifold valued regression. We characterize a class of problems for which the considered approach is statistically consistent and study how geometric optimization can be used to compute the corresponding estimator. Promising experimental results on both simulated and real data complete our study.