Sequential Monte Carlo for Policy Optimization in Continuous POMDPs

Optimal decision-making under partial observability requires agents to balance reducing uncertainty (exploration) against pursuing immediate objectives (exploitation). In this paper, we introduce a novel policy optimization framework for continuous partially observable Markov decision processes (POMDPs) that explicitly addresses this challenge. Our method casts policy learning as probabilistic inference in a non-Markovian Feynman--Kac model that inherently captures the value of information gathering by anticipating future observations, without requiring extrinsic exploration bonuses or handcrafted heuristics. To optimize policies under this model, we develop a nested sequential Monte Carlo~(SMC) algorithm that efficiently estimates a history-dependent policy gradient under samples from the optimal trajectory distribution induced by the POMDP. We demonstrate the effectiveness of our algorithm across standard continuous POMDP benchmarks, where existing methods struggle to act under uncertainty.

A Parallel-in-Time Newton's Method for Nonlinear Model Predictive Control

Model predictive control (MPC) is a powerful framework for optimal control of dynamical systems. However, MPC solvers suffer from a high computational burden that restricts their application to systems with low sampling frequency. This issue is further amplified in nonlinear and constrained systems that require nesting MPC solvers within iterative procedures. In this paper, we address these issues by developing parallel-in-time algorithms for constrained nonlinear optimization problems that take advantage of massively parallel hardware to achieve logarithmic computational time scaling over the planning horizon. We develop time-parallel second-order solvers based on interior point methods and the alternating direction method of multipliers, leveraging fast convergence and lower computational cost per iteration. The parallelization is based on a reformulation of the subproblems in terms of associative operations that can be parallelized using the associative scan algorithm. We validate our approach on numerical examples of nonlinear and constrained dynamical systems.

Recursive Nested Filtering for Efficient Amortized Bayesian Experimental Design

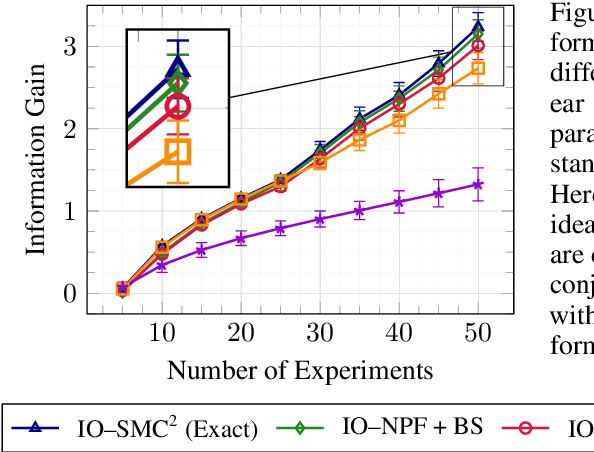
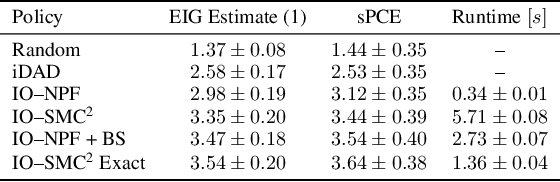
This paper introduces the Inside-Out Nested Particle Filter (IO-NPF), a novel, fully recursive, algorithm for amortized sequential Bayesian experimental design in the non-exchangeable setting. We frame policy optimization as maximum likelihood estimation in a non-Markovian state-space model, achieving (at most) $\mathcal{O}(T^2)$ computational complexity in the number of experiments. We provide theoretical convergence guarantees and introduce a backward sampling algorithm to reduce trajectory degeneracy. IO-NPF offers a practical, extensible, and provably consistent approach to sequential Bayesian experimental design, demonstrating improved efficiency over existing methods.

Nesting Particle Filters for Experimental Design in Dynamical Systems

In this paper, we propose a novel approach to Bayesian Experimental Design (BED) for non-exchangeable data that formulates it as risk-sensitive policy optimization. We develop the Inside-Out SMC^2 algorithm that uses a nested sequential Monte Carlo (SMC) estimator of the expected information gain and embeds it into a particle Markov chain Monte Carlo (pMCMC) framework to perform gradient-based policy optimization. This is in contrast to recent approaches that rely on biased estimators of the expected information gain (EIG) to amortize the cost of experiments by learning a design policy in advance. Numerical validation on a set of dynamical systems showcases the efficacy of our method in comparison to other state-of-the-art strategies.

Risk-Sensitive Stochastic Optimal Control as Rao-Blackwellized Markovian Score Climbing

Stochastic optimal control of dynamical systems is a crucial challenge in sequential decision-making. Recently, control-as-inference approaches have had considerable success, providing a viable risk-sensitive framework to address the exploration-exploitation dilemma. Nonetheless, a majority of these techniques only invoke the inference-control duality to derive a modified risk objective that is then addressed within a reinforcement learning framework. This paper introduces a novel perspective by framing risk-sensitive stochastic control as Markovian score climbing under samples drawn from a conditional particle filter. Our approach, while purely inference-centric, provides asymptotically unbiased estimates for gradient-based policy optimization with optimal importance weighting and no explicit value function learning. To validate our methodology, we apply it to the task of learning neural non-Gaussian feedback policies, showcasing its efficacy on numerical benchmarks of stochastic dynamical systems.

A Recursive Newton Method for Smoothing in Nonlinear State Space Models

In this paper, we use the optimization formulation of nonlinear Kalman filtering and smoothing problems to develop second-order variants of iterated Kalman smoother (IKS) methods. We show that Newton's method corresponds to a recursion over affine smoothing problems on a modified state-space model augmented by a pseudo measurement. The first and second derivatives required in this approach can be efficiently computed with widely available automatic differentiation tools. Furthermore, we show how to incorporate line-search and trust-region strategies into the proposed second-order IKS algorithm in order to regularize updates between iterations. Finally, we provide numerical examples to demonstrate the method's efficiency in terms of runtime compared to its batch counterpart.

Variational Gaussian filtering via Wasserstein gradient flows

In this article, we present a variational approach to Gaussian and mixture-of-Gaussians assumed filtering. Our method relies on an approximation stemming from the gradient-flow representations of a Kullback--Leibler discrepancy minimization. We outline the general method and show its competitiveness in parameter estimation and posterior representation for two models for which Gaussian approximations typically fail: a multiplicative noise and a multi-modal model.

Variational Hierarchical Mixtures for Learning Probabilistic Inverse Dynamics

Well-calibrated probabilistic regression models are a crucial learning component in robotics applications as datasets grow rapidly and tasks become more complex. Classical regression models are usually either probabilistic kernel machines with a flexible structure that does not scale gracefully with data or deterministic and vastly scalable automata, albeit with a restrictive parametric form and poor regularization. In this paper, we consider a probabilistic hierarchical modeling paradigm that combines the benefits of both worlds to deliver computationally efficient representations with inherent complexity regularization. The presented approaches are probabilistic interpretations of local regression techniques that approximate nonlinear functions through a set of local linear or polynomial units. Importantly, we rely on principles from Bayesian nonparametrics to formulate flexible models that adapt their complexity to the data and can potentially encompass an infinite number of components. We derive two efficient variational inference techniques to learn these representations and highlight the advantages of hierarchical infinite local regression models, such as dealing with non-smooth functions, mitigating catastrophic forgetting, and enabling parameter sharing and fast predictions. Finally, we validate this approach on a set of large inverse dynamics datasets and test the learned models in real-world control scenarios.

Model-Based Reinforcement Learning for Stochastic Hybrid Systems

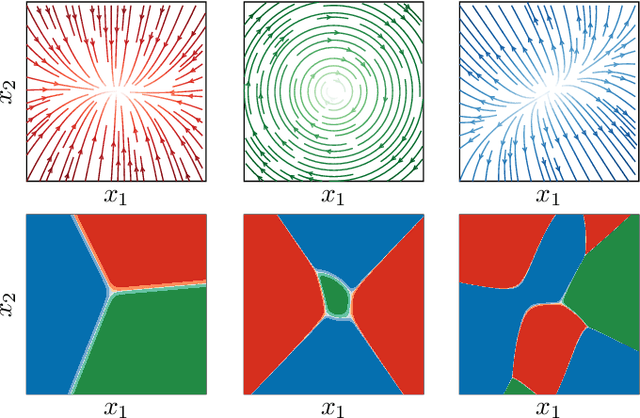
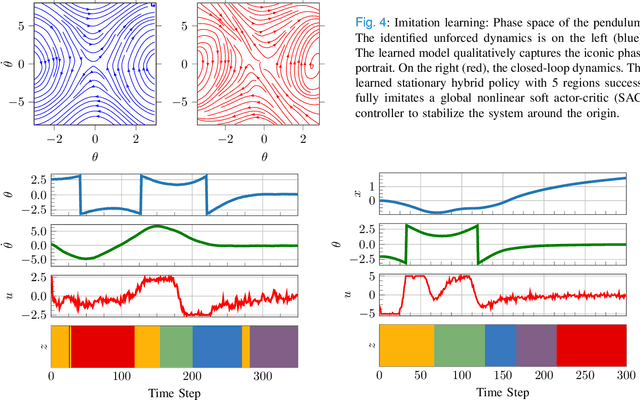
Optimal control of general nonlinear systems is a central challenge in automation. Data-driven approaches to control, enabled by powerful function approximators, have recently had great success in tackling challenging robotic applications. However, such methods often obscure the structure of dynamics and control behind black-box over-parameterized representations, thus limiting our ability to understand the closed-loop behavior. This paper adopts a hybrid-system view of nonlinear modeling and control that lends an explicit hierarchical structure to the problem and breaks down complex dynamics into simpler localized units. Therefore, we consider a sequence modeling paradigm that captures the temporal structure of the data and derive an expecation-maximization (EM) algorithm that automatically decomposes nonlinear dynamics into stochastic piecewise affine dynamical systems with nonlinear boundaries. Furthermore, we show that these time-series models naturally admit a closed-loop extension that we use to extract locally linear or polynomial feedback controllers from nonlinear experts via imitation learning. Finally, we introduce a novel hybrid realtive entropy policy search (Hb-REPS) technique that incorporates the hierarchical nature of hybrid systems and optimizes a set of time-invariant local feedback controllers derived from a locally polynomial approximation of a global value function.

Stochastic Control through Approximate Bayesian Input Inference

Optimal control under uncertainty is a prevailing challenge in control, due to the difficulty in producing tractable solutions for the stochastic optimization problem. By framing the control problem as one of input estimation, advanced approximate inference techniques can be used to handle the statistical approximations in a principled and practical manner. Analyzing the Gaussian setting, we present a solver capable of several stochastic control methods, and was found to be superior to popular baselines on nonlinear simulated tasks. We draw connections that relate this inference formulation to previous approaches for stochastic optimal control, and outline several advantages that this inference view brings due to its statistical nature.