Sequential Monte Carlo for Policy Optimization in Continuous POMDPs

Optimal decision-making under partial observability requires agents to balance reducing uncertainty (exploration) against pursuing immediate objectives (exploitation). In this paper, we introduce a novel policy optimization framework for continuous partially observable Markov decision processes (POMDPs) that explicitly addresses this challenge. Our method casts policy learning as probabilistic inference in a non-Markovian Feynman--Kac model that inherently captures the value of information gathering by anticipating future observations, without requiring extrinsic exploration bonuses or handcrafted heuristics. To optimize policies under this model, we develop a nested sequential Monte Carlo~(SMC) algorithm that efficiently estimates a history-dependent policy gradient under samples from the optimal trajectory distribution induced by the POMDP. We demonstrate the effectiveness of our algorithm across standard continuous POMDP benchmarks, where existing methods struggle to act under uncertainty.

Recursive Nested Filtering for Efficient Amortized Bayesian Experimental Design

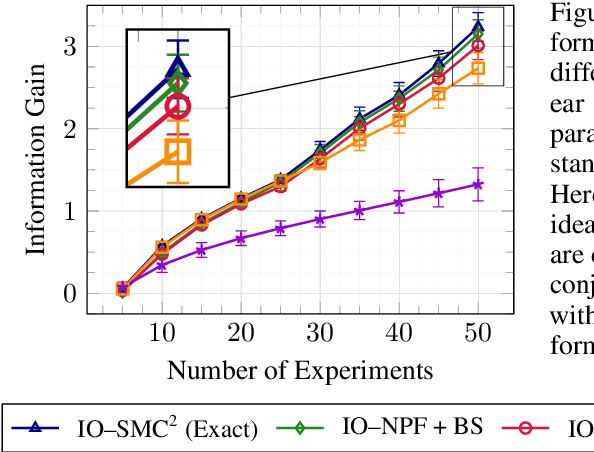
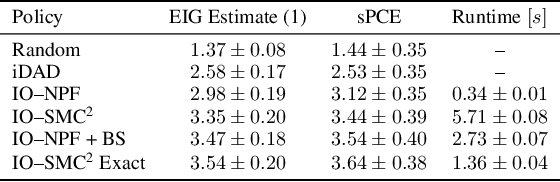
This paper introduces the Inside-Out Nested Particle Filter (IO-NPF), a novel, fully recursive, algorithm for amortized sequential Bayesian experimental design in the non-exchangeable setting. We frame policy optimization as maximum likelihood estimation in a non-Markovian state-space model, achieving (at most) $\mathcal{O}(T^2)$ computational complexity in the number of experiments. We provide theoretical convergence guarantees and introduce a backward sampling algorithm to reduce trajectory degeneracy. IO-NPF offers a practical, extensible, and provably consistent approach to sequential Bayesian experimental design, demonstrating improved efficiency over existing methods.

Nesting Particle Filters for Experimental Design in Dynamical Systems

In this paper, we propose a novel approach to Bayesian Experimental Design (BED) for non-exchangeable data that formulates it as risk-sensitive policy optimization. We develop the Inside-Out SMC^2 algorithm that uses a nested sequential Monte Carlo (SMC) estimator of the expected information gain and embeds it into a particle Markov chain Monte Carlo (pMCMC) framework to perform gradient-based policy optimization. This is in contrast to recent approaches that rely on biased estimators of the expected information gain (EIG) to amortize the cost of experiments by learning a design policy in advance. Numerical validation on a set of dynamical systems showcases the efficacy of our method in comparison to other state-of-the-art strategies.

Risk-Sensitive Stochastic Optimal Control as Rao-Blackwellized Markovian Score Climbing

Stochastic optimal control of dynamical systems is a crucial challenge in sequential decision-making. Recently, control-as-inference approaches have had considerable success, providing a viable risk-sensitive framework to address the exploration-exploitation dilemma. Nonetheless, a majority of these techniques only invoke the inference-control duality to derive a modified risk objective that is then addressed within a reinforcement learning framework. This paper introduces a novel perspective by framing risk-sensitive stochastic control as Markovian score climbing under samples drawn from a conditional particle filter. Our approach, while purely inference-centric, provides asymptotically unbiased estimates for gradient-based policy optimization with optimal importance weighting and no explicit value function learning. To validate our methodology, we apply it to the task of learning neural non-Gaussian feedback policies, showcasing its efficacy on numerical benchmarks of stochastic dynamical systems.