Model-Based Reinforcement Learning for Stochastic Hybrid Systems
Paper and Code
Nov 11, 2021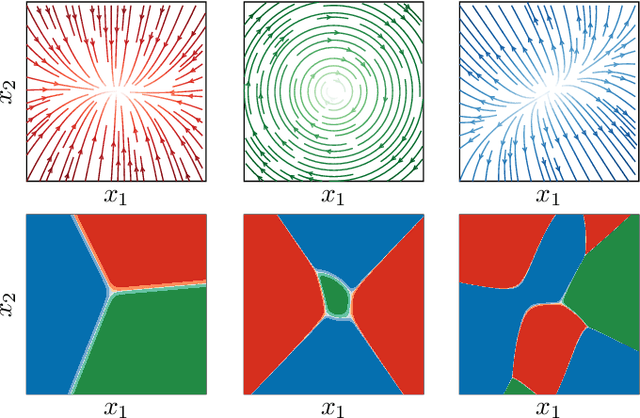


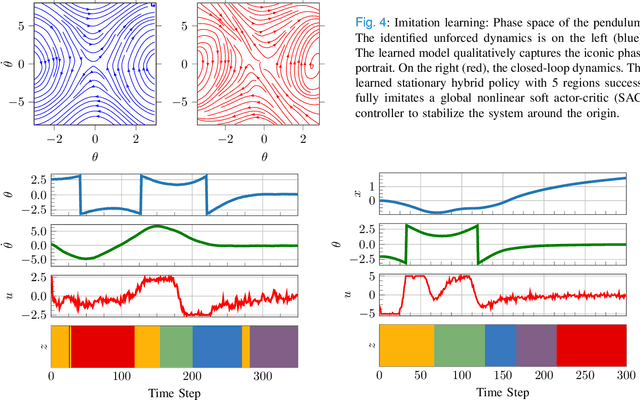
Optimal control of general nonlinear systems is a central challenge in automation. Data-driven approaches to control, enabled by powerful function approximators, have recently had great success in tackling challenging robotic applications. However, such methods often obscure the structure of dynamics and control behind black-box over-parameterized representations, thus limiting our ability to understand the closed-loop behavior. This paper adopts a hybrid-system view of nonlinear modeling and control that lends an explicit hierarchical structure to the problem and breaks down complex dynamics into simpler localized units. Therefore, we consider a sequence modeling paradigm that captures the temporal structure of the data and derive an expecation-maximization (EM) algorithm that automatically decomposes nonlinear dynamics into stochastic piecewise affine dynamical systems with nonlinear boundaries. Furthermore, we show that these time-series models naturally admit a closed-loop extension that we use to extract locally linear or polynomial feedback controllers from nonlinear experts via imitation learning. Finally, we introduce a novel hybrid realtive entropy policy search (Hb-REPS) technique that incorporates the hierarchical nature of hybrid systems and optimizes a set of time-invariant local feedback controllers derived from a locally polynomial approximation of a global value function.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge