A Variational Infinite Mixture for Probabilistic Inverse Dynamics Learning

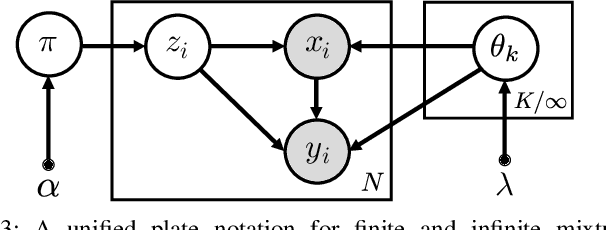
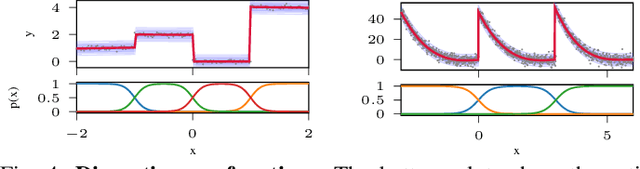
Probabilistic regression techniques in control and robotics applications have to fulfill different criteria of data-driven adaptability, computational efficiency, scalability to high dimensions, and the capacity to deal with different modalities in the data. Classical regressors usually fulfill only a subset of these properties. In this work, we extend seminal work on Bayesian nonparametric mixtures and derive an efficient variational Bayes inference technique for infinite mixtures of probabilistic local polynomial models with well-calibrated certainty quantification. We highlight the model's power in combining data-driven complexity adaptation, fast prediction and the ability to deal with discontinuous functions and heteroscedastic noise. We benchmark this technique on a range of large real inverse dynamics datasets, showing that the infinite mixture formulation is competitive with classical Local Learning methods and regularizes model complexity by adapting the number of components based on data and without relying on heuristics. Moreover, to showcase the practicality of the approach, we use the learned models for online inverse dynamics control of a Barret-WAM manipulator, significantly improving the trajectory tracking performance.