Quantifying Epistemic Uncertainty in Absolute Pose Regression

Visual relocalization is the task of estimating the camera pose given an image it views. Absolute pose regression offers a solution to this task by training a neural network, directly regressing the camera pose from image features. While an attractive solution in terms of memory and compute efficiency, absolute pose regression's predictions are inaccurate and unreliable outside the training domain. In this work, we propose a novel method for quantifying the epistemic uncertainty of an absolute pose regression model by estimating the likelihood of observations within a variational framework. Beyond providing a measure of confidence in predictions, our approach offers a unified model that also handles observation ambiguities, probabilistically localizing the camera in the presence of repetitive structures. Our method outperforms existing approaches in capturing the relation between uncertainty and prediction error.

Conditional Variational Autoencoders for Probabilistic Pose Regression

Robots rely on visual relocalization to estimate their pose from camera images when they lose track. One of the challenges in visual relocalization is repetitive structures in the operation environment of the robot. This calls for probabilistic methods that support multiple hypotheses for robot's pose. We propose such a probabilistic method to predict the posterior distribution of camera poses given an observed image. Our proposed training strategy results in a generative model of camera poses given an image, which can be used to draw samples from the pose posterior distribution. Our method is streamlined and well-founded in theory and outperforms existing methods on localization in presence of ambiguities.

A Probabilistic Framework for Visual Localization in Ambiguous Scenes

Visual localization allows autonomous robots to relocalize when losing track of their pose by matching their current observation with past ones. However, ambiguous scenes pose a challenge for such systems, as repetitive structures can be viewed from many distinct, equally likely camera poses, which means it is not sufficient to produce a single best pose hypothesis. In this work, we propose a probabilistic framework that for a given image predicts the arbitrarily shaped posterior distribution of its camera pose. We do this via a novel formulation of camera pose regression using variational inference, which allows sampling from the predicted distribution. Our method outperforms existing methods on localization in ambiguous scenes. Code and data will be released at https://github.com/efreidun/vapor.

Semi-supervised Learning of Partial Differential Operators and Dynamical Flows

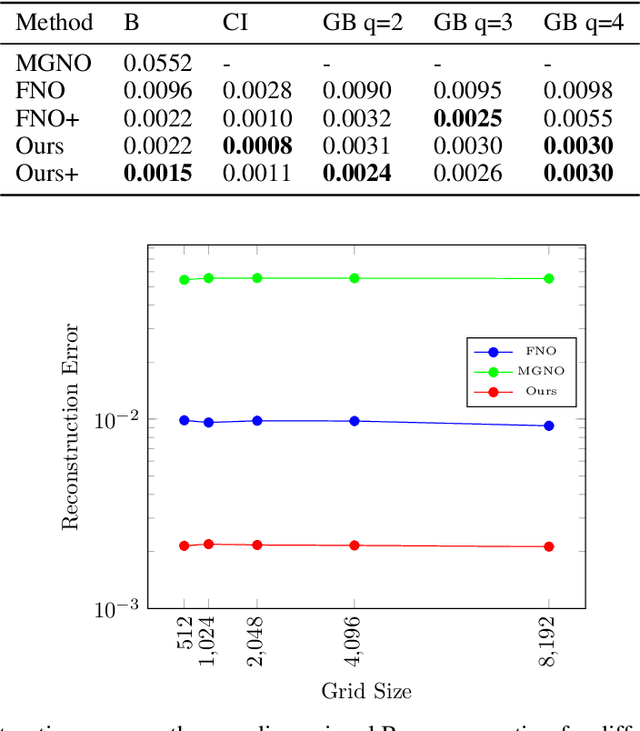
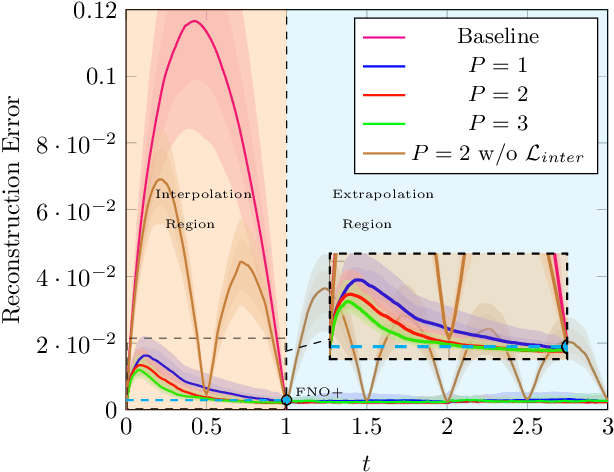
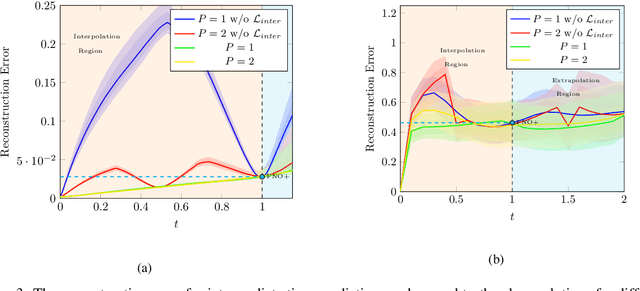
The evolution of dynamical systems is generically governed by nonlinear partial differential equations (PDEs), whose solution, in a simulation framework, requires vast amounts of computational resources. In this work, we present a novel method that combines a hyper-network solver with a Fourier Neural Operator architecture. Our method treats time and space separately. As a result, it successfully propagates initial conditions in continuous time steps by employing the general composition properties of the partial differential operators. Following previous work, supervision is provided at a specific time point. We test our method on various time evolution PDEs, including nonlinear fluid flows in one, two, and three spatial dimensions. The results show that the new method improves the learning accuracy at the time point of supervision point, and is able to interpolate and the solutions to any intermediate time.

Unsupervised Disentanglement with Tensor Product Representations on the Torus

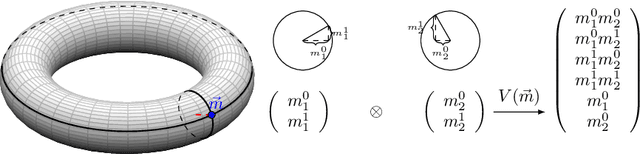
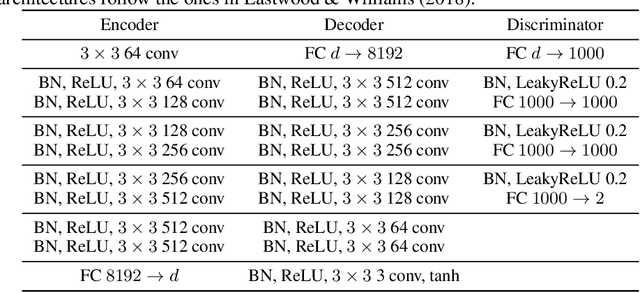
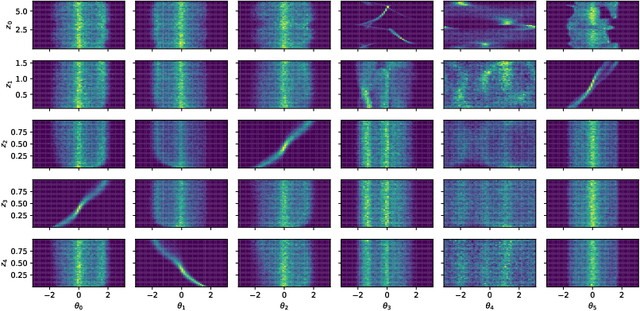
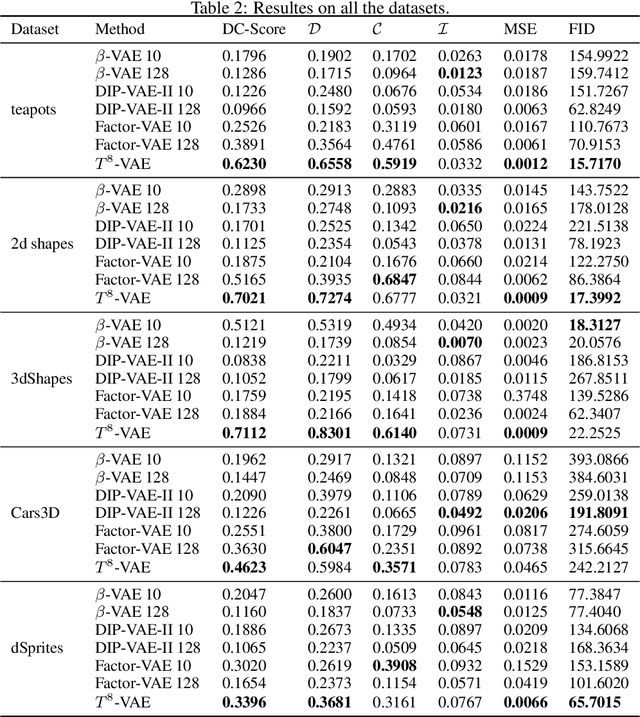
The current methods for learning representations with auto-encoders almost exclusively employ vectors as the latent representations. In this work, we propose to employ a tensor product structure for this purpose. This way, the obtained representations are naturally disentangled. In contrast to the conventional variations methods, which are targeted toward normally distributed features, the latent space in our representation is distributed uniformly over a set of unit circles. We argue that the torus structure of the latent space captures the generative factors effectively. We employ recent tools for measuring unsupervised disentanglement, and in an extensive set of experiments demonstrate the advantage of our method in terms of disentanglement, completeness, and informativeness. The code for our proposed method is available at https://github.com/rotmanmi/Unsupervised-Disentanglement-Torus.

Optimal least-squares solution to the hand-eye calibration problem

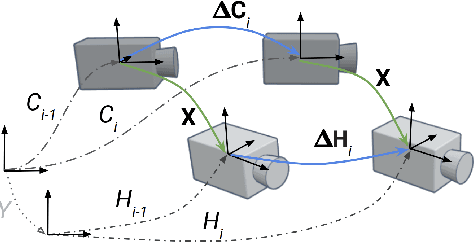
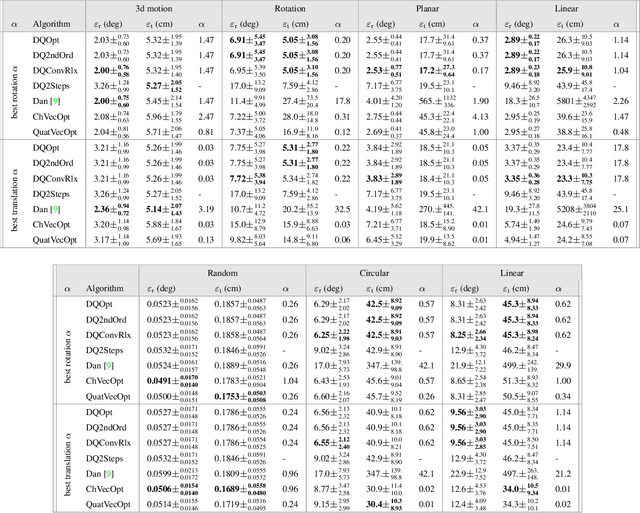
We propose a least-squares formulation to the noisy hand-eye calibration problem using dual-quaternions, and introduce efficient algorithms to find the exact optimal solution, based on analytic properties of the problem, avoiding non-linear optimization. We further present simple analytic approximate solutions which provide remarkably good estimations compared to the exact solution. In addition, we show how to generalize our solution to account for a given extrinsic prior in the cost function. To the best of our knowledge our algorithm is the most efficient approach to optimally solve the hand-eye calibration problem.