Input Space Mode Connectivity in Deep Neural Networks

We extend the concept of loss landscape mode connectivity to the input space of deep neural networks. Mode connectivity was originally studied within parameter space, where it describes the existence of low-loss paths between different solutions (loss minimizers) obtained through gradient descent. We present theoretical and empirical evidence of its presence in the input space of deep networks, thereby highlighting the broader nature of the phenomenon. We observe that different input images with similar predictions are generally connected, and for trained models, the path tends to be simple, with only a small deviation from being a linear path. Our methodology utilizes real, interpolated, and synthetic inputs created using the input optimization technique for feature visualization. We conjecture that input space mode connectivity in high-dimensional spaces is a geometric effect that takes place even in untrained models and can be explained through percolation theory. We exploit mode connectivity to obtain new insights about adversarial examples and demonstrate its potential for adversarial detection. Additionally, we discuss applications for the interpretability of deep networks.

Classifying Overlapping Gaussian Mixtures in High Dimensions: From Optimal Classifiers to Neural Nets

We derive closed-form expressions for the Bayes optimal decision boundaries in binary classification of high dimensional overlapping Gaussian mixture model (GMM) data, and show how they depend on the eigenstructure of the class covariances, for particularly interesting structured data. We empirically demonstrate, through experiments on synthetic GMMs inspired by real-world data, that deep neural networks trained for classification, learn predictors which approximate the derived optimal classifiers. We further extend our study to networks trained on authentic data, observing that decision thresholds correlate with the covariance eigenvectors rather than the eigenvalues, mirroring our GMM analysis. This provides theoretical insights regarding neural networks' ability to perform probabilistic inference and distill statistical patterns from intricate distributions.

Weak Correlations as the Underlying Principle for Linearization of Gradient-Based Learning Systems

Deep learning models, such as wide neural networks, can be conceptualized as nonlinear dynamical physical systems characterized by a multitude of interacting degrees of freedom. Such systems in the infinite limit, tend to exhibit simplified dynamics. This paper delves into gradient descent-based learning algorithms, that display a linear structure in their parameter dynamics, reminiscent of the neural tangent kernel. We establish this apparent linearity arises due to weak correlations between the first and higher-order derivatives of the hypothesis function, concerning the parameters, taken around their initial values. This insight suggests that these weak correlations could be the underlying reason for the observed linearization in such systems. As a case in point, we showcase this weak correlations structure within neural networks in the large width limit. Exploiting the relationship between linearity and weak correlations, we derive a bound on deviations from linearity observed during the training trajectory of stochastic gradient descent. To facilitate our proof, we introduce a novel method to characterise the asymptotic behavior of random tensors.

Turbulence Scaling from Deep Learning Diffusion Generative Models

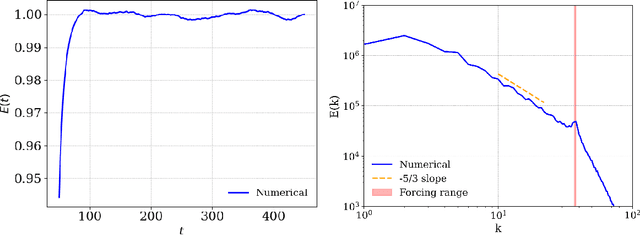
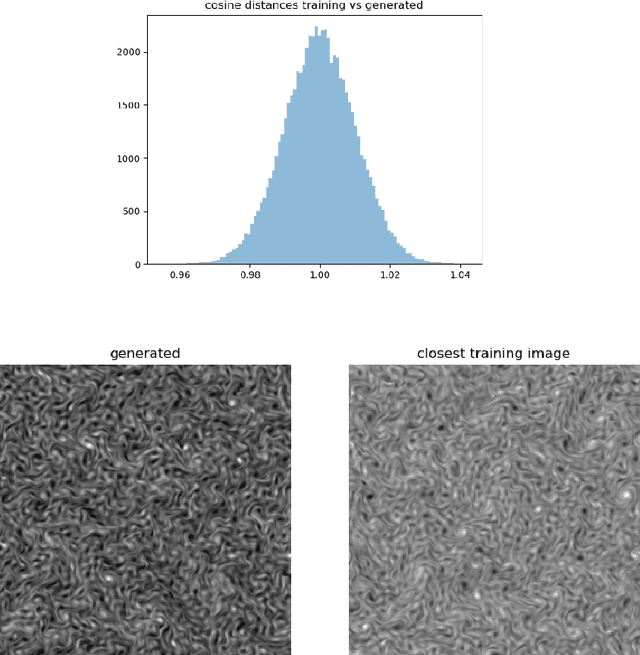
Complex spatial and temporal structures are inherent characteristics of turbulent fluid flows and comprehending them poses a major challenge. This comprehesion necessitates an understanding of the space of turbulent fluid flow configurations. We employ a diffusion-based generative model to learn the distribution of turbulent vorticity profiles and generate snapshots of turbulent solutions to the incompressible Navier-Stokes equations. We consider the inverse cascade in two spatial dimensions and generate diverse turbulent solutions that differ from those in the training dataset. We analyze the statistical scaling properties of the new turbulent profiles, calculate their structure functions, energy power spectrum, velocity probability distribution function and moments of local energy dissipation. All the learnt scaling exponents are consistent with the expected Kolmogorov scaling and have lower errors than the training ones. This agreement with established turbulence characteristics provides strong evidence of the model's capability to capture essential features of real-world turbulence.

The Universal Statistical Structure and Scaling Laws of Chaos and Turbulence

Turbulence is a complex spatial and temporal structure created by the strong non-linear dynamics of fluid flows at high Reynolds numbers. Despite being an ubiquitous phenomenon that has been studied for centuries, a full understanding of turbulence remained a formidable challenge. Here, we introduce tools from the fields of quantum chaos and Random Matrix Theory (RMT) and present a detailed analysis of image datasets generated from turbulence simulations of incompressible and compressible fluid flows. Focusing on two observables: the data Gram matrix and the single image distribution, we study both the local and global eigenvalue statistics and compare them to classical chaos, uncorrelated noise and natural images. We show that from the RMT perspective, the turbulence Gram matrices lie in the same universality class as quantum chaotic rather than integrable systems, and the data exhibits power-law scalings in the bulk of its eigenvalues which are vastly different from uncorrelated classical chaos, random data, natural images. Interestingly, we find that the single sample distribution only appears as fully RMT chaotic, but deviates from chaos at larger correlation lengths, as well as exhibiting different scaling properties.

The Underlying Scaling Laws and Universal Statistical Structure of Complex Datasets

We study universal traits which emerge both in real-world complex datasets, as well as in artificially generated ones. Our approach is to analogize data to a physical system and employ tools from statistical physics and Random Matrix Theory (RMT) to reveal their underlying structure. We focus on the feature-feature covariance matrix, analyzing both its local and global eigenvalue statistics. Our main observations are: (i) The power-law scalings that the bulk of its eigenvalues exhibit are vastly different for uncorrelated random data compared to real-world data, (ii) this scaling behavior can be completely recovered by introducing long range correlations in a simple way to the synthetic data, (iii) both generated and real-world datasets lie in the same universality class from the RMT perspective, as chaotic rather than integrable systems, (iv) the expected RMT statistical behavior already manifests for empirical covariance matrices at dataset sizes significantly smaller than those conventionally used for real-world training, and can be related to the number of samples required to approximate the population power-law scaling behavior, (v) the Shannon entropy is correlated with local RMT structure and eigenvalues scaling, and substantially smaller in strongly correlated datasets compared to uncorrelated synthetic data, and requires fewer samples to reach the distribution entropy. These findings can have numerous implications to the characterization of the complexity of data sets, including differentiating synthetically generated from natural data, quantifying noise, developing better data pruning methods and classifying effective learning models utilizing these scaling laws.

Neural Network Complexity of Chaos and Turbulence

We study the complexity of chaos and turbulence as viewed by deep neural networks by considering network classification tasks of distinguishing turbulent from chaotic fluid flows, noise and real world images of cats or dogs. We analyze the relative difficulty of these classification tasks and quantify the complexity of the computation at the intermediate and final stages. We analyze incompressible as well as weakly compressible fluid flows and provide evidence for the feature identified by the neural network to distinguish turbulence from chaos.

Semi-supervised Learning of Partial Differential Operators and Dynamical Flows

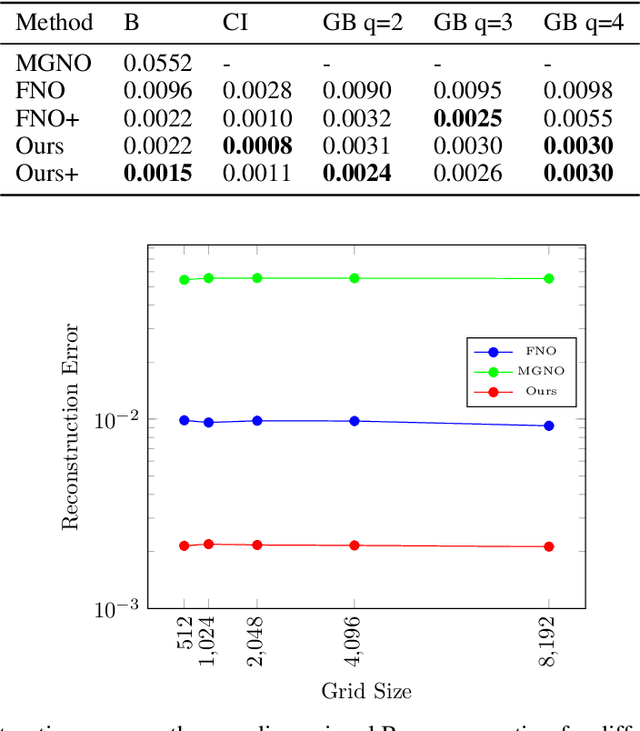
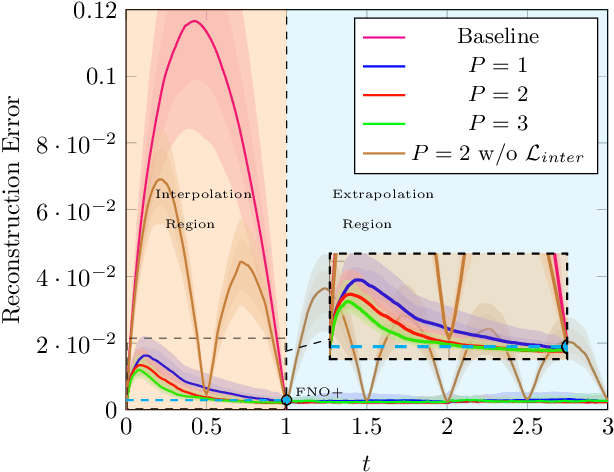
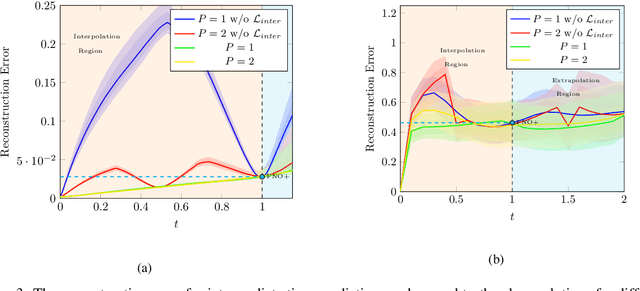
The evolution of dynamical systems is generically governed by nonlinear partial differential equations (PDEs), whose solution, in a simulation framework, requires vast amounts of computational resources. In this work, we present a novel method that combines a hyper-network solver with a Fourier Neural Operator architecture. Our method treats time and space separately. As a result, it successfully propagates initial conditions in continuous time steps by employing the general composition properties of the partial differential operators. Following previous work, supervision is provided at a specific time point. We test our method on various time evolution PDEs, including nonlinear fluid flows in one, two, and three spatial dimensions. The results show that the new method improves the learning accuracy at the time point of supervision point, and is able to interpolate and the solutions to any intermediate time.

Unsupervised Disentanglement with Tensor Product Representations on the Torus

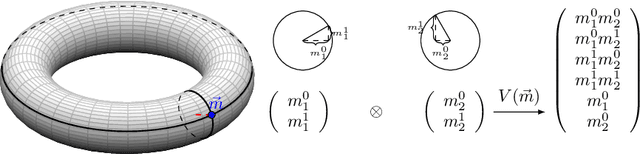
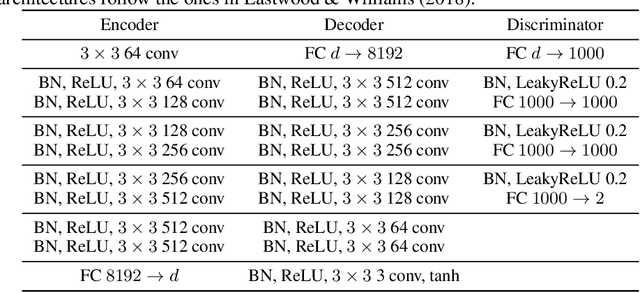
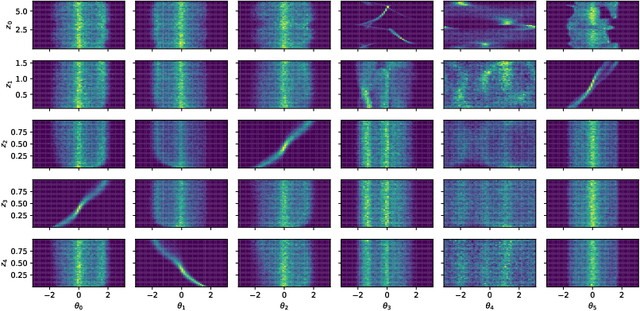
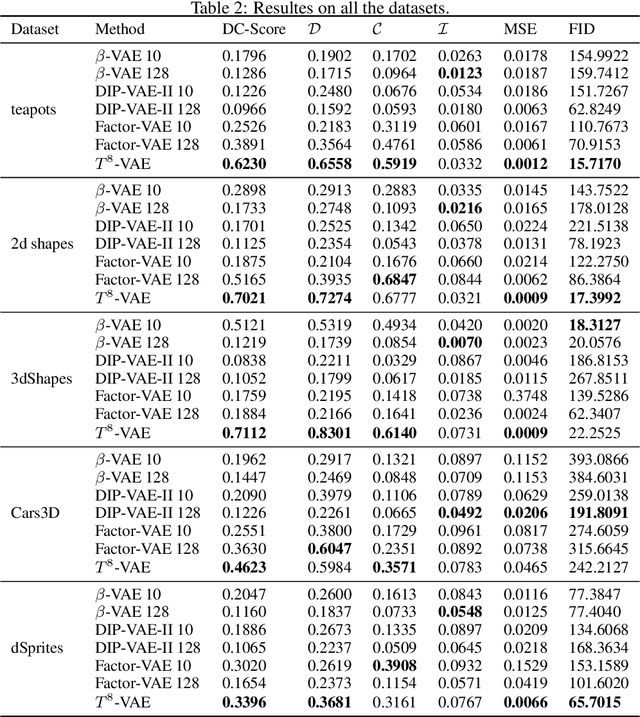
The current methods for learning representations with auto-encoders almost exclusively employ vectors as the latent representations. In this work, we propose to employ a tensor product structure for this purpose. This way, the obtained representations are naturally disentangled. In contrast to the conventional variations methods, which are targeted toward normally distributed features, the latent space in our representation is distributed uniformly over a set of unit circles. We argue that the torus structure of the latent space captures the generative factors effectively. We employ recent tools for measuring unsupervised disentanglement, and in an extensive set of experiments demonstrate the advantage of our method in terms of disentanglement, completeness, and informativeness. The code for our proposed method is available at https://github.com/rotmanmi/Unsupervised-Disentanglement-Torus.

Entanglement Diagnostics for Efficient Quantum Computation

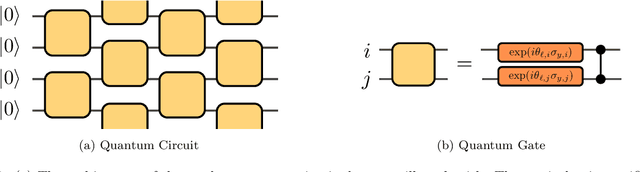
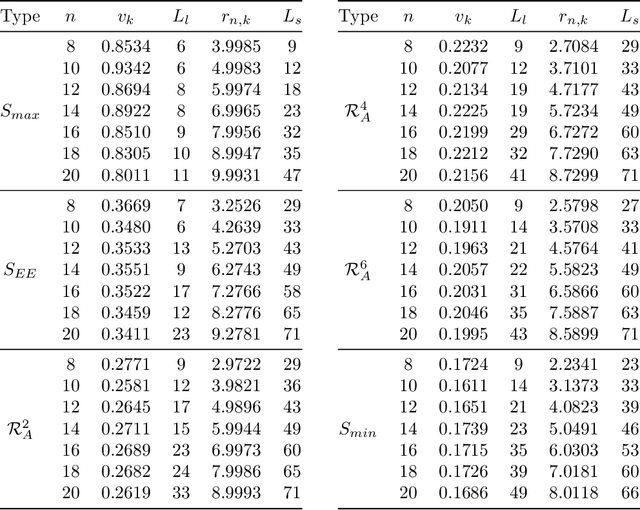
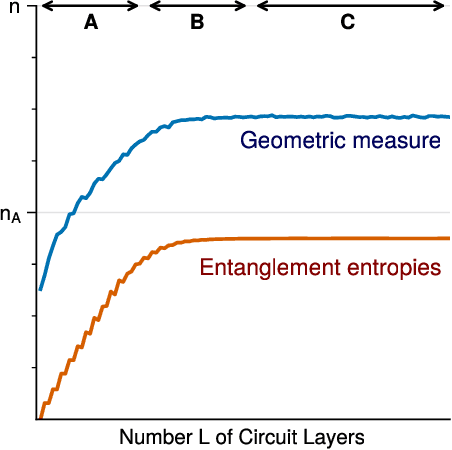
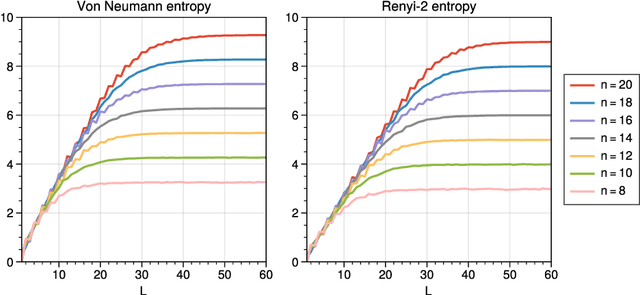
We consider information spreading measures in randomly initialized variational quantum circuits and construct entanglement diagnostics for efficient quantum/classical hybrid computations. Following the Renyi entropies of the random circuit's reduced density matrix, we divide the number of circuit layers into two separate regions with a transitioning zone between them. We identify the high-performance region for solving optimization problems encoded in the cost function of k-local Hamiltonians. We consider three example Hamiltonians, i.e., the nearest-neighbor transverse-field Ising model, the long-range transverse-field Ising model and the Sachdev-Ye-Kitaev model. By analyzing the qualitative and quantitative differences in the respective optimization processes, we demonstrate that the entanglement measures are robust diagnostics that are highly correlated with the optimization performance. We study the advantage of entanglement diagnostics for different circuit architectures and the impact of changing the parameter space dimensionality while maintaining its entanglement structure.