Semi-supervised Learning of Partial Differential Operators and Dynamical Flows
Paper and Code
Jul 28, 2022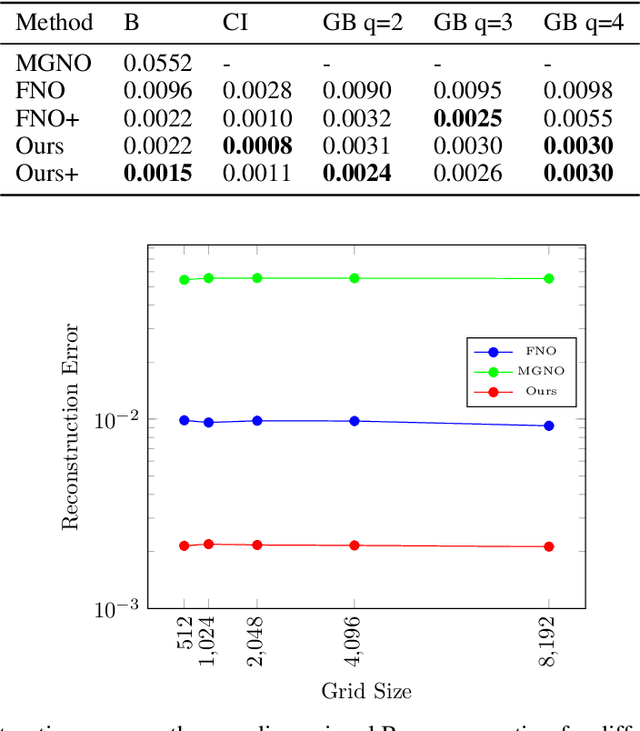
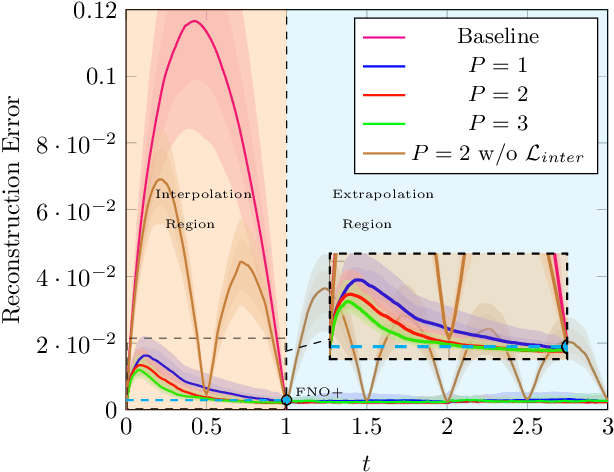

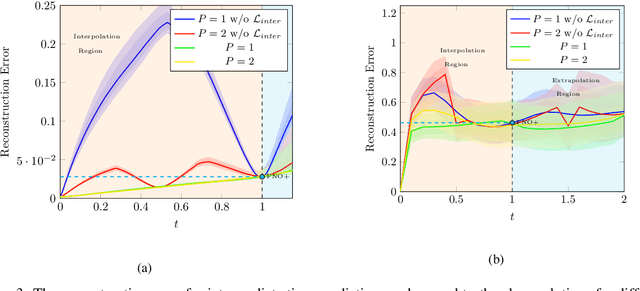
The evolution of dynamical systems is generically governed by nonlinear partial differential equations (PDEs), whose solution, in a simulation framework, requires vast amounts of computational resources. In this work, we present a novel method that combines a hyper-network solver with a Fourier Neural Operator architecture. Our method treats time and space separately. As a result, it successfully propagates initial conditions in continuous time steps by employing the general composition properties of the partial differential operators. Following previous work, supervision is provided at a specific time point. We test our method on various time evolution PDEs, including nonlinear fluid flows in one, two, and three spatial dimensions. The results show that the new method improves the learning accuracy at the time point of supervision point, and is able to interpolate and the solutions to any intermediate time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge