Joonho Kim
Entanglement Diagnostics for Efficient Quantum Computation
Feb 24, 2021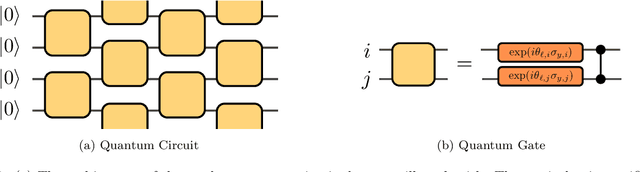
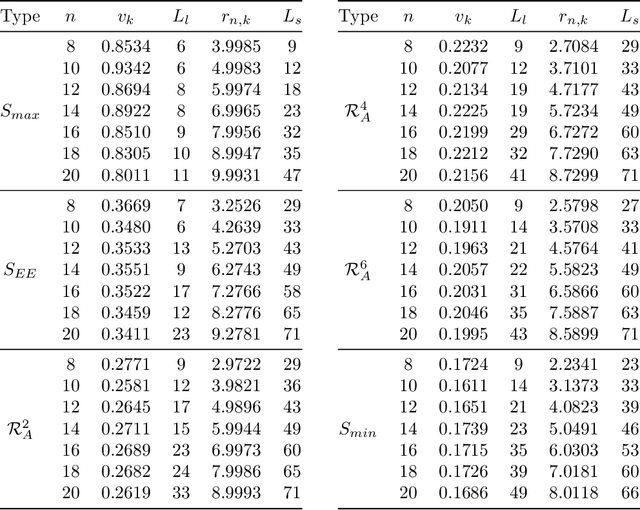
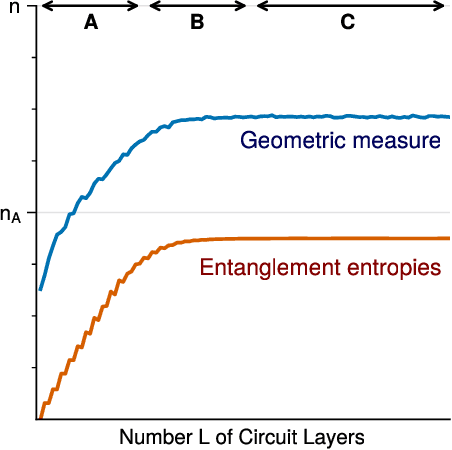
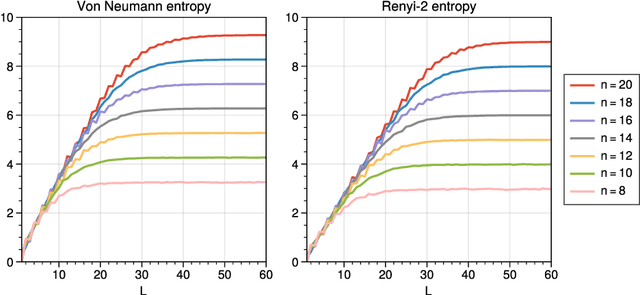
Abstract:We consider information spreading measures in randomly initialized variational quantum circuits and construct entanglement diagnostics for efficient quantum/classical hybrid computations. Following the Renyi entropies of the random circuit's reduced density matrix, we divide the number of circuit layers into two separate regions with a transitioning zone between them. We identify the high-performance region for solving optimization problems encoded in the cost function of k-local Hamiltonians. We consider three example Hamiltonians, i.e., the nearest-neighbor transverse-field Ising model, the long-range transverse-field Ising model and the Sachdev-Ye-Kitaev model. By analyzing the qualitative and quantitative differences in the respective optimization processes, we demonstrate that the entanglement measures are robust diagnostics that are highly correlated with the optimization performance. We study the advantage of entanglement diagnostics for different circuit architectures and the impact of changing the parameter space dimensionality while maintaining its entanglement structure.
Universal Effectiveness of High-Depth Circuits in Variational Eigenproblems
Oct 01, 2020



Abstract:We explore the effectiveness of high-depth, noiseless, parameteric quantum circuits by challenging their capability to simulate the ground states of quantum many-body Hamiltonians. Even a generic layered circuit Ansatz can approximate the ground state with high precision, as long as the circuit depth exceeds a certain threshold level that exponentially scales with the number of qubits, despite the abundance of the barren plateaus. This success is due to the fact that the energy landscape in the high-depth regime has a suitable structure for the gradient-based optimization, i.e., the presence of local extrema -- near any random initial points -- reaching the ground level energy. We check if these advantages are preserved across different Hamiltonians, by working out two variational eigensolver problems for the transverse field Ising model as well as for the Sachdev-Ye-Kitaev model. We expect that the contributing factors to the universal success of the high-depth circuits may also serve as the evaluation guidelines for more realistic circuit designs under hybrid quantum-classical algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge