Entanglement Diagnostics for Efficient Quantum Computation

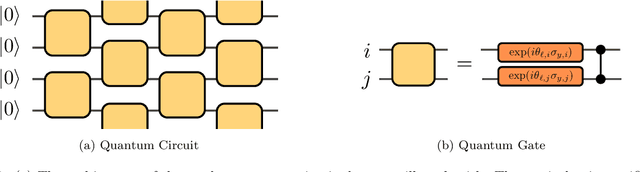
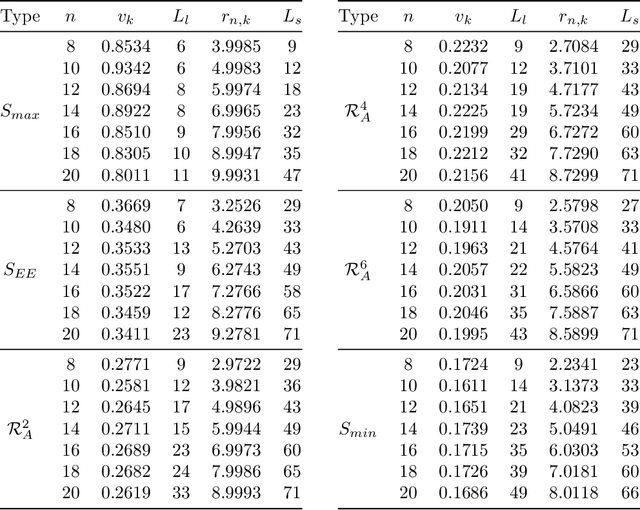
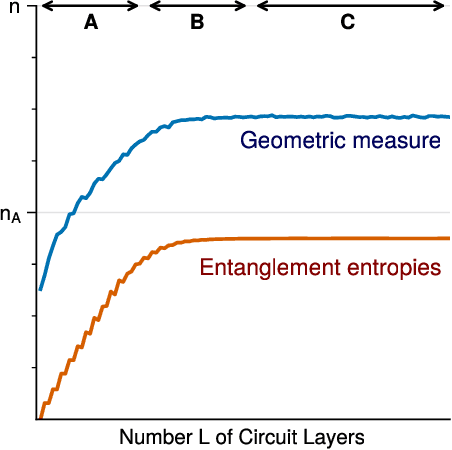
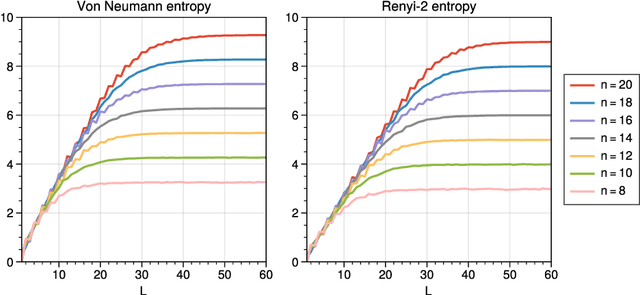
We consider information spreading measures in randomly initialized variational quantum circuits and construct entanglement diagnostics for efficient quantum/classical hybrid computations. Following the Renyi entropies of the random circuit's reduced density matrix, we divide the number of circuit layers into two separate regions with a transitioning zone between them. We identify the high-performance region for solving optimization problems encoded in the cost function of k-local Hamiltonians. We consider three example Hamiltonians, i.e., the nearest-neighbor transverse-field Ising model, the long-range transverse-field Ising model and the Sachdev-Ye-Kitaev model. By analyzing the qualitative and quantitative differences in the respective optimization processes, we demonstrate that the entanglement measures are robust diagnostics that are highly correlated with the optimization performance. We study the advantage of entanglement diagnostics for different circuit architectures and the impact of changing the parameter space dimensionality while maintaining its entanglement structure.