Turbulence Scaling from Deep Learning Diffusion Generative Models

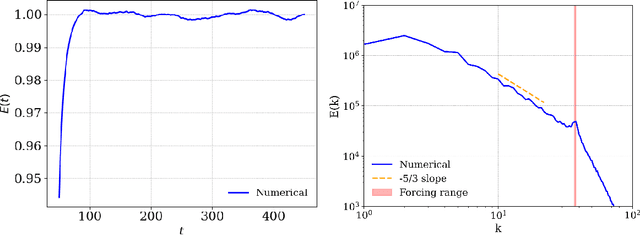
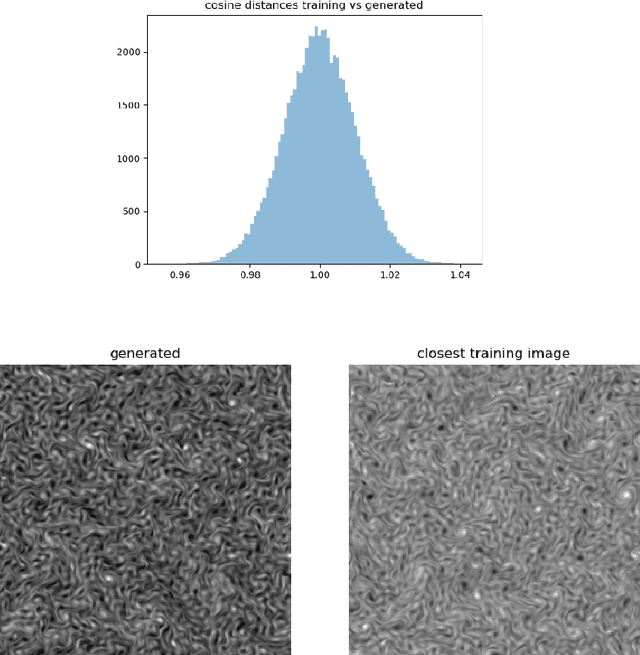
Complex spatial and temporal structures are inherent characteristics of turbulent fluid flows and comprehending them poses a major challenge. This comprehesion necessitates an understanding of the space of turbulent fluid flow configurations. We employ a diffusion-based generative model to learn the distribution of turbulent vorticity profiles and generate snapshots of turbulent solutions to the incompressible Navier-Stokes equations. We consider the inverse cascade in two spatial dimensions and generate diverse turbulent solutions that differ from those in the training dataset. We analyze the statistical scaling properties of the new turbulent profiles, calculate their structure functions, energy power spectrum, velocity probability distribution function and moments of local energy dissipation. All the learnt scaling exponents are consistent with the expected Kolmogorov scaling and have lower errors than the training ones. This agreement with established turbulence characteristics provides strong evidence of the model's capability to capture essential features of real-world turbulence.

Aspects of human memory and Large Language Models

Large Language Models (LLMs) are huge artificial neural networks which primarily serve to generate text, but also provide a very sophisticated probabilistic model of language use. Since generating a semantically consistent text requires a form of effective memory, we investigate the memory properties of LLMs and find surprising similarities with key characteristics of human memory. We argue that the human-like memory properties of the Large Language Model do not follow automatically from the LLM architecture but are rather learned from the statistics of the training textual data. These results strongly suggest that the biological features of human memory leave an imprint on the way that we structure our textual narratives.

Neural Network Complexity of Chaos and Turbulence

We study the complexity of chaos and turbulence as viewed by deep neural networks by considering network classification tasks of distinguishing turbulent from chaotic fluid flows, noise and real world images of cats or dogs. We analyze the relative difficulty of these classification tasks and quantify the complexity of the computation at the intermediate and final stages. We analyze incompressible as well as weakly compressible fluid flows and provide evidence for the feature identified by the neural network to distinguish turbulence from chaos.

Aesthetics and neural network image representations

We analyze the spaces of images encoded by generative networks of the BigGAN architecture. We find that generic multiplicative perturbations away from the photo-realistic point often lead to images which appear as "artistic renditions" of the corresponding objects. This demonstrates an emergence of aesthetic properties directly from the structure of the photo-realistic environment coupled with its neural network parametrization. Moreover, modifying a deep semantic part of the neural network encoding leads to the appearance of symbolic visual representations.

Neural networks adapting to datasets: learning network size and topology

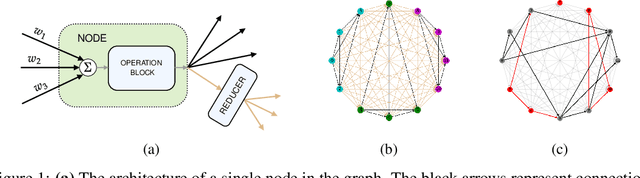
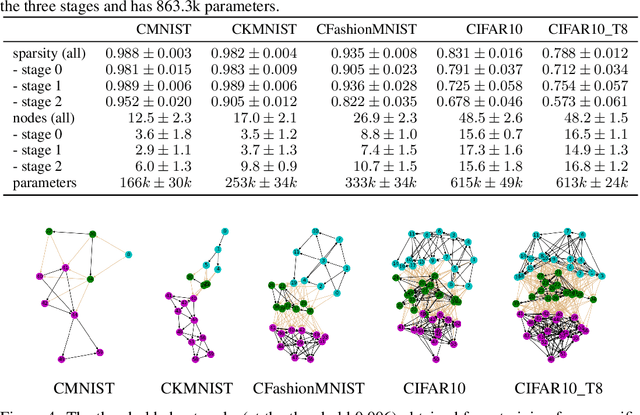
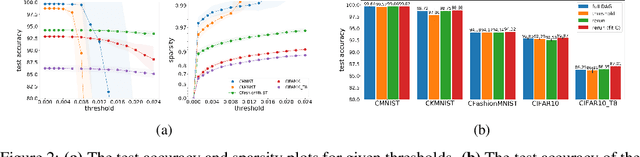
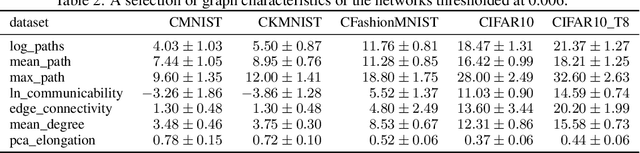
We introduce a flexible setup allowing for a neural network to learn both its size and topology during the course of a standard gradient-based training. The resulting network has the structure of a graph tailored to the particular learning task and dataset. The obtained networks can also be trained from scratch and achieve virtually identical performance. We explore the properties of the network architectures for a number of datasets of varying difficulty observing systematic regularities. The obtained graphs can be therefore understood as encoding nontrivial characteristics of the particular classification tasks.

Complexity for deep neural networks and other characteristics of deep feature representations

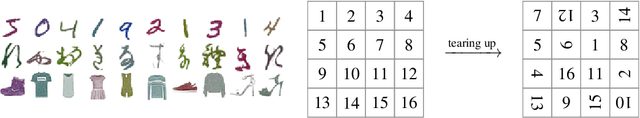
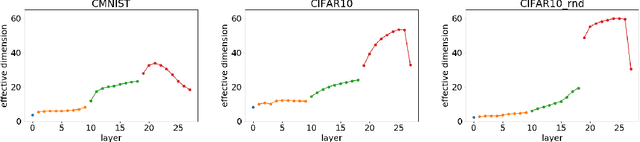
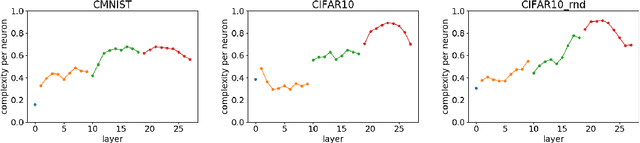
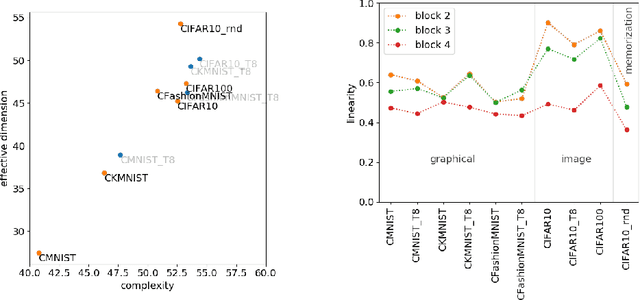
We define a notion of complexity, motivated by considerations of circuit complexity, which quantifies the nonlinearity of the computation of a neural network, as well as a complementary measure of the effective dimension of feature representations. We investigate these observables both for trained networks for various datasets as well as explore their dynamics during training. These observables can be understood in a dual way as uncovering hidden internal structure of the datasets themselves as a function of scale or depth. The entropic character of the proposed notion of complexity should allow to transfer modes of analysis from neuroscience and statistical physics to the domain of artificial neural networks.

Neural Networks on Random Graphs

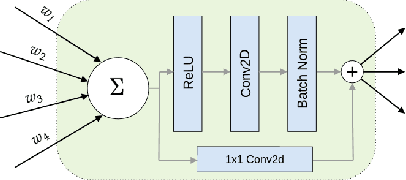
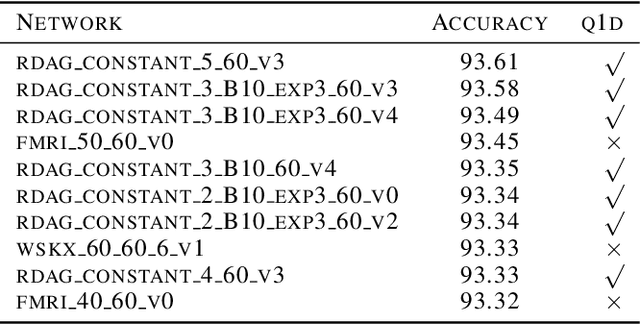
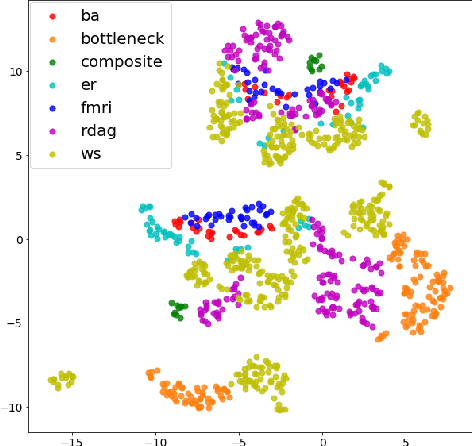
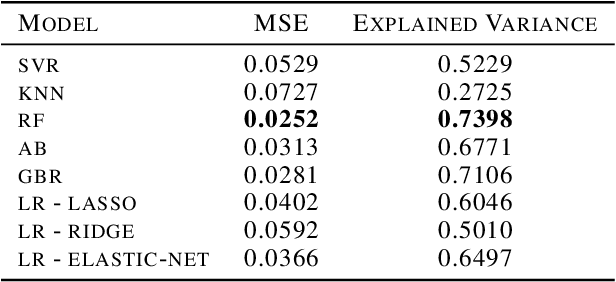
We performed a massive evaluation of neural networks with architectures corresponding to random graphs of various types. Apart from the classical random graph families including random, scale-free and small world graphs, we introduced a novel and flexible algorithm for directly generating random directed acyclic graphs (DAG) and studied a class of graphs derived from functional resting state fMRI networks. A majority of the best performing networks were indeed in these new families. We also proposed a general procedure for turning a graph into a DAG necessary for a feed-forward neural network. We investigated various structural and numerical properties of the graphs in relation to neural network test accuracy. Since none of the classical numerical graph invariants by itself seems to allow to single out the best networks, we introduced new numerical characteristics that selected a set of quasi-1-dimensional graphs, which were the majority among the best performing networks.

Entropy from Machine Learning

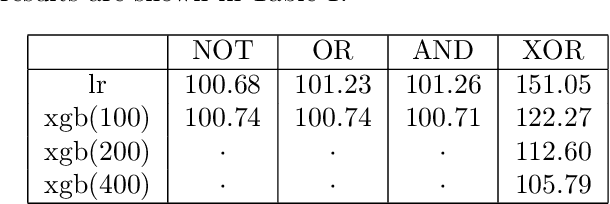
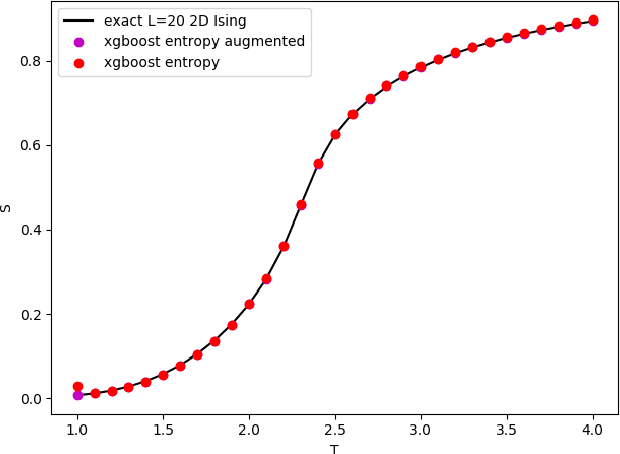
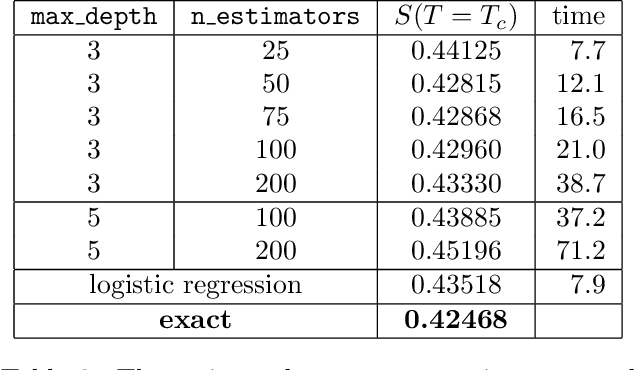
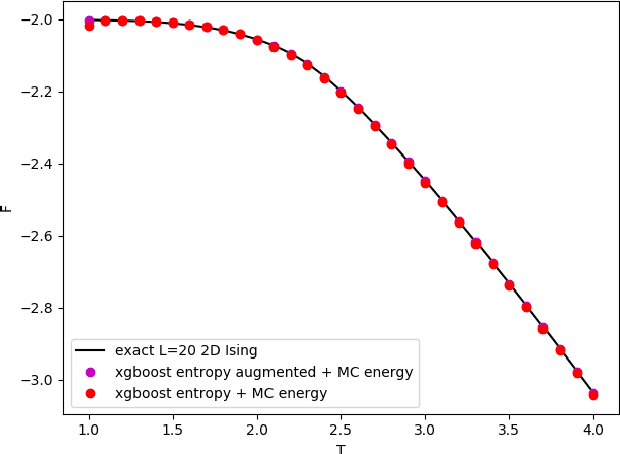
We translate the problem of calculating the entropy of a set of binary configurations/signals into a sequence of supervised classification tasks. Subsequently, one can use virtually any machine learning classification algorithm for computing entropy. This procedure can be used to compute entropy, and consequently the free energy directly from a set of Monte Carlo configurations at a given temperature. As a test of the proposed method, using an off-the-shelf machine learning classifier we reproduce the entropy and free energy of the 2D Ising model from Monte Carlo configurations at various temperatures throughout its phase diagram. Other potential applications include computing the entropy of spiking neurons or any other multidimensional binary signals.