Complexity for deep neural networks and other characteristics of deep feature representations
Paper and Code
Jun 08, 2020
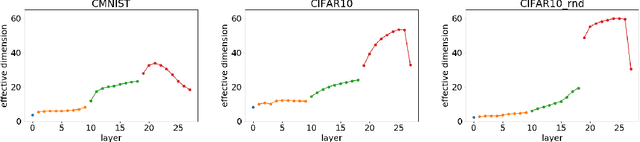
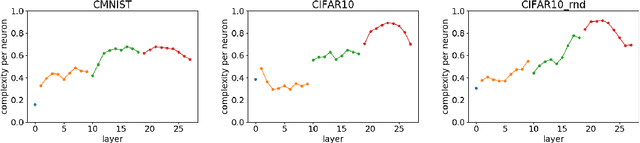
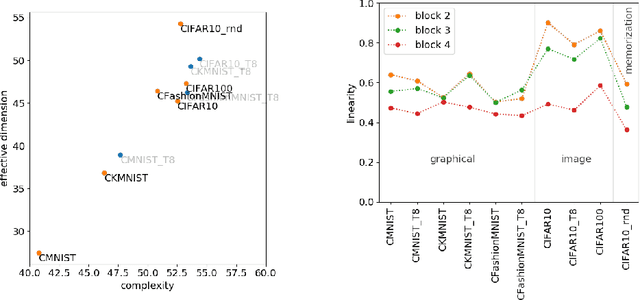
We define a notion of complexity, motivated by considerations of circuit complexity, which quantifies the nonlinearity of the computation of a neural network, as well as a complementary measure of the effective dimension of feature representations. We investigate these observables both for trained networks for various datasets as well as explore their dynamics during training. These observables can be understood in a dual way as uncovering hidden internal structure of the datasets themselves as a function of scale or depth. The entropic character of the proposed notion of complexity should allow to transfer modes of analysis from neuroscience and statistical physics to the domain of artificial neural networks.
* 8 pages + 6 supplementary pages, 7+7 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge