Trust Your $ abla$: Gradient-based Intervention Targeting for Causal Discovery

Inferring causal structure from data is a challenging task of fundamental importance in science. Observational data are often insufficient to identify a system's causal structure uniquely. While conducting interventions (i.e., experiments) can improve the identifiability, such samples are usually challenging and expensive to obtain. Hence, experimental design approaches for causal discovery aim to minimize the number of interventions by estimating the most informative intervention target. In this work, we propose a novel Gradient-based Intervention Targeting method, abbreviated GIT, that 'trusts' the gradient estimator of a gradient-based causal discovery framework to provide signals for the intervention acquisition function. We provide extensive experiments in simulated and real-world datasets and demonstrate that GIT performs on par with competitive baselines, surpassing them in the low-data regime.

Non-Gaussian Gaussian Processes for Few-Shot Regression

Gaussian Processes (GPs) have been widely used in machine learning to model distributions over functions, with applications including multi-modal regression, time-series prediction, and few-shot learning. GPs are particularly useful in the last application since they rely on Normal distributions and enable closed-form computation of the posterior probability function. Unfortunately, because the resulting posterior is not flexible enough to capture complex distributions, GPs assume high similarity between subsequent tasks - a requirement rarely met in real-world conditions. In this work, we address this limitation by leveraging the flexibility of Normalizing Flows to modulate the posterior predictive distribution of the GP. This makes the GP posterior locally non-Gaussian, therefore we name our method Non-Gaussian Gaussian Processes (NGGPs). More precisely, we propose an invertible ODE-based mapping that operates on each component of the random variable vectors and shares the parameters across all of them. We empirically tested the flexibility of NGGPs on various few-shot learning regression datasets, showing that the mapping can incorporate context embedding information to model different noise levels for periodic functions. As a result, our method shares the structure of the problem between subsequent tasks, but the contextualization allows for adaptation to dissimilarities. NGGPs outperform the competing state-of-the-art approaches on a diversified set of benchmarks and applications.

On the relationship between disentanglement and multi-task learning

One of the main arguments behind studying disentangled representations is the assumption that they can be easily reused in different tasks. At the same time finding a joint, adaptable representation of data is one of the key challenges in the multi-task learning setting. In this paper, we take a closer look at the relationship between disentanglement and multi-task learning based on hard parameter sharing. We perform a thorough empirical study of the representations obtained by neural networks trained on automatically generated supervised tasks. Using a set of standard metrics we show that disentanglement appears naturally during the process of multi-task neural network training.

Neural networks adapting to datasets: learning network size and topology

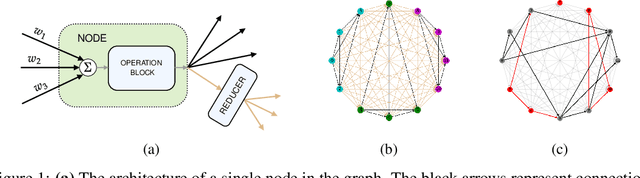
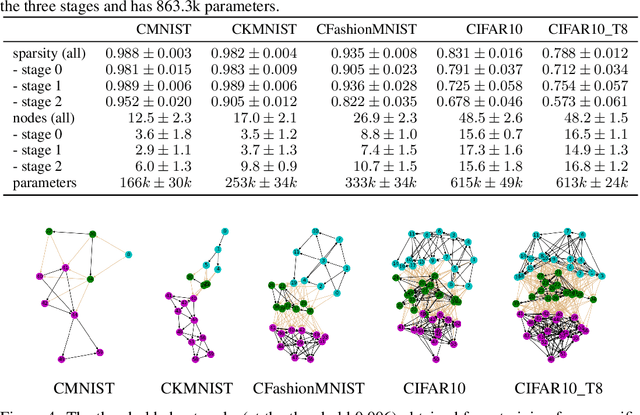
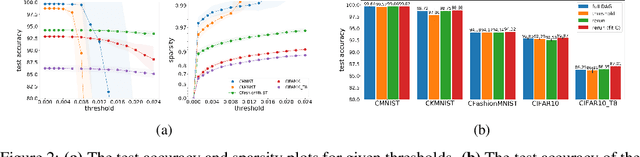
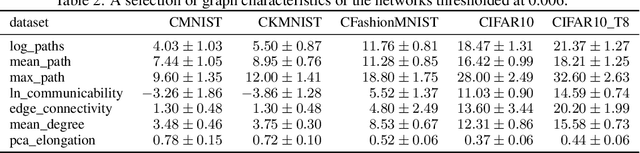
We introduce a flexible setup allowing for a neural network to learn both its size and topology during the course of a standard gradient-based training. The resulting network has the structure of a graph tailored to the particular learning task and dataset. The obtained networks can also be trained from scratch and achieve virtually identical performance. We explore the properties of the network architectures for a number of datasets of varying difficulty observing systematic regularities. The obtained graphs can be therefore understood as encoding nontrivial characteristics of the particular classification tasks.

Neural Networks on Random Graphs

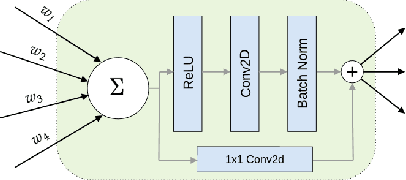
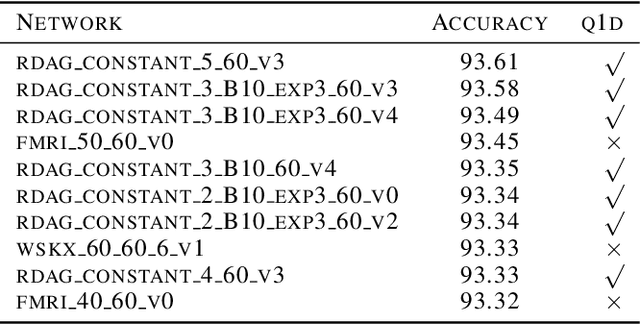
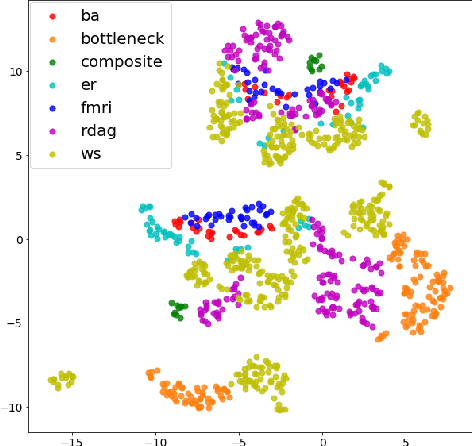
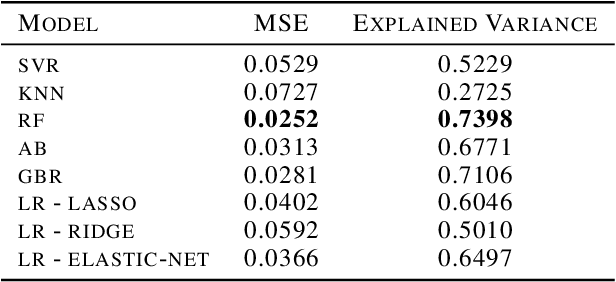
We performed a massive evaluation of neural networks with architectures corresponding to random graphs of various types. Apart from the classical random graph families including random, scale-free and small world graphs, we introduced a novel and flexible algorithm for directly generating random directed acyclic graphs (DAG) and studied a class of graphs derived from functional resting state fMRI networks. A majority of the best performing networks were indeed in these new families. We also proposed a general procedure for turning a graph into a DAG necessary for a feed-forward neural network. We investigated various structural and numerical properties of the graphs in relation to neural network test accuracy. Since none of the classical numerical graph invariants by itself seems to allow to single out the best networks, we introduced new numerical characteristics that selected a set of quasi-1-dimensional graphs, which were the majority among the best performing networks.

WICA: nonlinear weighted ICA

Independent Component Analysis (ICA) aims to find a coordinate system in which the components of the data are independent. In this paper we construct a new nonlinear ICA model, called WICA, which obtains better and more stable results than other algorithms. A crucial tool is given by a new efficient method of verifying nonlinear dependence with the use of computation of correlation coefficients for normally weighted data.

Interpolation in generative models

We show how to construct smooth and realistic interpolations for generative models, with arbitrary, not necessarily Gaussian, prior. The crucial idea is based on the construction on the realisticity index of a curve, which maximisation, as we show, leads to a search of a geodesic with respect to the corresponding Riemann structure.

Non-linear ICA based on Cramer-Wold metric

Non-linear source separation is a challenging open problem with many applications. We extend a recently proposed Adversarial Non-linear ICA (ANICA) model, and introduce Cramer-Wold ICA (CW-ICA). In contrast to ANICA we use a simple, closed--form optimization target instead of a discriminator--based independence measure. Our results show that CW-ICA achieves comparable results to ANICA, while foregoing the need for adversarial training.

Deep processing of structured data

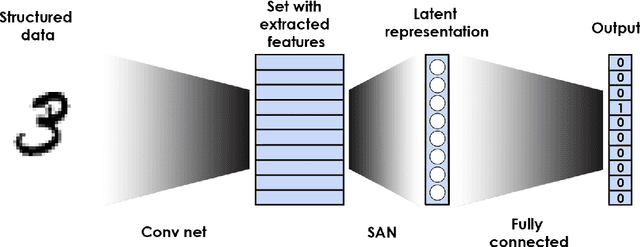
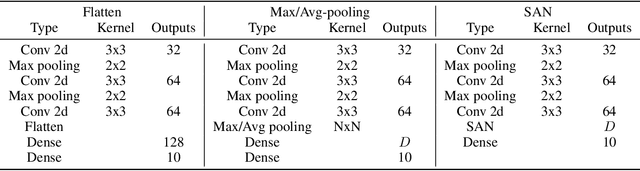
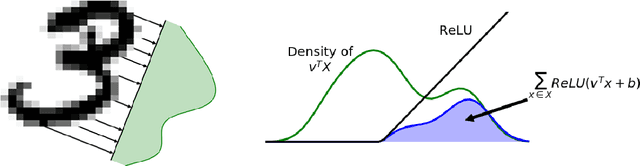
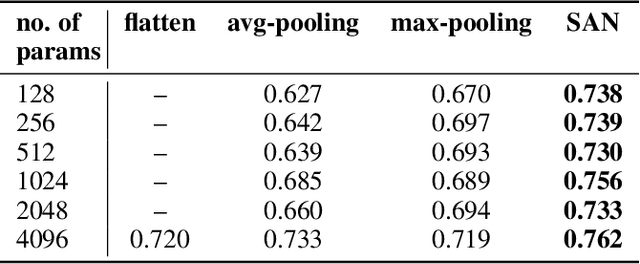
We construct a general unified framework for learning representation of structured data, i.e. data which cannot be represented as the fixed-length vectors (e.g. sets, graphs, texts or images of varying sizes). The key factor is played by an intermediate network called SAN (Set Aggregating Network), which maps a structured object to a fixed length vector in a high dimensional latent space. Our main theoretical result shows that for sufficiently large dimension of the latent space, SAN is capable of learning a unique representation for every input example. Experiments demonstrate that replacing pooling operation by SAN in convolutional networks leads to better results in classifying images with different sizes. Moreover, its direct application to text and graph data allows to obtain results close to SOTA, by simpler networks with smaller number of parameters than competitive models.